15 Of 460
stanleys
Sep 15, 2025 · 5 min read
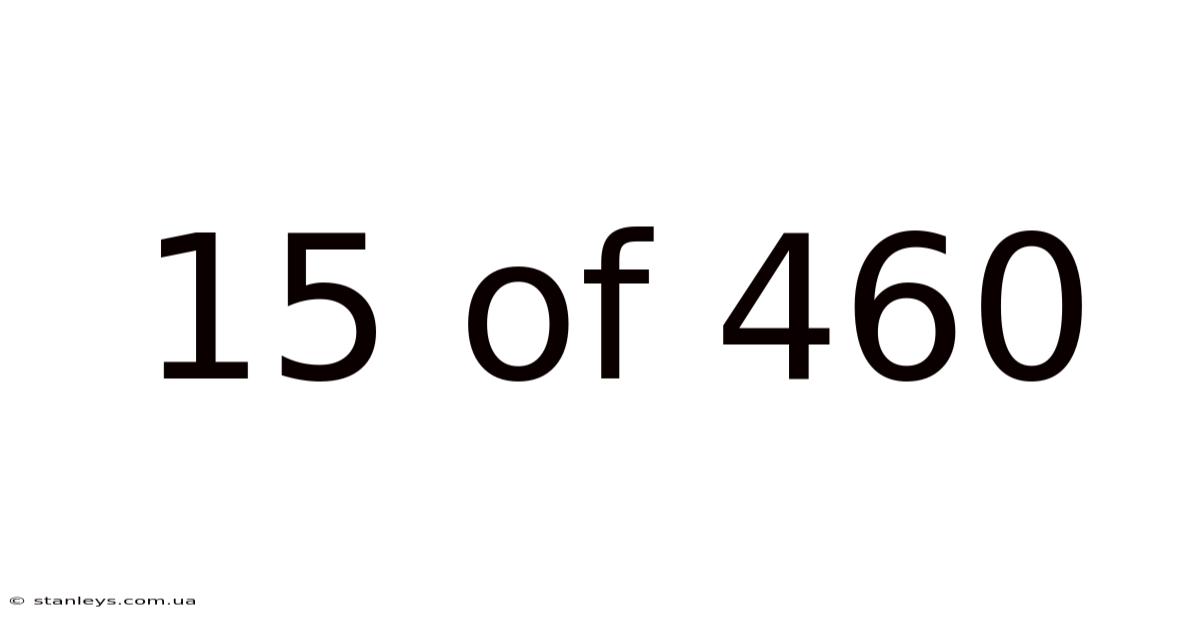
Table of Contents
Decoding the Enigma: Understanding the Fraction 15/460 and its Implications
The seemingly simple fraction 15/460 might initially appear unremarkable. However, a deeper dive reveals a wealth of mathematical concepts and practical applications that extend beyond basic arithmetic. This article will explore the multifaceted nature of 15/460, examining its simplification, decimal representation, percentage equivalent, applications in various fields, and its relevance in understanding broader mathematical principles. We'll also touch upon common misconceptions and provide helpful tips for working with similar fractions.
Understanding the Basics: Simplifying 15/460
The first step in understanding any fraction is to simplify it to its lowest terms. This involves finding the greatest common divisor (GCD) of the numerator (15) and the denominator (460) and dividing both by it. Let's break it down:
-
Finding the GCD: The factors of 15 are 1, 3, 5, and 15. The factors of 460 are 1, 2, 4, 5, 10, 20, 23, 46, 92, 115, 230, and 460. The greatest common factor shared by both is 5.
-
Simplifying the Fraction: Dividing both the numerator and denominator by 5, we get: 15 ÷ 5 = 3 and 460 ÷ 5 = 92. Therefore, the simplified form of 15/460 is 3/92.
This simplified fraction is easier to work with and represents the same proportional value as the original fraction. It's crucial to simplify fractions whenever possible to improve clarity and ease of calculation.
From Fraction to Decimal: The Decimal Representation of 3/92
Converting a fraction to its decimal equivalent involves dividing the numerator by the denominator. In this case, we divide 3 by 92:
3 ÷ 92 ≈ 0.03260869565...
Notice that the decimal representation is non-terminating and non-repeating. This means it continues infinitely without a repeating pattern of digits. This is characteristic of many fractions where the denominator has prime factors other than 2 and 5. In practical applications, we often round the decimal to a specific number of decimal places based on the required level of precision. For example, we might round 3/92 to 0.033 or 0.0326.
Percentage Equivalence: Expressing 3/92 as a Percentage
To express the fraction 3/92 as a percentage, we multiply the decimal equivalent by 100:
0.03260869565... × 100 ≈ 3.26%
This percentage representation provides a readily understandable way to communicate the proportional value of the fraction. For instance, if 3 out of 92 students passed an exam, we could say that approximately 3.26% of the students passed.
Real-World Applications: Where 15/460 (or 3/92) Might Appear
While seemingly insignificant, fractions like 3/92 appear in various real-world contexts. Consider these examples:
-
Probability and Statistics: Imagine a scenario involving a probability experiment with 92 equally likely outcomes, where 3 outcomes correspond to a specific event. The probability of that event occurring would be 3/92 or approximately 3.26%.
-
Surveys and Sampling: In a survey of 92 people, if 3 responded in a particular way, the proportion responding in that way would be 3/92.
-
Financial Calculations: Fractions are frequently used in financial calculations, such as determining proportions of investments or calculating interest rates. Although 3/92 might not be a common interest rate, it illustrates the principle of using fractions in financial contexts.
-
Engineering and Measurement: Precise measurements in engineering often involve fractions. While 3/92 might not be a typical measurement value, it demonstrates the general principle of using fractions to represent proportions in various scales.
-
Recipes and Cooking: Scaling down or up recipes might involve adjusting ingredient quantities based on fractions.
Beyond the Basics: Exploring Related Mathematical Concepts
Understanding 15/460 (or its simplified form 3/92) provides a foundation for exploring several broader mathematical concepts:
-
Ratio and Proportion: Fractions represent ratios, expressing the relationship between two quantities. The ratio 3:92 indicates that for every 3 units of one quantity, there are 92 units of another.
-
Rational Numbers: Fractions like 3/92 are rational numbers, meaning they can be expressed as the ratio of two integers. This contrasts with irrational numbers, such as π (pi) or √2, which cannot be expressed as a simple fraction.
-
Continued Fractions: Any rational number can be represented as a continued fraction. While the continued fraction representation of 3/92 might be less intuitive than its simple fractional form, it showcases another way to express rational numbers.
-
Approximation and Rounding: When working with decimals, it's often necessary to round the numbers to a certain level of accuracy. Understanding the implications of rounding is crucial for maintaining the integrity of calculations.
Frequently Asked Questions (FAQ)
Q: Why is simplifying fractions important?
A: Simplifying fractions makes them easier to work with, improves clarity, and reduces the likelihood of errors in calculations. It represents the same proportional value in a more concise form.
Q: How can I convert a fraction to a decimal?
A: Divide the numerator by the denominator. Use a calculator if needed.
Q: How can I convert a fraction to a percentage?
A: Convert the fraction to a decimal and then multiply by 100.
Q: What if the fraction has a larger numerator than denominator?
A: If the numerator is larger than the denominator, the fraction is an improper fraction. You can convert it to a mixed number (a whole number and a proper fraction) by performing the division and expressing the remainder as a fraction.
Q: Are there any online tools to help with fraction calculations?
A: Yes, many online calculators and websites are available to assist with fraction simplification, conversion, and other calculations.
Conclusion: The Significance of Seemingly Small Fractions
While the fraction 15/460 might seem insignificant at first glance, a closer examination reveals its importance within the broader context of mathematics and its application in various fields. Understanding its simplification, decimal and percentage equivalents, and its potential real-world applications highlights the crucial role of fractions in representing proportions and solving practical problems. Mastering fraction manipulation is a fundamental skill that extends far beyond basic arithmetic, underpinning more advanced mathematical concepts and real-world problem-solving. Remember, even seemingly small fractions like 3/92 hold significant mathematical meaning and practical relevance. The key is to understand the underlying principles and apply them effectively.
Latest Posts
Latest Posts
-
3 4 Of 48
Sep 15, 2025
-
Perception Vs Perspective
Sep 15, 2025
-
82f In C
Sep 15, 2025
-
33 X 5
Sep 15, 2025
-
33 X 4
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 15 Of 460 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.