33 X 5
stanleys
Sep 15, 2025 · 5 min read
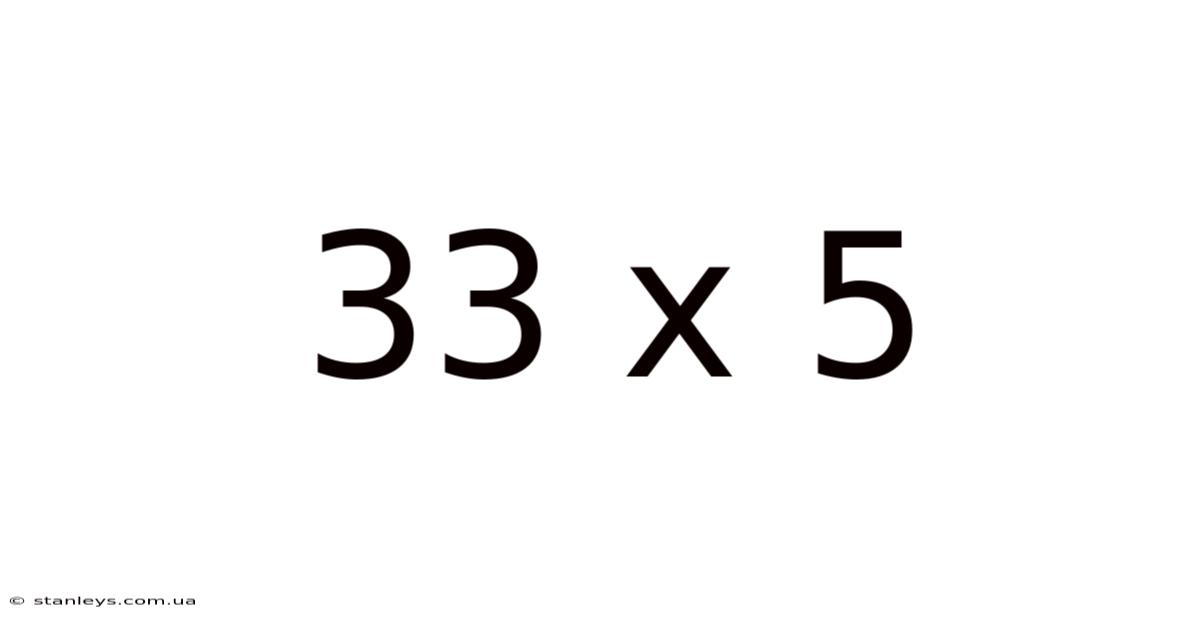
Table of Contents
Exploring the Multiplication Problem: 33 x 5 – A Deep Dive into Methods and Applications
This article delves into the seemingly simple multiplication problem, 33 x 5. While the answer might seem readily apparent, we'll unpack various methods for solving it, exploring the underlying mathematical principles and showcasing its relevance in different contexts. This journey will not only solidify your understanding of basic arithmetic but also highlight the broader applications of multiplication in everyday life and advanced mathematics. This exploration will cover different approaches, from basic multiplication techniques to more advanced methods, and will also touch upon real-world applications of this simple calculation.
Understanding the Fundamentals: What is Multiplication?
Multiplication, at its core, is repeated addition. When we say 33 x 5, we are essentially adding 33 to itself five times: 33 + 33 + 33 + 33 + 33. This fundamental understanding is crucial, especially for grasping the concept for beginners. It lays the groundwork for more complex mathematical operations.
While the concept is simple, its applications are vast. From calculating the total cost of multiple items to determining the area of a rectangle, multiplication is an indispensable tool across numerous disciplines.
Method 1: The Standard Algorithm
The standard algorithm is the most commonly taught method for multiplication. It involves multiplying each digit of the multiplicand (33) by each digit of the multiplier (5), then adding the results.
Here's how it works for 33 x 5:
- Multiply the ones digit: 5 x 3 = 15. Write down the '5' and carry-over the '1'.
- Multiply the tens digit: 5 x 3 = 15. Add the carried-over '1': 15 + 1 = 16. Write down '16'.
- Combine the results: The final answer is 165.
This method is efficient and systematic, making it a cornerstone of elementary mathematics education.
Method 2: Distributive Property
The distributive property of multiplication over addition states that a(b + c) = ab + ac. We can use this property to break down the problem into smaller, more manageable parts:
33 x 5 = 30 x 5 + 3 x 5 = 150 + 15 = 165
This method helps to illustrate the underlying principles of multiplication and can be particularly helpful in mental math calculations. Breaking down larger numbers into simpler components makes multiplication easier to perform without relying on written calculations.
Method 3: Repeated Addition
As mentioned earlier, multiplication is simply repeated addition. Therefore, we can solve 33 x 5 by adding 33 five times:
33 + 33 + 33 + 33 + 33 = 165
While this method is straightforward, it becomes less efficient for larger numbers. However, it's a valuable approach for reinforcing the fundamental concept of multiplication for younger learners. Visually representing this process, perhaps using objects or drawings, can be a very effective teaching strategy.
Method 4: Using Arrays
Visual learners often benefit from representing multiplication problems using arrays. An array is a rectangular arrangement of objects in rows and columns. For 33 x 5, we can create an array with 33 objects in each of five rows. Counting all the objects will give the answer, 165. This method is excellent for demonstrating the concrete relationship between multiplication and area.
Method 5: Mental Math Techniques
With practice, you can perform 33 x 5 mentally using various strategies. One approach is to double and halve:
- Double 33: 66
- Halve 5: 2.5
- 66 x 2.5 is more challenging mentally, but we can further break it down: 66 x 2 + 66 x 0.5 = 132 + 33 = 165
Alternatively, you can round and adjust:
- Approximate 33 as 30. 30 x 5 = 150.
- Add the difference: 3 x 5 = 15.
- 150 + 15 = 165
Mental math techniques are valuable for quick calculations and improve numerical fluency.
Real-World Applications of 33 x 5
While seemingly simple, the multiplication of 33 x 5 has practical applications in various real-world scenarios:
- Retail: Calculating the total cost of 5 items priced at $33 each.
- Inventory: Determining the total number of items if there are 33 items in 5 boxes.
- Construction: Calculating the total length of 5 pieces of wood, each 33 centimeters long.
- Baking: Calculating the total amount of an ingredient needed if each recipe requires 33 grams and you're making 5 recipes.
- Gardening: Determining the total number of plants if you have 5 rows with 33 plants in each row.
Extending the Concept: Larger Multiplications
Understanding 33 x 5 provides a solid foundation for tackling more complex multiplication problems. The principles and methods discussed here, like the distributive property and breaking down numbers, can be applied to larger numbers and even algebraic expressions. This understanding will help students grasp the concept of multiplication in various contexts.
Frequently Asked Questions (FAQ)
-
Q: What is the easiest way to solve 33 x 5?
- A: The standard algorithm is generally the easiest and most widely taught method. However, the best method depends on individual preference and understanding. The distributive property or repeated addition can also be effective.
-
Q: Why is learning multiplication important?
- A: Multiplication is a fundamental mathematical operation crucial for problem-solving in various fields, from everyday finances to advanced scientific calculations. It forms the base for understanding more complex mathematical concepts.
-
Q: Are there other ways to solve this problem besides the ones mentioned?
- A: While the methods discussed are common and effective, other approaches exist, such as using a calculator or specialized multiplication methods. The most efficient method depends on the context and individual preferences.
-
Q: How can I improve my multiplication skills?
- A: Practice is key! Regularly solving multiplication problems, using different methods, and exploring real-world applications will significantly improve your skills and build your confidence. Utilizing online resources and interactive games can also be a fun and effective way to improve.
Conclusion: More Than Just a Number
The seemingly simple problem of 33 x 5 serves as a gateway to understanding the broader world of mathematics. By exploring different methods and applications, we've moved beyond simply finding the answer (165) to appreciating the underlying principles and the practical relevance of this basic arithmetic operation. Mastering multiplication is not just about memorizing facts; it's about developing a deeper understanding of numbers and their relationships, a skill that will serve you well throughout your life. The journey from understanding the basics to applying the knowledge in diverse scenarios is a testament to the power of mathematical concepts, even those as seemingly simple as 33 x 5. Remember, consistent practice and a curious mind are the keys to unlocking the full potential of mathematical understanding.
Latest Posts
Latest Posts
-
0 75 X 5
Sep 15, 2025
-
134lbs In Kg
Sep 15, 2025
-
96km In Miles
Sep 15, 2025
-
Feeding Past Tense
Sep 15, 2025
-
3ab 9ab 7ab
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 33 X 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.