3/4 Of 48
stanleys
Sep 15, 2025 · 5 min read
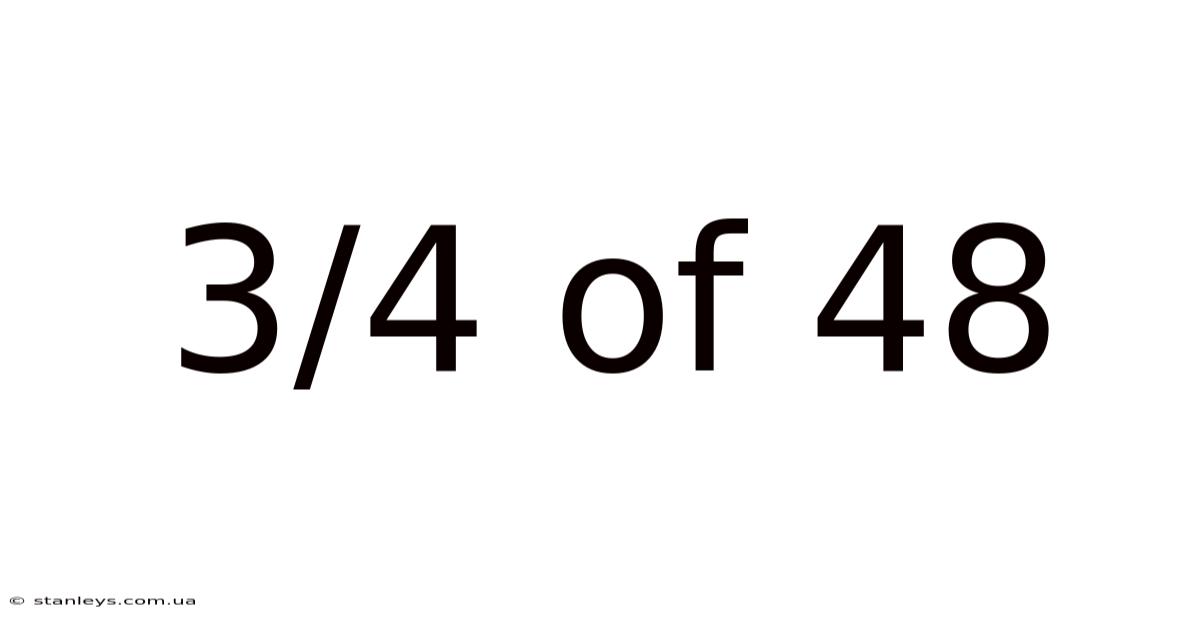
Table of Contents
Decoding 3/4 of 48: A Deep Dive into Fractions and Their Applications
Finding 3/4 of 48 might seem like a simple arithmetic problem, suitable only for elementary school students. However, understanding this seemingly basic calculation opens a door to a broader comprehension of fractions, their practical applications, and even their role in more advanced mathematical concepts. This article will not only solve the problem but also explore the underlying principles, different methods of solution, and real-world examples where understanding fractions like 3/4 is crucial. We will delve into the meaning of fractions, their representation, and how they relate to percentages and decimals, making this a comprehensive guide for anyone looking to solidify their understanding of this fundamental mathematical concept.
Understanding Fractions: A Building Block of Mathematics
Before we tackle 3/4 of 48, let's establish a strong foundation in fractions. A fraction represents a part of a whole. It is expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into. In the fraction 3/4, 3 is the numerator and 4 is the denominator. This means we are considering 3 out of 4 equal parts of a whole.
Method 1: Direct Calculation – Multiplication of Fractions
The most straightforward way to find 3/4 of 48 is to multiply the fraction 3/4 by the whole number 48. Remember that any whole number can be written as a fraction with a denominator of 1. Therefore, we can rewrite 48 as 48/1.
The calculation is as follows:
(3/4) * (48/1) = (3 * 48) / (4 * 1) = 144 / 4 = 36
Therefore, 3/4 of 48 is 36.
Method 2: Finding One-Fourth and Multiplying
Another approach involves finding one-fourth (1/4) of 48 first, and then multiplying the result by 3 to obtain three-fourths (3/4).
To find 1/4 of 48, we divide 48 by 4:
48 / 4 = 12
Now, multiply this result by 3 to find 3/4 of 48:
12 * 3 = 36
This method reinforces the understanding that a fraction represents a division. We find the value of one part (1/4) and then scale it up to find the required number of parts (3/4).
Method 3: Converting the Fraction to a Decimal
We can also convert the fraction 3/4 into its decimal equivalent before multiplying. To do this, we divide the numerator (3) by the denominator (4):
3 / 4 = 0.75
Now, multiply this decimal by 48:
0.75 * 48 = 36
This method highlights the interchangeability between fractions and decimals, showing that they represent the same proportional value.
Method 4: Visual Representation – Using a Diagram
A visual representation can be very helpful, especially for beginners. Imagine a rectangle divided into four equal parts. Each part represents 1/4. To find 3/4, we shade three of these parts. If the entire rectangle represents 48, then each part (1/4) represents 12 (48 / 4 = 12). Shading three parts gives us 12 * 3 = 36. This visual approach makes the concept of fractions more intuitive.
Real-World Applications of Fractions: Beyond the Classroom
The seemingly simple calculation of 3/4 of 48 has numerous practical applications in everyday life and various professions.
-
Cooking and Baking: Recipes often use fractions. For example, a recipe might call for 3/4 cup of flour. Understanding fractions is essential for accurate measurements and consistent results.
-
Construction and Engineering: Fractions are crucial in measuring materials and dimensions. Engineers and architects rely on precise fractional measurements to ensure the structural integrity and functionality of buildings and other structures.
-
Finance: Fractions are used extensively in finance, particularly when dealing with percentages, interest rates, and stock prices. Understanding fractions is critical for making informed financial decisions.
-
Data Analysis: In data analysis, fractions and percentages are frequently used to represent proportions and trends within datasets.
-
Retail and Sales: Discounts are often expressed as fractions (e.g., 1/4 off). Understanding fractions helps consumers calculate the final price after a discount.
-
Time Management: We use fractions when talking about time (e.g., 3/4 of an hour). This is crucial for scheduling and time management.
Expanding the Understanding: Percentages and Decimals
The fraction 3/4 is closely related to percentages and decimals. To convert a fraction to a percentage, we multiply it by 100%:
(3/4) * 100% = 75%
This means 3/4 is equivalent to 75%. We already saw how to convert the fraction to a decimal (0.75) earlier. The ability to convert between fractions, decimals, and percentages is crucial for various applications.
Frequently Asked Questions (FAQs)
Q: What if the number wasn't divisible by 4?
A: If the number wasn't easily divisible by 4, you could still use the multiplication method: (3/4) * (number). You might end up with a fraction as a result, which you could then simplify or convert to a decimal.
Q: Are there other ways to represent 3/4?
A: Yes, 3/4 can also be represented as 6/8, 9/12, 12/16, and so on. These are all equivalent fractions because they represent the same proportional value.
Q: Why is understanding fractions important?
A: Understanding fractions is fundamental to mathematics and has wide-ranging applications in various fields, from everyday life to complex scientific calculations. It builds a solid foundation for future mathematical learning.
Conclusion: Mastering Fractions for a Brighter Future
Finding 3/4 of 48, while seemingly simple, provides a valuable opportunity to explore the world of fractions in depth. From direct multiplication to visual representations, different approaches highlight the versatility of fractions and their interconnectedness with decimals and percentages. Mastering fractions is not just about solving arithmetic problems; it’s about developing a strong foundation for critical thinking, problem-solving, and a deeper understanding of the world around us. The applications of this fundamental mathematical concept are vast and permeate numerous aspects of our lives, reinforcing the importance of a solid grasp of fractional arithmetic. So, next time you encounter a fraction, remember the journey we took to understand 3/4 of 48 – a journey that opens up a world of mathematical possibilities.
Latest Posts
Latest Posts
-
5 Of 190
Sep 15, 2025
-
5 Of 1000000
Sep 15, 2025
-
Kinetic Energy Calculator
Sep 15, 2025
-
Half Of 55
Sep 15, 2025
-
Mmolar To Um
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 3/4 Of 48 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.