33 X 4
stanleys
Sep 15, 2025 · 5 min read
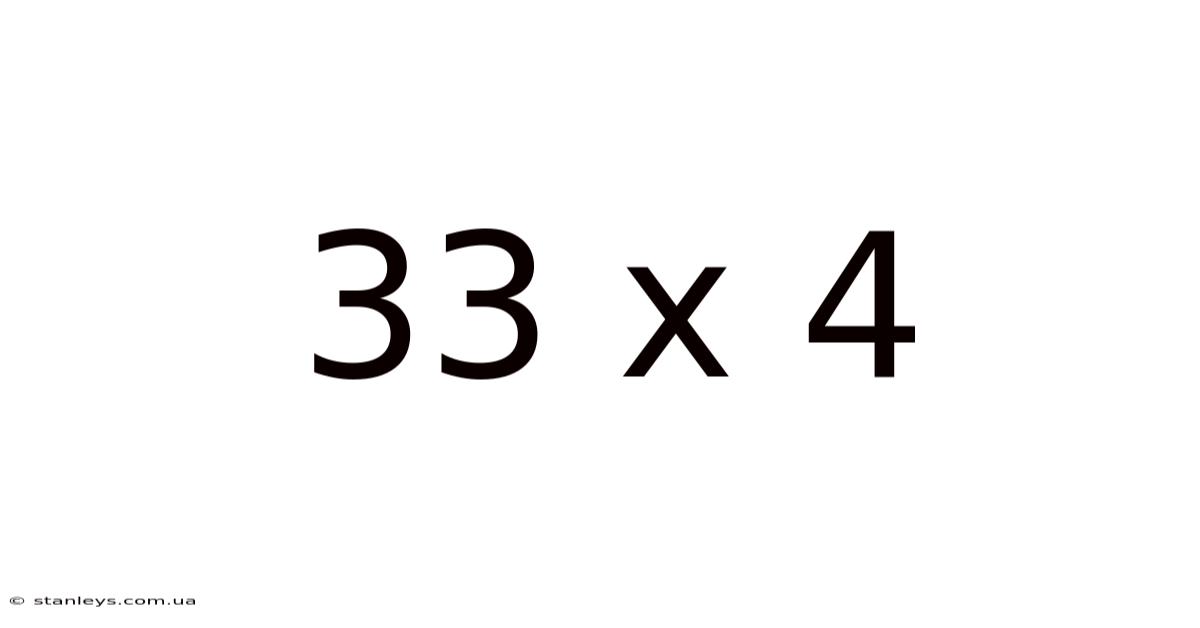
Table of Contents
Unlocking the Mystery of 33 x 4: A Deep Dive into Multiplication
This article explores the seemingly simple multiplication problem of 33 x 4, delving far beyond the immediate answer to uncover the underlying mathematical concepts and practical applications. We'll examine various methods for solving this problem, discuss the significance of multiplication in everyday life, and even touch upon its role in more advanced mathematical fields. Understanding 33 x 4 isn't just about getting the right answer; it's about grasping the fundamental building blocks of arithmetic and appreciating their widespread importance.
Introduction: More Than Just a Number
At first glance, 33 x 4 might appear trivial. It's a basic multiplication problem easily solvable by most elementary school students. However, this seemingly simple equation offers a gateway to understanding crucial mathematical concepts, from the distributive property to the relationship between multiplication and addition. This exploration will not only provide the solution to 33 x 4 but will also illuminate the broader context of multiplication within the world of mathematics and beyond. We will cover various methods of calculation, exploring both traditional and alternative approaches, ensuring a comprehensive understanding for readers of all levels.
Method 1: Traditional Multiplication
The most common method for solving 33 x 4 involves the standard multiplication algorithm taught in schools. This method involves multiplying each digit of 33 by 4, starting from the rightmost digit (the units place).
- Multiply the units digit: 4 x 3 = 12. Write down '2' and carry-over '1'.
- Multiply the tens digit: 4 x 3 = 12. Add the carry-over '1': 12 + 1 = 13. Write down '13'.
- Combine the results: The final answer is 132.
Therefore, 33 x 4 = 132.
Method 2: Distributive Property
The distributive property of multiplication over addition states that a(b + c) = ab + ac. We can apply this property to break down 33 x 4 into smaller, more manageable calculations:
33 x 4 = (30 + 3) x 4 = (30 x 4) + (3 x 4) = 120 + 12 = 132
This method highlights the relationship between multiplication and addition, showing how multiplication can be viewed as repeated addition. It's particularly useful for mental calculation and for understanding the underlying principles of multiplication.
Method 3: Repeated Addition
This is the most fundamental approach to multiplication. It simply involves adding 33 four times:
33 + 33 + 33 + 33 = 132
While this method is straightforward, it can become cumbersome with larger numbers. However, it serves as a valuable tool for visualizing multiplication and reinforcing its connection to addition.
Method 4: Lattice Multiplication
Lattice multiplication is a visual method that can be helpful for understanding the process of multiplying larger numbers. While it might seem more complex for 33 x 4, it illustrates a powerful technique applicable to more challenging multiplications.
(Here, a visual representation of lattice multiplication for 33 x 4 would be included if this were a visual document. The process involves drawing a grid, placing the digits of 33 along the top and 4 along the side, performing individual multiplications within the grid, and then summing the diagonals.)
The Significance of Multiplication: Real-World Applications
Multiplication is far from an abstract mathematical concept; it's a crucial tool used extensively in daily life. Consider these examples:
- Shopping: Calculating the total cost of multiple items at the same price (e.g., 4 packs of juice at $33 each).
- Cooking: Doubling or tripling a recipe requires multiplying the ingredient quantities.
- Construction: Determining the amount of materials needed for a project (e.g., calculating the number of bricks needed for a wall).
- Finance: Calculating interest, taxes, or discounts often involves multiplication.
- Travel: Determining the total distance traveled over multiple days or the cost of fuel for a journey.
These examples demonstrate the practical relevance of multiplication, highlighting its importance in various aspects of daily life. Understanding multiplication, even at a simple level like 33 x 4, equips individuals with essential problem-solving skills applicable across numerous contexts.
Multiplication in Advanced Mathematics
The concept of multiplication extends far beyond basic arithmetic. It plays a pivotal role in:
- Algebra: Solving algebraic equations often involves multiplying variables and constants.
- Calculus: Derivatives and integrals frequently involve multiplicative operations.
- Linear Algebra: Matrices are multiplied to represent transformations and solve systems of linear equations.
- Number Theory: Concepts like prime factorization and modular arithmetic rely heavily on multiplication.
Understanding multiplication at a fundamental level, as exemplified by the seemingly simple 33 x 4, provides a solid foundation for exploring these more advanced mathematical concepts.
Frequently Asked Questions (FAQ)
-
Q: What is the fastest way to solve 33 x 4? A: The fastest method depends on individual preference and mathematical aptitude. For this particular problem, mental math using the distributive property ((30 x 4) + (3 x 4)) is often quickest.
-
Q: Are there other ways to calculate 33 x 4 besides the methods mentioned? A: Yes, various alternative algorithms and techniques exist, but the methods discussed above represent the most common and readily accessible approaches.
-
Q: Why is understanding multiplication important? A: Multiplication is fundamental to many aspects of mathematics and is crucial for problem-solving in everyday life, from shopping to complex scientific calculations.
-
Q: Can I use a calculator to solve 33 x 4? A: While a calculator provides a quick solution, understanding the underlying methods is crucial for developing mathematical skills and appreciating the concept of multiplication.
Conclusion: The Enduring Power of 33 x 4
While the calculation of 33 x 4 might seem inconsequential, its significance extends far beyond a single numerical answer. It represents a fundamental building block of mathematics, illustrating the interconnectedness of addition and multiplication, and highlighting the practical applications of this essential arithmetic operation. By exploring various methods of solving this problem and understanding its broader implications, we gain a deeper appreciation for the power and versatility of mathematics in our daily lives and its crucial role in more advanced mathematical studies. The simplicity of 33 x 4 belies its profound implications within the vast and intricate world of numbers. The answer, 132, is merely the starting point of a much larger and more enriching mathematical journey.
Latest Posts
Latest Posts
-
0 75 X 5
Sep 15, 2025
-
134lbs In Kg
Sep 15, 2025
-
96km In Miles
Sep 15, 2025
-
Feeding Past Tense
Sep 15, 2025
-
3ab 9ab 7ab
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 33 X 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.