X 3 5
stanleys
Sep 15, 2025 · 6 min read
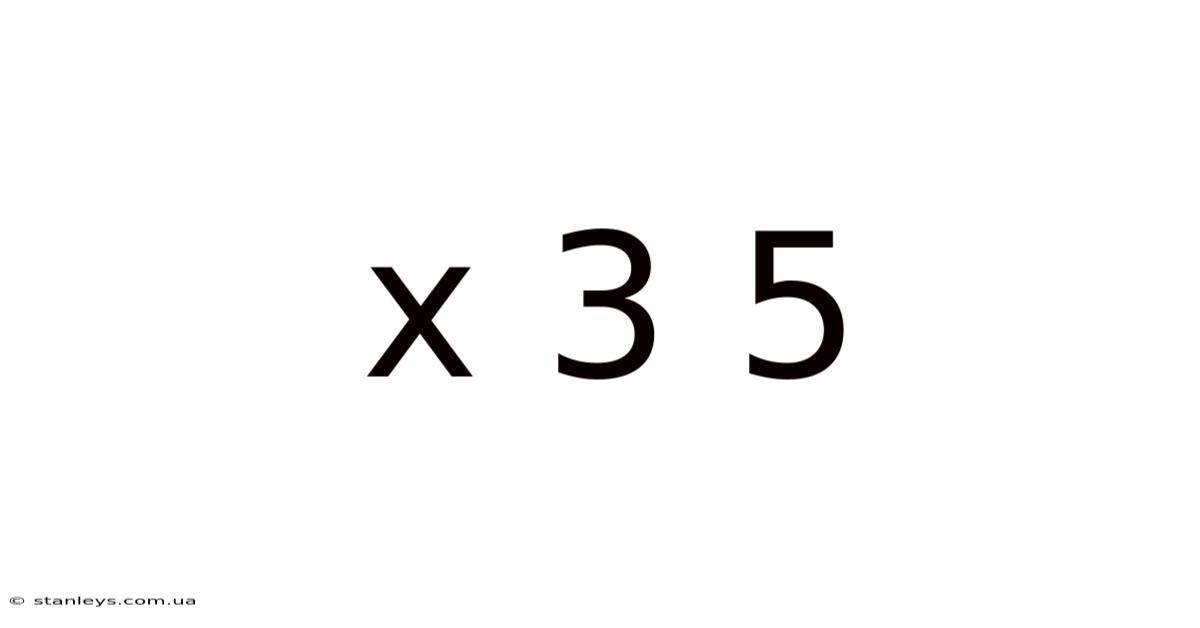
Table of Contents
Decoding x³ + 5: A Deep Dive into Cubic Equations and Beyond
This article explores the seemingly simple algebraic expression x³ + 5, delving into its mathematical properties, solving methods, and broader implications within the realm of algebra and beyond. We'll unpack the concept of cubic equations, explore various solution techniques, and touch upon the historical context and real-world applications of such equations. Understanding x³ + 5 is a gateway to appreciating the beauty and power of higher-order polynomial equations.
Understanding Cubic Equations
A cubic equation is a polynomial equation of degree three. The general form is expressed as ax³ + bx² + cx + d = 0, where a, b, c, and d are constants, and a ≠ 0. Our focus, x³ + 5, is a simplified version of this general form, where b = c = 0 and d = -5. This means we are dealing with a monic cubic equation (where the coefficient of x³ is 1) with no quadratic or linear terms. This simplification makes it a relatively easier case to solve compared to more complex cubic equations.
Solving x³ + 5 = 0
Solving x³ + 5 = 0 involves finding the values of x that satisfy the equation. Our primary goal is to isolate x. Let's break down the steps:
-
Isolate the x³ term: Subtract 5 from both sides of the equation: x³ = -5
-
Take the cube root: To solve for x, we need to take the cube root of both sides: x = ∛(-5)
This gives us one real root. However, it's crucial to remember that cubic equations always have three roots (considering complex numbers). While the cube root of a negative number yields a negative real number, the other two roots are complex conjugates.
Let's explore the concept of complex numbers further.
Complex Numbers and the Fundamental Theorem of Algebra
The expression ∛(-5) results in a real number, approximately -1.71. However, the Fundamental Theorem of Algebra states that a polynomial of degree n has exactly n roots (counting multiplicity) in the complex number system. This means our cubic equation, x³ + 5 = 0, has three roots. Since we've found one real root, the other two must be complex.
Complex numbers are numbers of the form a + bi, where 'a' and 'b' are real numbers, and 'i' is the imaginary unit (√-1). To find the complex roots, we need to use the polar form of complex numbers and De Moivre's Theorem.
Finding the Complex Roots using De Moivre's Theorem
De Moivre's Theorem provides a method for computing powers and roots of complex numbers. First, we express -5 in polar form:
- Magnitude (r): r = |-5| = 5
- Argument (θ): θ = π (since -5 lies on the negative real axis)
Now, we can express -5 in polar form as 5(cos(π) + i sin(π)). To find the cube roots, we use De Moivre's Theorem:
z<sup>1/n</sup> = r<sup>1/n</sup> [cos((θ + 2kπ)/n) + i sin((θ + 2kπ)/n)]
Where:
- z is the complex number (-5 in our case)
- n is the root (3 in our case - cube root)
- k is an integer (0, 1, 2 for the three roots)
Applying this to our equation:
- k = 0: x₁ = 5<sup>1/3</sup> [cos(π/3) + i sin(π/3)] ≈ 1.71 + 1.71i
- k = 1: x₂ = 5<sup>1/3</sup> [cos(π) + i sin(π)] ≈ -1.71
- k = 2: x₃ = 5<sup>1/3</sup> [cos(5π/3) + i sin(5π/3)] ≈ 1.71 - 1.71i
Therefore, the three roots of x³ + 5 = 0 are approximately -1.71, 1.71 + 1.71i, and 1.71 - 1.71i. Note that the two complex roots are complex conjugates, a common characteristic of polynomials with real coefficients.
Numerical Methods for Solving Cubic Equations
While the analytical approach using De Moivre's Theorem provides exact solutions, numerical methods are often necessary for more complex cubic equations. These methods approximate the roots through iterative processes. Some common numerical methods include:
- Newton-Raphson Method: This iterative method refines an initial guess for the root using the derivative of the function.
- Bisection Method: This method repeatedly halves an interval known to contain a root until the desired accuracy is achieved.
- Secant Method: Similar to the Newton-Raphson method, but it approximates the derivative using finite differences.
These methods are particularly useful when analytical solutions are difficult or impossible to obtain.
Historical Context of Cubic Equations
The history of solving cubic equations is rich and fascinating. Italian mathematicians in the 16th century, particularly Scipione del Ferro and Niccolò Tartaglia, made significant breakthroughs in developing methods for solving cubic equations. Gerolamo Cardano later published these methods, leading to widespread understanding and application. This period marks a pivotal moment in the development of algebra, extending our ability to solve polynomial equations beyond the quadratic case.
Applications of Cubic Equations
Cubic equations arise in various fields, including:
- Engineering: Designing structures, analyzing fluid flow, and solving problems in thermodynamics often involve cubic equations.
- Physics: Modeling oscillations, projectile motion, and certain wave phenomena can utilize cubic equations.
- Chemistry: In chemical kinetics and equilibrium calculations, cubic equations can be encountered.
- Economics: Certain economic models and optimization problems may involve cubic equations.
- Computer Graphics: Cubic curves and surfaces (like Bezier curves) are fundamental in computer-aided design and animation.
Further Exploration: Beyond x³ + 5
The exploration of x³ + 5 serves as a foundation for understanding more complex polynomial equations. Higher-order polynomials (quartic, quintic, and beyond) also have their own set of properties and solution techniques. While general solutions exist for quartic equations, it has been proven that there's no general algebraic solution for polynomial equations of degree five or higher (Abel-Ruffini theorem). This theorem highlights the limitations of algebraic techniques and underscores the importance of numerical methods for solving these higher-order equations.
Frequently Asked Questions (FAQ)
-
Q: Can x³ + 5 be factored easily? A: Not in the traditional sense using real numbers. However, it can be factored using complex numbers, as shown in the complex root solutions.
-
Q: What if the equation was x³ - 5 = 0? A: The process would be similar, but the real root would be positive (∛5), and the complex roots would have different arguments.
-
Q: Are there graphical methods to solve cubic equations? A: Yes. Graphing the function y = x³ + 5 and finding where it intersects the x-axis visually represents the real root. However, graphical methods don't directly reveal the complex roots.
-
Q: Are there online calculators or software to solve cubic equations? A: Yes, numerous online calculators and mathematical software packages (like Mathematica or MATLAB) can solve cubic (and higher-order) equations numerically or symbolically.
Conclusion
The seemingly simple equation x³ + 5 = 0 opens a window into the fascinating world of cubic equations and the broader landscape of algebra. By understanding the methods for finding its roots—both real and complex—we gain insights into the fundamental theorem of algebra, the power of complex numbers, and the diverse applications of these equations in various fields. From analytical solutions using De Moivre's theorem to numerical methods for more complex scenarios, the journey of solving x³ + 5 provides a solid foundation for further exploration into the intricacies of higher-order polynomial equations and their profound impact on mathematics and beyond. The seemingly straightforward equation holds a depth and complexity that warrants careful study and appreciation.
Latest Posts
Latest Posts
-
X 2 4x
Sep 15, 2025
-
0 07 In Fraction
Sep 15, 2025
-
Ashfields Polo Club
Sep 15, 2025
-
Opposite To Gentle
Sep 15, 2025
-
38 8f To C
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about X 3 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.