X 2 4x
stanleys
Sep 15, 2025 · 6 min read
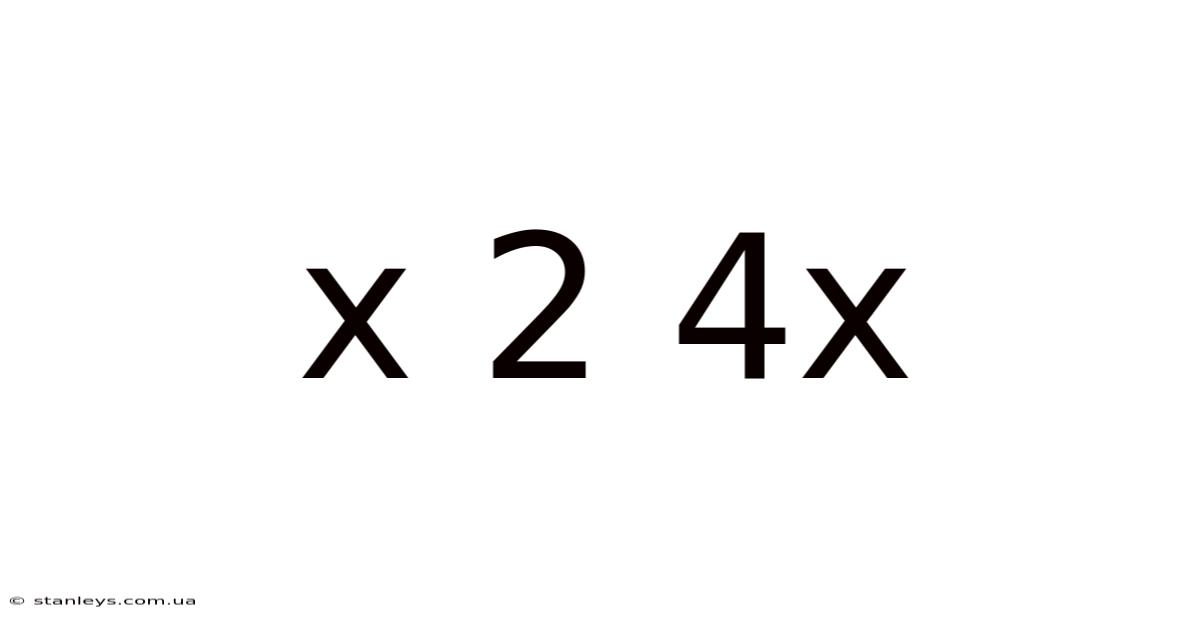
Table of Contents
Decoding the Mystery: A Deep Dive into x² + 4x
The expression x² + 4x is a fundamental concept in algebra, appearing frequently in various mathematical contexts. Understanding its properties, manipulations, and applications is crucial for anyone pursuing a path in mathematics, science, or engineering. This comprehensive guide will dissect this seemingly simple expression, unveiling its underlying structure, demonstrating various solution methods, and exploring its real-world applications. We'll go beyond the basic understanding to delve into its complexities and significance.
Introduction: Understanding the Quadratic Expression
The expression x² + 4x represents a quadratic expression. Quadratic expressions are characterized by the presence of a variable raised to the power of two (a squared term), along with a linear term (a variable raised to the power of one), and sometimes a constant term. In this case, we have a quadratic expression lacking a constant term. This seemingly simple omission significantly impacts its behavior and how we approach solving problems involving it.
1. Factoring the Expression
One of the most fundamental techniques in algebra is factoring. Factoring involves expressing a given expression as a product of simpler expressions. For x² + 4x, we can factor out a common factor, which is 'x'. This simplifies the expression to:
x(x + 4)
This factored form reveals a crucial aspect of the expression. The expression equals zero when either x = 0 or x = -4. These values are called the roots or zeros of the quadratic expression. Understanding the roots is essential for solving equations and analyzing the behavior of functions related to this expression.
2. Completing the Square: Unveiling the Vertex
Another powerful technique for manipulating quadratic expressions is completing the square. This method transforms the expression into a perfect square trinomial, plus a remaining constant. Completing the square allows us to determine the vertex of the parabola represented by the quadratic function y = x² + 4x. This is crucial for graphing and understanding the function's behavior.
The process involves manipulating the expression to fit the form (x + a)² + b, where 'a' and 'b' are constants. For x² + 4x:
- Identify the coefficient of the linear term: The coefficient of x is 4.
- Divide the coefficient by 2: 4 / 2 = 2
- Square the result: 2² = 4
- Add and subtract this value: x² + 4x + 4 - 4
- Rewrite as a perfect square: (x + 2)² - 4
Now, the expression is in the form (x + a)² + b, where a = 2 and b = -4. This reveals the vertex of the parabola at (-2, -4). The vertex represents the minimum point of the parabola since the coefficient of the x² term is positive.
3. Graphing the Quadratic Function y = x² + 4x
The quadratic function y = x² + 4x can be graphically represented as a parabola. Understanding its graph helps visualize the function's behavior and its relationship to the roots and the vertex. Key features of the graph include:
- Vertex: (-2, -4), determined through completing the square.
- x-intercepts: (0, 0) and (-4, 0), corresponding to the roots of the equation x² + 4x = 0.
- y-intercept: (0, 0), obtained by setting x = 0.
- Axis of symmetry: x = -2, a vertical line passing through the vertex.
- Concavity: The parabola opens upwards since the coefficient of x² (which is 1) is positive.
Plotting these points and sketching the curve creates a visual representation of the quadratic function, offering a clear understanding of its behavior across different values of x.
4. Solving Quadratic Equations: Finding the Roots
The expression x² + 4x becomes a quadratic equation when set equal to a constant. For example, consider the equation x² + 4x = 0. There are several methods to solve such equations:
- Factoring: As shown previously, factoring x² + 4x to x(x + 4) = 0 readily yields the roots x = 0 and x = -4.
- Quadratic Formula: For more complex quadratic equations, the quadratic formula provides a general solution:
x = [-b ± √(b² - 4ac)] / 2a
where a, b, and c are the coefficients of the quadratic equation ax² + bx + c = 0. In our case (x² + 4x = 0), a = 1, b = 4, and c = 0. Applying the formula gives the same roots: x = 0 and x = -4.
- Completing the Square: This method can also be used to solve quadratic equations. By completing the square, we transform the equation into a solvable form. For example, solving x² + 4x = 5 using completing the square will give us x = 1 or x = -5.
5. Applications of x² + 4x in Real-World Scenarios
The seemingly simple expression x² + 4x finds surprisingly broad applications across various fields:
- Physics: Quadratic equations are frequently encountered in projectile motion calculations, where the height of a projectile over time can be modeled using a quadratic function. The expression could represent a component of such a function.
- Engineering: In structural engineering, quadratic equations can be used to model stress and strain on beams and other structures.
- Economics: Quadratic functions are used in optimization problems, such as maximizing profit or minimizing cost. The expression could be a part of a larger model representing revenue or cost functions.
- Computer Graphics: Quadratic curves are fundamental to creating smooth curves in computer graphics and animations.
6. Exploring Variations and Extensions
While we've focused on x² + 4x, understanding this expression lays a solid foundation for tackling more complex quadratic expressions and equations. Consider these variations:
- Adding a constant term: x² + 4x + c, where 'c' is a constant, introduces a y-intercept and shifts the parabola vertically.
- Changing the coefficient of x²: ax² + 4x, where 'a' is a constant, alters the parabola's width and concavity. A negative 'a' will cause the parabola to open downwards.
- Adding higher-order terms: Including terms with x raised to powers greater than 2 transforms the expression into a polynomial of higher degree, resulting in more complex behavior.
7. Frequently Asked Questions (FAQ)
-
Q: What is the difference between an expression and an equation?
- A: An expression is a mathematical phrase that combines numbers, variables, and operators. An equation is a statement that asserts the equality of two expressions.
-
Q: What are the roots of a quadratic equation?
- A: The roots, or zeros, are the values of x that make the quadratic equation equal to zero. These correspond to the x-intercepts on the graph of the quadratic function.
-
Q: Why is completing the square useful?
- A: Completing the square helps to find the vertex of a parabola and allows us to rewrite the quadratic expression in a form that is easier to solve or analyze.
-
Q: Can a quadratic equation have more than two roots?
- A: No, a quadratic equation can have at most two real roots. It might have one repeated root (a single x-intercept) or two distinct real roots (two x-intercepts).
-
Q: How do I choose the best method for solving a quadratic equation?
- A: Factoring is the easiest if the quadratic expression factors easily. The quadratic formula works for all quadratic equations, while completing the square can be useful for specific purposes, such as finding the vertex.
8. Conclusion: Mastering the Fundamentals
Understanding the expression x² + 4x, its properties, and its manipulations is a cornerstone of algebraic proficiency. From factoring and completing the square to graphing and solving quadratic equations, each technique provides a valuable tool for tackling more advanced mathematical concepts. The applications of this seemingly simple expression extend far beyond the classroom, demonstrating its importance in various fields. By mastering the fundamentals, you unlock the ability to analyze and solve a wide array of problems, strengthening your mathematical foundation and opening doors to numerous opportunities. The journey from understanding a basic algebraic expression to appreciating its profound applications is a testament to the power of mathematical exploration.
Latest Posts
Latest Posts
-
0 07 To Fraction
Sep 16, 2025
-
75 Of 44
Sep 16, 2025
-
2x 7 13
Sep 16, 2025
-
180 X 12
Sep 16, 2025
-
70000 12
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about X 2 4x . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.