0.07 To Fraction
stanleys
Sep 16, 2025 · 5 min read
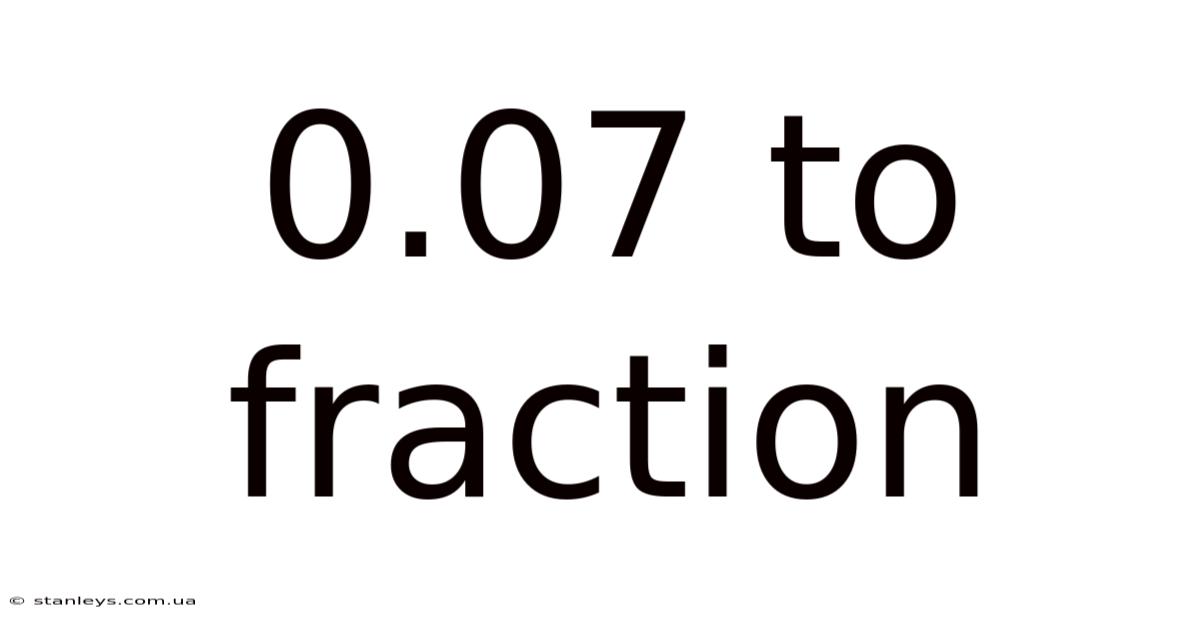
Table of Contents
Converting 0.07 to a Fraction: A Comprehensive Guide
Decimals and fractions are two fundamental ways to represent parts of a whole number. Understanding how to convert between them is a crucial skill in mathematics, applicable across various fields from basic arithmetic to advanced calculus. This comprehensive guide will walk you through the process of converting the decimal 0.07 into its fractional equivalent, explaining the steps clearly and providing additional insights into working with decimals and fractions. We'll explore different methods, address common misconceptions, and even tackle some related problems.
Understanding Decimals and Fractions
Before we delve into the conversion, let's refresh our understanding of decimals and fractions. A decimal represents a part of a whole using a base-ten system, where each digit to the right of the decimal point represents a power of ten. For instance, 0.07 means 7 hundredths (7/100).
A fraction, on the other hand, expresses a part of a whole as a ratio of two integers – a numerator (the top number) and a denominator (the bottom number). The denominator indicates the total number of parts the whole is divided into, while the numerator specifies how many of those parts are being considered.
Method 1: Direct Conversion using Place Value
The simplest method for converting 0.07 to a fraction leverages its place value. The digit 7 is in the hundredths place. Therefore, 0.07 can be directly written as the fraction 7/100. This fraction is already in its simplest form because 7 and 100 share no common factors other than 1.
Method 2: Using the Definition of a Decimal
A decimal number can be defined as a fraction with a denominator that is a power of 10. In this case:
0.07 = 7/100
This method reinforces the understanding that the number of decimal places corresponds to the power of 10 in the denominator. One decimal place means a denominator of 10, two decimal places mean a denominator of 100, three decimal places mean a denominator of 1000, and so on.
Method 3: Expanding the Decimal and Simplifying
While less efficient for simple decimals like 0.07, this method is valuable for understanding the underlying principles and is more versatile for more complex decimals.
We can rewrite 0.07 as:
0.07 = 0 + 0.07
This may seem trivial, but it sets the stage for writing 0.07 as a sum of fractions:
0.07 = 0/10 + 7/100 = 7/100
Here, we've expressed the decimal as a sum of fractions, each representing its place value. The result, 7/100, is already in its simplest form.
Simplifying Fractions: A Crucial Step
Although the direct conversion of 0.07 to 7/100 is straightforward, it's crucial to understand how to simplify fractions. Simplifying a fraction means reducing it to its lowest terms by dividing both the numerator and the denominator by their greatest common divisor (GCD). In the case of 7/100, the GCD of 7 and 100 is 1, meaning the fraction is already in its simplest form.
However, let's consider an example where simplification is necessary. Suppose we had the decimal 0.15.
-
Convert to a fraction: 15/100
-
Find the GCD of 15 and 100: The GCD is 5.
-
Divide both numerator and denominator by the GCD: (15/5) / (100/5) = 3/20
Therefore, 0.15 simplifies to 3/20. This step is essential for representing fractions in their most concise and manageable form.
Working with More Complex Decimals
The methods discussed above apply to more complex decimal numbers as well. Let's consider converting 0.375 to a fraction:
-
Write as a fraction: 375/1000
-
Find the GCD: The GCD of 375 and 1000 is 125.
-
Simplify: (375/125) / (1000/125) = 3/8
Therefore, 0.375 is equivalent to 3/8. This demonstrates the versatility of the approach. Even with more complex decimals, the process remains consistent: convert to a fraction with a power of 10 as the denominator, then simplify by dividing both numerator and denominator by their GCD.
Recurring Decimals and Fractions
Recurring decimals, such as 0.333..., present a slightly different challenge. These cannot be directly converted using the place value method. Instead, you'll need to use algebraic techniques. For instance, to convert 0.333... to a fraction:
Let x = 0.333...
Multiply both sides by 10: 10x = 3.333...
Subtract the first equation from the second: 10x - x = 3.333... - 0.333...
This simplifies to 9x = 3, so x = 3/9, which simplifies further to 1/3.
This shows that recurring decimals require a more advanced approach involving algebraic manipulation to obtain their fractional representation.
Frequently Asked Questions (FAQ)
-
Q: Can all decimals be converted to fractions? A: Yes, all terminating decimals (decimals that end) can be expressed as fractions. Recurring decimals can also be expressed as fractions, but require a different method.
-
Q: What if the GCD is 1? A: If the GCD of the numerator and denominator is 1, the fraction is already in its simplest form and no further simplification is needed.
-
Q: Are there any online tools to help with conversions? A: While this article encourages understanding the process, many online calculators can perform decimal-to-fraction conversions. However, it is important to understand the underlying principles for a complete grasp of the concept.
-
Q: Why is it important to learn decimal-to-fraction conversions? A: This skill is fundamental in mathematics and has applications in various fields like science, engineering, and finance. Understanding both representations of numbers enhances problem-solving capabilities.
Conclusion
Converting 0.07 to a fraction is a simple yet fundamental exercise in understanding the relationship between decimals and fractions. By understanding the place value of decimals, applying the principles of simplification, and recognizing the different approaches for various decimal types, you can confidently handle similar conversions. This skill is not just about rote memorization; it builds a strong foundation for more complex mathematical concepts. Remember that the key is to grasp the underlying principles – the method itself is straightforward, but the comprehension of the underlying mathematical concepts is what truly matters. Practice regularly, explore different types of decimal numbers, and soon you'll be comfortable converting decimals to fractions and vice-versa with ease and confidence.
Latest Posts
Related Post
Thank you for visiting our website which covers about 0.07 To Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.