Half Of 6
stanleys
Sep 13, 2025 · 5 min read
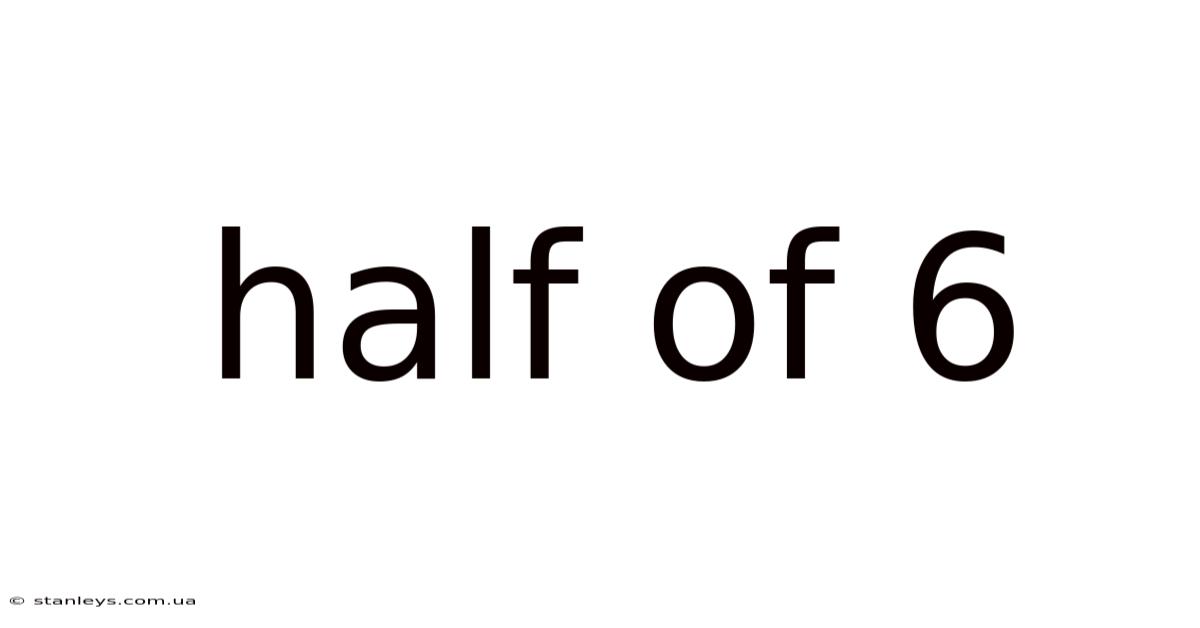
Table of Contents
Half of 6: A Deep Dive into Simple Arithmetic and its Broader Implications
What is half of 6? This seemingly simple question, suitable for even the youngest learners, actually opens a door to a fascinating exploration of fundamental mathematical concepts, their practical applications, and even their philosophical implications. This article will delve into the answer, exploring various approaches to solving the problem, examining the underlying principles, and considering the broader significance of this basic arithmetic operation in everyday life and beyond.
Understanding the Concept of "Half"
Before we tackle the specific problem of finding half of 6, let's clarify the concept of "half." Half refers to one of two equal parts of a whole. It's represented by the fraction ½, which means 1 divided by 2. Understanding this fundamental concept is crucial for grasping operations like halving and dividing by two. It's the cornerstone of many more complex mathematical concepts, and its intuitive understanding forms the basis for many real-world applications.
Calculating Half of 6: Different Methods
There are several ways to calculate half of 6, each illustrating different mathematical principles:
-
Division: The most straightforward method is simply dividing 6 by 2. 6 ÷ 2 = 3. This method emphasizes the core concept of splitting a whole into equal parts.
-
Fractions: We can express the problem as a fraction multiplication: ½ x 6 = 3. This method highlights the relationship between fractions and division, demonstrating that multiplying by ½ is equivalent to dividing by 2.
-
Visual Representation: Imagine six objects, such as apples or blocks. Dividing them equally into two groups will result in three objects in each group, visually demonstrating that half of 6 is 3. This method is particularly useful for younger learners or those who benefit from visual aids. It directly connects the abstract concept of "half" to a concrete, tangible example.
-
Repeated Subtraction: You can repeatedly subtract 2 from 6 until you reach 0. The number of times you subtract 2 is the answer. 6 - 2 = 4; 4 - 2 = 2; 2 - 2 = 0. This took three subtractions, showing that half of 6 is 3. This method introduces a different approach to division and emphasizes the iterative nature of some mathematical processes.
All these methods lead to the same answer: half of 6 is 3.
The Importance of Halving in Everyday Life
The seemingly trivial calculation of half of 6 has widespread applications in everyday life. Consider these examples:
-
Sharing: Dividing resources equally among two people is a common scenario. If you have 6 cookies and want to share them equally with a friend, you would give each person 3 cookies – half of the total.
-
Measurement: Halving is frequently used in measurement and cooking. If a recipe calls for 6 cups of flour and you want to halve the recipe, you would use 3 cups.
-
Money: Calculating discounts often involves halving. A "50% off" sale means paying half the original price. If an item costs $6, a 50% discount would reduce the price to $3.
-
Geometry: Halving plays a significant role in geometry. Finding the midpoint of a line segment, bisecting an angle, or dividing a shape into equal halves all rely on the concept of halving.
Expanding the Concept: Beyond Whole Numbers
The concept of "half" extends beyond whole numbers. We can find half of any number, including decimals and fractions:
-
Half of a decimal: Half of 6.5 is 6.5 ÷ 2 = 3.25
-
Half of a fraction: Half of 6/4 is (6/4) ÷ 2 = 6/8 = ¾
This demonstrates the versatility and adaptability of the halving operation across different number systems.
Halving in More Advanced Mathematics
While finding half of 6 seems elementary, the concept of halving and division by two has profound implications in more advanced mathematical fields:
-
Calculus: Differentiation and integration, fundamental concepts in calculus, often involve halving or dividing by two in various formulas and theorems.
-
Algebra: Solving equations often requires manipulating expressions that involve division by two or halving quantities.
-
Probability and Statistics: Calculating probabilities often involves dividing by two or using fractions that are related to halving.
-
Computer Science: Binary code, the foundation of computer programming, is based on the binary system, which uses only two digits (0 and 1). Many computer operations inherently involve halving or dividing by powers of two.
Exploring the Philosophical Implications
The act of halving, seemingly simple, can prompt philosophical reflection:
-
Balance and Symmetry: Halving represents a fundamental aspect of balance and symmetry, concepts that are important in art, design, and nature. The division of a whole into two equal parts creates a sense of equilibrium and harmony.
-
Division and Unity: The concept of halving explores the relationship between division and unity. While we divide a whole into parts, those parts remain intrinsically linked to the original whole.
-
The Nature of Reality: Some philosophical schools of thought explore the concept of duality and the division of reality into opposing forces. The act of halving can be seen as a metaphor for this fundamental duality.
Frequently Asked Questions (FAQs)
-
What is the opposite of halving? Doubling (or multiplying by 2) is the opposite of halving.
-
Can you halve a negative number? Yes, halving a negative number results in a smaller negative number. For example, half of -6 is -3.
-
How do you halve a fraction? You halve a fraction by multiplying the denominator by 2. For example, half of ¾ is 3/8. Alternatively, you can multiply the fraction by ½.
-
Why is halving important in programming? Binary operations, crucial in computer science, rely on powers of two, and halving is fundamental to understanding these operations.
Conclusion: The Enduring Significance of a Simple Operation
Finding half of 6, while seemingly a basic arithmetic problem, reveals a wealth of mathematical concepts and practical applications. From everyday tasks like sharing resources to advanced calculations in fields like calculus, the principle of halving plays a significant role. Furthermore, its philosophical implications highlight the deeper connections between mathematics, symmetry, and our understanding of the world around us. The simplicity of the problem belies its profound significance, underscoring the power of fundamental mathematical principles and their enduring relevance across various disciplines and aspects of life. This exploration of a simple calculation ultimately reinforces the importance of understanding fundamental mathematical concepts, as they form the building blocks for more complex and sophisticated mathematical explorations. The journey from understanding half of 6 to grasping its broader implications demonstrates the inherent beauty and interconnectedness within the world of mathematics.
Latest Posts
Latest Posts
-
86f In C
Sep 13, 2025
-
5 6 15
Sep 13, 2025
-
Ron Weasley Rat
Sep 13, 2025
-
9 X Pi
Sep 13, 2025
-
37cm In Inches
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Half Of 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.