9 X Pi
stanleys
Sep 13, 2025 · 7 min read
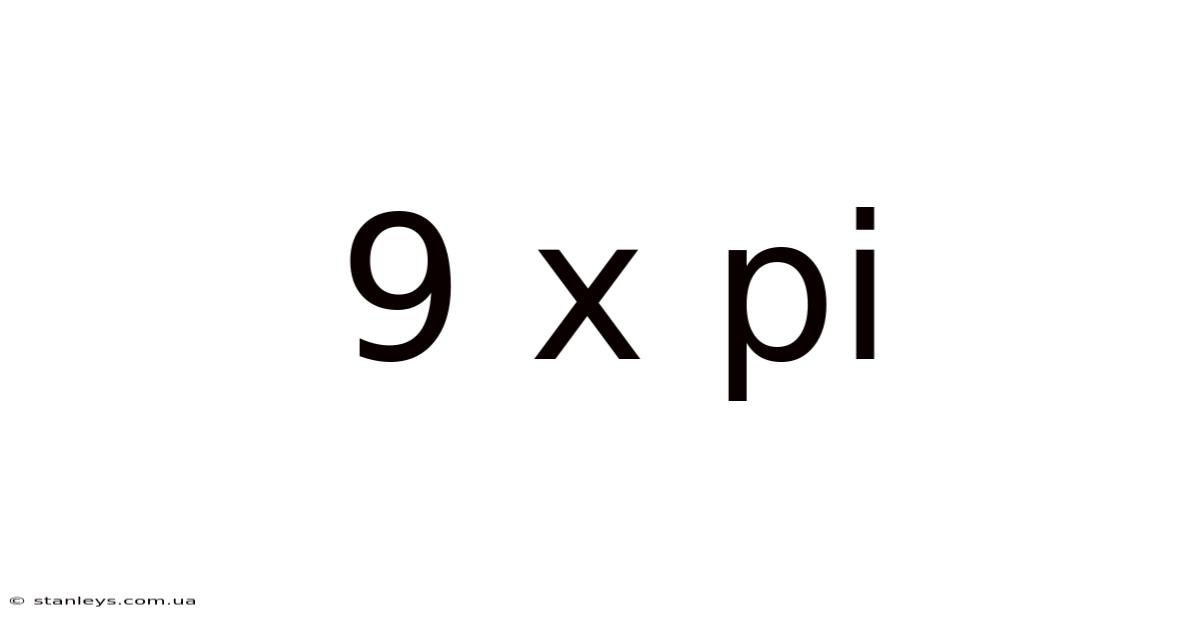
Table of Contents
Unveiling the Mysteries of 9π: A Deep Dive into Mathematics and its Applications
This article delves into the mathematical constant 9π (9 times pi), exploring its properties, calculations, and surprising applications across various fields. We'll move beyond a simple numerical value to understand the significance of this seemingly straightforward combination of a whole number and an irrational number. Understanding 9π requires a grasp of the fundamental concepts surrounding π itself, its approximations, and the practical uses of its multiples. Prepare for a fascinating journey into the heart of mathematics!
Understanding Pi (π)
Before we explore 9π, it's crucial to have a solid foundation in understanding π itself. π, or pi, is a mathematical constant representing the ratio of a circle's circumference to its diameter. It's approximately equal to 3.14159, but its decimal representation continues infinitely without repeating – it's an irrational number. This seemingly simple ratio underpins countless calculations in geometry, trigonometry, calculus, and beyond. Its presence in seemingly unrelated areas of mathematics highlights its fundamental importance. Understanding pi's irrationality is key to appreciating the complexity (and beauty) inherent in multiples like 9π.
Calculating 9π: Precision and Approximation
Calculating 9π is straightforward in principle: simply multiply 9 by the value of π. However, the precision of the result depends on the precision of the π value used. Using a calculator, a common approximation of 9π is 28.2743338823. This is accurate to several decimal places, sufficient for many practical applications. However, for applications requiring extremely high precision, such as advanced physics or engineering simulations, more digits of π are necessary.
The accuracy of 9π calculations depends directly on the accuracy of the π approximation employed. Historically, mathematicians have dedicated immense effort to calculating π to increasingly higher precision, using various sophisticated algorithms. These calculations are not merely academic exercises; the accuracy of these computations impacts the precision of real-world applications across multiple disciplines. The more precise the value of π used, the more precise the result for 9π will be. Modern computational power allows us to calculate π to trillions of digits, making the approximation of 9π virtually indistinguishable from its "true" value for most practical purposes.
The Significance of Multiples of Pi
The concept of multiplying π by integers, like in the case of 9π, is significant because it allows us to express and work with lengths, areas, and volumes related to circles, spheres, and other geometric figures in a precise manner. For example, the circumference of a circle with a radius of r is given by 2πr. Multiplying this by 9 would give us 18πr, representing the total length of 9 circumferences of such a circle.
Similarly, the area of a circle with radius r is given by πr². Consider a situation where we need to calculate the area of 9 such circles; the total area would then be 9πr². These straightforward examples demonstrate how multiples of π, including 9π, directly translate into geometrical calculations and estimations relevant to diverse scenarios in engineering, architecture, and other related fields. This seemingly simple multiplication hides a considerable practical power.
Applications of 9π in Various Fields
While 9π might not be as prominently featured as π itself, its applications are numerous and often indirect. Its presence manifests within broader calculations involving circles, spheres, and related geometrical figures.
-
Engineering: In civil engineering, calculations involving curved structures (like arches or domes) will often incorporate multiples of π. 9π could be a component of a larger calculation determining material requirements or structural stability. Similarly, mechanical engineering applications involving rotating components or calculations of cylindrical volumes would inevitably involve multiples of π, with 9π potentially appearing as a component within more complex equations.
-
Physics: In physics, particularly in fields like mechanics and electromagnetism, the presence of circular or spherical symmetries leads to the frequent appearance of π and its multiples. For instance, calculations involving gravitational fields around spherical objects or the behavior of electromagnetic waves in circular waveguides could incorporate 9π into the governing equations. The applications here are often subtle, embedded within more extensive calculations.
-
Computer Graphics and Game Development: In the digital realm, generating and manipulating circles and spheres is crucial for graphics rendering and game development. Rendering algorithms often involve repetitive calculations based on circles and spheres, resulting in the appearance of multiples of π like 9π within the complex code governing these graphical processes. While not directly visible, the number is crucial for correct representation of curved geometries.
-
Astronomy: Astronomical calculations often rely on geometrical models of celestial bodies, including spheres and circular orbits. Calculations related to orbits, planetary rotation, or the geometry of star systems will likely use π and its multiples extensively, indirectly incorporating 9π as a component of larger computations.
-
Mathematics Itself: Beyond its direct applications in other fields, 9π serves a role in pure mathematical investigations. It can appear within more advanced mathematical concepts such as integrals, series expansions, and Fourier transforms, particularly in problems with circular or spherical symmetries.
9π and its Relationship to Other Mathematical Constants
While 9π might seem isolated, it's intrinsically linked to other mathematical constants and functions. Its relationship with π is fundamental, as is its connection to other trigonometric functions and transcendental numbers. The fact that π itself is transcendental – meaning it's not the root of any non-zero polynomial with rational coefficients – adds another layer of complexity to understanding its multiples. The properties of π directly influence the properties of 9π, making its study a valuable avenue to explore deeper mathematical concepts.
Approximations and Error Analysis
Understanding the approximations inherent in working with 9π (due to the irrational nature of π) is vital. Error analysis is crucial to assess the reliability of calculations involving this constant. Using a truncated value of π inevitably introduces an error, and this error propagates through any calculations involving 9π. The magnitude of this error must be considered within the context of the application. For example, a minor error in calculating the volume of a sphere for a scientific experiment might be acceptable, but the same level of error could be catastrophic in designing a critical structural component.
Frequently Asked Questions (FAQ)
Q: Is 9π a rational or irrational number?
A: 9π is an irrational number. Since π is irrational (its decimal representation is infinite and non-repeating), any non-zero rational multiple of π (like 9π) will also be irrational.
Q: What is the exact value of 9π?
A: There is no exact decimal representation for 9π because π itself is irrational. We can only obtain increasingly precise approximations using more digits of π.
Q: What are the practical limitations of using an approximation of 9π?
A: Using an approximation introduces an error. The magnitude of this error depends on the precision of the π approximation used and the sensitivity of the application. For some applications, a rough approximation is sufficient; for others, high precision is essential.
Q: How is 9π used in computer programming?
A: In computer programming, 9π is usually represented using a high-precision floating-point approximation of π, multiplied by 9. The precision of this approximation depends on the programming language and the specific application. It might be crucial for tasks requiring accurate graphical representations of curved geometries or advanced physical simulations.
Q: Are there any special properties associated with 9π that distinguish it from other multiples of π?
A: No particular special mathematical properties uniquely distinguish 9π from other multiples of π. Its significance comes from its role within broader calculations involving circular and spherical geometries. The fact that it's a multiple of π is what makes it relevant in many applications.
Conclusion: The Enduring Relevance of 9π
In conclusion, while seemingly simple, 9π holds significant mathematical importance and wide-ranging practical applications. Its understanding necessitates a grasp of π's irrationality and the implications of using approximations. From engineering designs to complex scientific simulations and even the digital world of computer graphics, this seemingly basic combination of a whole number and a transcendental constant plays a surprisingly pivotal role in numerous calculations and processes. Its unassuming nature belies its profound influence across diverse fields, showcasing the beauty and interconnectedness of mathematics. The seemingly simple act of multiplying 9 and π opens a window into the intricacies of the mathematical world and its real-world impact.
Latest Posts
Latest Posts
-
24 30 Percentage
Sep 13, 2025
-
23 X 5
Sep 13, 2025
-
20 Of 125
Sep 13, 2025
-
38 5celsius To Fahrenheit
Sep 13, 2025
-
143 Pounds Kg
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 9 X Pi . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.