5 6 15
stanleys
Sep 13, 2025 · 7 min read
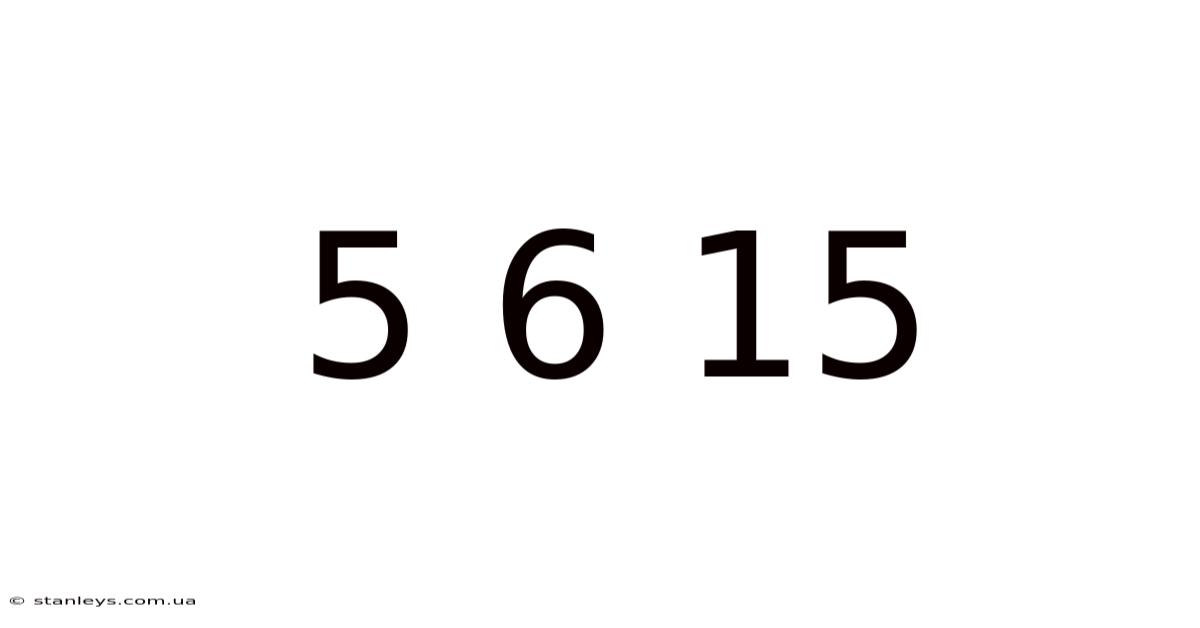
Table of Contents
Unlocking the Mysteries of 5, 6, and 15: A Deep Dive into Number Theory, Combinatorics, and More
The seemingly simple numbers 5, 6, and 15 hold a wealth of mathematical intrigue. This article explores their properties within various branches of mathematics, from basic arithmetic to more advanced concepts like number theory and combinatorics. We'll delve into their divisibility, prime factorization, relationships within number sequences, and their applications in various mathematical fields. Understanding these seemingly simple numbers reveals a fascinating glimpse into the intricate world of mathematics.
I. Introduction: The Foundation of Numbers
Before delving into the specifics of 5, 6, and 15, it's crucial to establish a foundational understanding of fundamental mathematical concepts. These numbers, like all integers, possess inherent properties that govern their behavior in mathematical operations. We'll examine their classifications (prime, composite, etc.), their prime factorizations, and their divisibility rules.
- Prime Numbers: A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. 5 is a prime number.
- Composite Numbers: A composite number is a positive integer that has at least one divisor other than 1 and itself. 6 and 15 are composite numbers.
- Prime Factorization: Every composite number can be expressed as a unique product of prime numbers. This factorization is crucial for various mathematical operations. The prime factorization of 6 is 2 x 3, and the prime factorization of 15 is 3 x 5.
- Divisibility Rules: Understanding divisibility rules helps determine if a number is divisible by another without performing long division. For instance, a number is divisible by 5 if its last digit is 0 or 5; a number is divisible by 6 if it's divisible by both 2 and 3; and a number is divisible by 15 if it's divisible by both 3 and 5.
II. Exploring the Individual Properties: 5, 6, and 15
Let's now examine the unique properties of each number individually:
A. The Number 5: A Prime with Unique Characteristics
5 is a prime number, meaning it's only divisible by 1 and itself. This seemingly simple fact has profound implications in number theory. Its presence in prime factorization significantly impacts the properties of composite numbers it's a part of. Furthermore, 5 plays a crucial role in various mathematical patterns and sequences. For instance, it features prominently in Fibonacci-like sequences and in modular arithmetic. The powers of 5 (5, 25, 125, 625, etc.) exhibit a specific pattern in their last digits, which is a subject of interest in number theory.
B. The Number 6: A Perfect Number's Precursor
6 is a composite number with a rich history in mathematics. It's the smallest perfect number, meaning it's equal to the sum of its proper divisors (1 + 2 + 3 = 6). This property has fascinated mathematicians for centuries and has led to research on other perfect numbers and their properties. The number 6 also appears in various geometric contexts; it's the number of sides in a hexagon, a common polygon in geometry. Its divisibility by both 2 and 3 makes it a significant number in modular arithmetic and number theory problems involving divisibility.
C. The Number 15: A Product of Primes
15 is a composite number whose prime factorization is 3 x 5. This simple factorization reveals its divisibility properties. It’s divisible by 1, 3, 5, and 15. Because it’s divisible by 3 and 5, it plays a role in problems involving multiples of 3 and 5. In combinatorics, it appears in problems involving permutations and combinations, particularly when dealing with choices from sets with 3 and 5 elements. Its appearance in various mathematical contexts highlights the importance of understanding prime factorization and its implications.
III. Relationships Between 5, 6, and 15: Exploring Connections
The three numbers, while distinct, are intertwined through several mathematical relationships.
- Divisibility: 15 is divisible by both 5 and 3, which are factors of 6. This interconnectedness demonstrates the hierarchical structure within the number system.
- Prime Factorization: The prime factorization of 15 (3 x 5) directly incorporates the prime number 5 and the factor 3, which is a factor in the prime factorization of 6 (2 x 3). This relationship showcases the fundamental role of prime numbers in understanding composite numbers.
- Modular Arithmetic: These numbers exhibit interesting patterns within modular arithmetic systems. For example, exploring their remainders when divided by different numbers (e.g., modulo 7, modulo 11) reveals cyclical patterns and properties applicable to cryptography and other fields.
IV. Applications in Advanced Mathematical Fields
The numbers 5, 6, and 15 appear in various advanced mathematical fields:
- Number Theory: These numbers serve as examples and test cases for various number-theoretic concepts like prime factorization, divisibility rules, modular arithmetic, and the distribution of prime numbers.
- Combinatorics: The number 15 frequently emerges in problems involving combinations and permutations, especially when dealing with selections from sets of 3 and 5 elements. For instance, calculating the number of ways to choose 3 items from a set of 5 employs the concept of combinations, where the number 15 could appear in the solution.
- Abstract Algebra: The properties of these numbers contribute to the study of groups, rings, and fields within abstract algebra. Their prime factorizations and divisibility properties are essential in constructing and analyzing algebraic structures.
- Geometry: The number 6 is fundamental in geometry, representing the number of sides in a hexagon and appearing in various geometric formulas and theorems. The number 5, while less directly involved in common geometric shapes, plays a role in more advanced geometrical concepts.
V. Practical Applications and Real-World Examples
While seemingly abstract, the properties of these numbers have practical applications:
- Cryptography: Modular arithmetic, where 5, 6, and 15 might play a role, is fundamental to modern encryption techniques.
- Computer Science: Understanding divisibility and prime factorization is crucial in algorithm design and optimization. The efficiency of certain algorithms depends heavily on the properties of the numbers involved, and 5, 6, and 15 can serve as illustrative examples.
- Coding Theory: Prime numbers and their properties are critical in error-correcting codes used in data transmission and storage. Numbers like 5 and the factors of 15 often appear in these applications.
VI. Frequently Asked Questions (FAQ)
Q1: Are 5, 6, and 15 related in any specific mathematical sequence?
A1: While they don't form a strictly defined sequence like the Fibonacci sequence, they are connected through their prime factorizations and divisibility properties. They appear in various mathematical sequences and patterns, often as elements within larger sets of numbers.
Q2: What's the significance of the perfect number 6 in relation to 5 and 15?
A2: The perfect number property of 6 highlights the unique characteristics of certain integers. The relationship to 5 and 15 lies primarily in the broader context of number theory. The fact that 6 is a perfect number is independent of the properties of 5 and 15 but sits alongside them within the field of number theory.
Q3: Can you provide a real-world example of the application of these numbers?
A3: Imagine a scenario where you need to distribute 15 items equally among groups. Knowing that 15 is divisible by 3 and 5 allows for efficient division into groups of 3 or 5. This simple example demonstrates how understanding divisibility plays a role in practical problem-solving.
VII. Conclusion: The Ongoing Fascination with Numbers
The seemingly simple numbers 5, 6, and 15 provide a gateway to understanding deeper mathematical concepts. Their exploration reveals the rich tapestry of number theory, combinatorics, and other mathematical fields. The interconnectedness of these numbers highlights the fundamental principles that govern the behavior of integers and their significance across various branches of mathematics. Furthermore, understanding their properties can lead to innovative solutions in fields such as computer science, cryptography, and coding theory. The journey into the world of numbers is a never-ending exploration, where seemingly simple concepts lead to profound insights. Continued exploration of numbers like 5, 6, and 15 helps to build a deeper appreciation for the beauty and elegance of mathematics.
Latest Posts
Latest Posts
-
24 30 Percentage
Sep 13, 2025
-
23 X 5
Sep 13, 2025
-
20 Of 125
Sep 13, 2025
-
38 5celsius To Fahrenheit
Sep 13, 2025
-
143 Pounds Kg
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 5 6 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.