20 Of 125
stanleys
Sep 13, 2025 · 6 min read
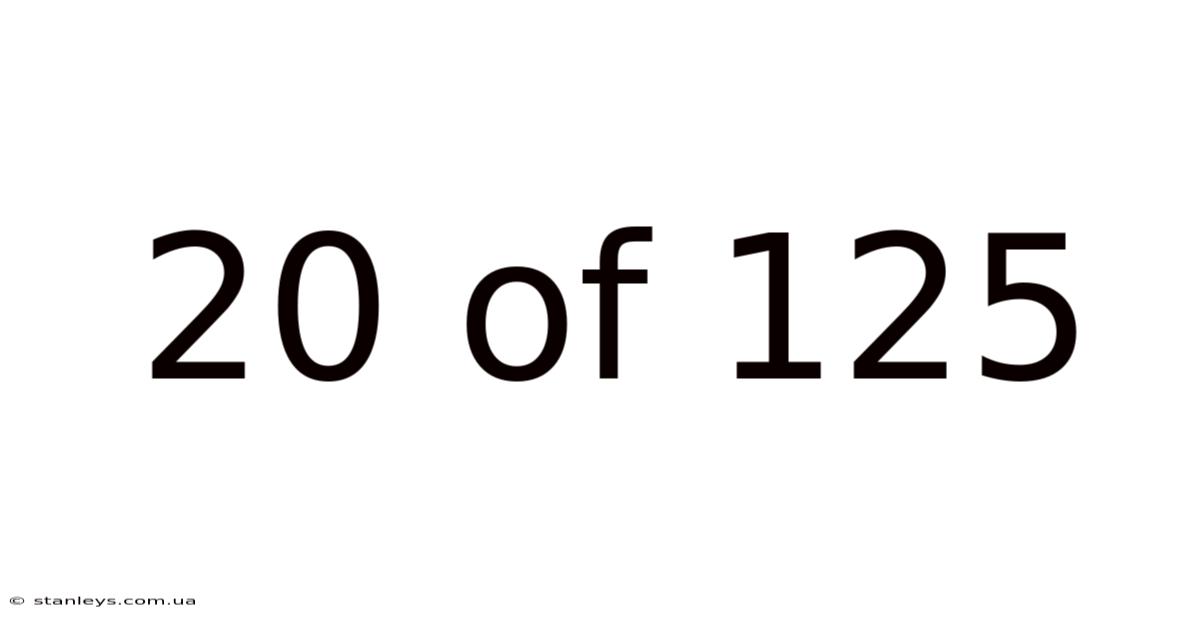
Table of Contents
Decoding the Mystery: 20 of 125 – A Deep Dive into Fractions, Ratios, and Proportions
Understanding fractions, ratios, and proportions is fundamental to success in mathematics and numerous real-world applications. This article delves into the meaning and significance of "20 of 125," exploring its representation as a fraction, ratio, and proportion, and highlighting its practical applications. We'll unravel the complexities behind this seemingly simple expression, making it accessible to learners of all levels. This comprehensive guide will equip you with the skills to confidently tackle similar problems and appreciate the interconnectedness of mathematical concepts.
Introduction: Understanding the Core Concepts
The expression "20 of 125" inherently represents a part-to-whole relationship. It signifies that 20 is a part of a larger whole, 125. This relationship can be expressed in various mathematical forms:
-
Fraction: A fraction represents a part of a whole. In this case, "20 of 125" is written as the fraction 20/125. The numerator (20) represents the part, and the denominator (125) represents the whole.
-
Ratio: A ratio compares two quantities. The ratio of 20 to 125 is written as 20:125 or 20/125. This signifies the relative sizes of the two quantities.
-
Proportion: A proportion is a statement that two ratios are equal. While "20 of 125" itself isn't a proportion, it can be used within a proportion to solve for an unknown quantity. For example, if we know that 20 out of 125 items are defective, we can set up a proportion to determine the number of defective items in a larger batch.
Simplifying the Fraction: Finding the Lowest Terms
The fraction 20/125 can be simplified by finding the greatest common divisor (GCD) of the numerator and denominator. The GCD of 20 and 125 is 5. Dividing both the numerator and the denominator by 5, we get:
20 ÷ 5 = 4 125 ÷ 5 = 25
Therefore, the simplified fraction is 4/25. This simplified form represents the same proportion but in its most concise representation. This simplification is crucial for easier calculations and understanding the relative size of the parts.
Decimal and Percentage Representation
To further enhance our understanding, let's convert the simplified fraction 4/25 into its decimal and percentage equivalents.
-
Decimal: To convert a fraction to a decimal, divide the numerator by the denominator: 4 ÷ 25 = 0.16.
-
Percentage: To convert a fraction to a percentage, multiply the decimal by 100: 0.16 x 100 = 16%.
Therefore, "20 of 125" represents 16% of the whole. This percentage representation provides a clear and easily interpretable measure of the part relative to the whole.
Real-World Applications: Putting it into Practice
The concept of "20 of 125" and its equivalent representations finds numerous applications across various fields:
-
Statistics and Probability: Imagine a survey where 20 out of 125 respondents answered "yes" to a particular question. The fraction 4/25, decimal 0.16, and percentage 16% all provide different ways to represent the proportion of "yes" responses. This data is crucial for understanding the overall sentiment and making informed decisions.
-
Business and Finance: In inventory management, if 20 out of 125 items are defective, the fraction 4/25 helps determine the defect rate. This information is vital for quality control and improving production processes. Similarly, in financial analysis, ratios are extensively used to assess the financial health of a company.
-
Science and Engineering: In scientific experiments, ratios and proportions are used extensively. For instance, if a chemical reaction requires a ratio of 20 parts of substance A to 125 parts of substance B, maintaining this precise ratio is crucial for the successful outcome of the experiment.
-
Everyday Life: Simple tasks like cooking or baking often involve ratios and proportions. Recipes frequently specify ratios of ingredients – for example, a recipe might call for 20 grams of sugar for every 125 grams of flour.
Solving Problems Using Proportions
Let's illustrate the use of proportions with a practical example:
A farmer harvests 125 apples, and 20 of them are rotten. If the farmer harvests 500 apples the following week, approximately how many rotten apples should they expect?
We can set up a proportion:
20 rotten apples / 125 total apples = x rotten apples / 500 total apples
To solve for x, we cross-multiply:
20 * 500 = 125 * x 10000 = 125x x = 10000 / 125 x = 80
Therefore, the farmer should expect approximately 80 rotten apples in the 500-apple harvest. This demonstrates how proportions can help predict outcomes based on established ratios.
Further Exploration: Expanding the Concept
The concept of "20 of 125" extends far beyond its basic representation. It introduces us to the broader world of:
-
Percentage Change: Understanding percentage change allows us to compare the difference between two values relative to the initial value. For example, if the number of rotten apples increased from 20 to 30, the percentage change would be calculated as follows: [(30-20)/20] x 100 = 50%.
-
Compound Proportions: These involve more than two ratios and are essential in solving complex problems involving multiple variables.
-
Inverse Proportions: In certain situations, two quantities are inversely proportional, meaning that as one increases, the other decreases.
Frequently Asked Questions (FAQ)
Q1: Can I simplify 20/125 any further than 4/25?
A1: No, 4/25 is the simplest form of the fraction because 4 and 25 share no common divisors other than 1.
Q2: What if the numbers weren't as easily divisible?
A2: If the numbers were larger or didn't share obvious common factors, you could use the Euclidean algorithm to find the greatest common divisor (GCD) and simplify the fraction efficiently.
Q3: Why is simplifying fractions important?
A3: Simplifying fractions makes calculations easier, provides a clearer representation of the proportion, and allows for easier comparison with other fractions or ratios.
Q4: What are some other ways to represent "20 of 125"?
A4: Besides fractions, decimals, and percentages, you can also represent it as a ratio (20:125), a part-to-whole statement ("20 out of 125"), or visually using a pie chart or bar graph.
Q5: How can I improve my understanding of fractions, ratios, and proportions?
A5: Practice is key! Solve various problems involving fractions, ratios, and proportions. Utilize online resources, textbooks, and educational videos to reinforce your understanding and build your problem-solving skills.
Conclusion: Mastering the Fundamentals
Understanding "20 of 125" – its representation as a fraction, ratio, proportion, decimal, and percentage – is a foundational step in mastering crucial mathematical concepts. Its real-world applications are extensive, spanning various fields from statistics and finance to science and everyday life. By grasping these fundamental concepts and practicing problem-solving, you will enhance your mathematical proficiency and develop critical thinking skills applicable across numerous disciplines. Remember that consistent practice and a willingness to explore different problem-solving approaches are essential for mastering fractions, ratios, and proportions. This deep dive into "20 of 125" has hopefully illuminated its significance and broadened your understanding of its underlying mathematical principles.
Latest Posts
Latest Posts
-
61kgs In Stone
Sep 13, 2025
-
Abcd Is Parallelogram
Sep 13, 2025
-
86kgs In Stone
Sep 13, 2025
-
14 30 Simplified
Sep 13, 2025
-
1050mm In Cm
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 20 Of 125 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.