23 X 5
stanleys
Sep 13, 2025 · 5 min read
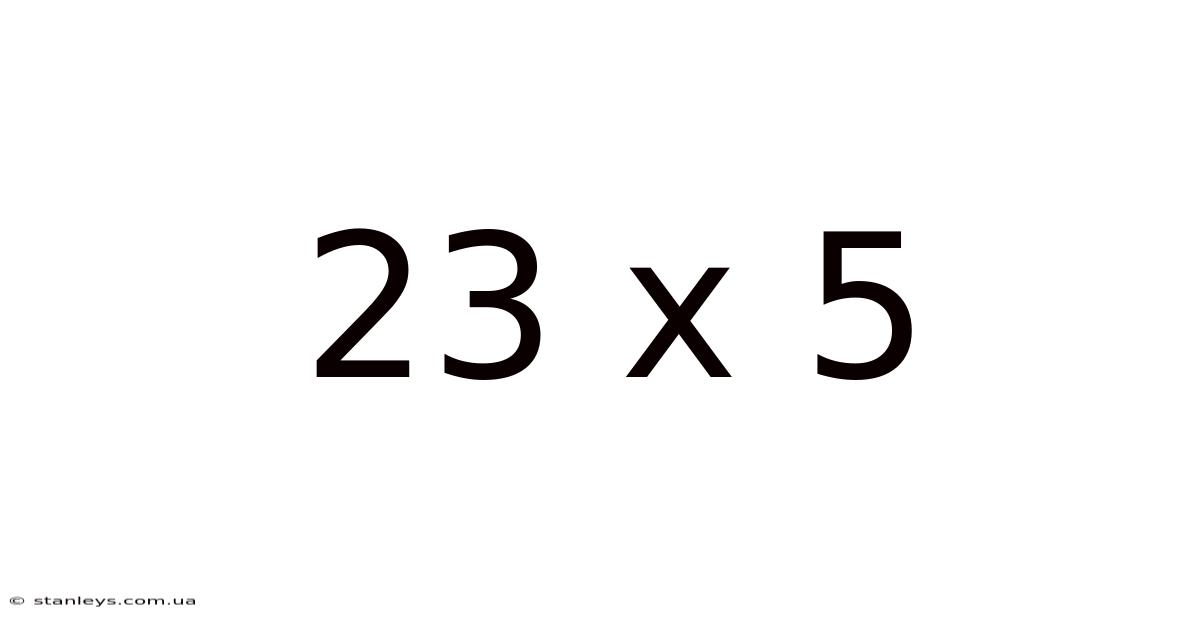
Table of Contents
Unveiling the Wonders of 23 x 5: A Deep Dive into Multiplication
This article explores the seemingly simple multiplication problem 23 x 5, delving far beyond the immediate answer. We'll unpack various methods of solving this problem, highlighting the underlying mathematical principles and exploring its applications in everyday life and advanced mathematical concepts. This journey will illuminate the beauty and power of mathematics, demonstrating how even the most basic calculations can reveal profound insights. The keyword here is multiplication, with semantic keywords including arithmetic, basic math, times tables, number sense, and mathematical operations.
Introduction: More Than Just an Answer
At first glance, 23 x 5 seems trivial. A quick calculation reveals the answer: 115. However, this seemingly simple equation provides a gateway to understanding fundamental mathematical concepts, problem-solving strategies, and even the historical development of numerical systems. We will delve into multiple approaches to solving this problem, demonstrating the versatility of mathematics and its applicability across various domains.
Method 1: The Standard Algorithm
The most common method taught in schools is the standard algorithm for multiplication. This involves multiplying each digit of the multiplicand (23) by the multiplier (5) separately, then adding the results.
- Step 1: Multiply the ones digit of 23 (3) by 5: 3 x 5 = 15. Write down 5 and carry-over 1.
- Step 2: Multiply the tens digit of 23 (2) by 5: 2 x 5 = 10. Add the carry-over 1: 10 + 1 = 11. Write down 11.
- Step 3: Combine the results: 115.
Therefore, 23 x 5 = 115. This method relies on the distributive property of multiplication, which states that a(b + c) = ab + ac. In this case, 5 x 23 = 5 x (20 + 3) = (5 x 20) + (5 x 3) = 100 + 15 = 115.
Method 2: Repeated Addition
Multiplication can be understood as repeated addition. 23 x 5 means adding 23 five times:
23 + 23 + 23 + 23 + 23 = 115
This method is helpful for visualizing multiplication and solidifying the concept for younger learners. It directly connects the abstract concept of multiplication to a concrete, repeatable action. This approach emphasizes the fundamental relationship between addition and multiplication.
Method 3: Using the Distributive Property Explicitly
As mentioned earlier, the distributive property is crucial to understanding multiplication. Let's break it down explicitly:
23 x 5 = (20 + 3) x 5 = (20 x 5) + (3 x 5) = 100 + 15 = 115
This method highlights the underlying mathematical principle and provides a more conceptual understanding of the process. It's particularly useful when dealing with larger numbers, as it breaks down the problem into smaller, more manageable parts.
Method 4: Breaking Down the Multiplier
Instead of breaking down the multiplicand (23), we can break down the multiplier (5):
23 x 5 = 23 x (2 + 3) = (23 x 2) + (23 x 3) = 46 + 69 = 115
This demonstrates the flexibility of the distributive property and shows that multiplication can be approached from multiple angles. This approach allows for a more flexible strategy, selecting factors that are easier to multiply mentally.
Method 5: Doubling and Halving
This technique is a mental math shortcut. We can double 23 to get 46, and halve 5 to get 2.5. Then, we multiply:
46 x 2.5 = 46 x (2 + 0.5) = (46 x 2) + (46 x 0.5) = 92 + 23 = 115
While involving decimals, this method illustrates the commutative property of multiplication (a x b = b x a) and provides a unique approach to problem-solving. This method is excellent for improving mental calculation skills and developing number sense.
The Significance of 115: Exploring Applications
The number 115 itself holds significance in various contexts. In mathematics, it's a composite number, divisible by 5, 23, and 1. It can be represented in different number systems (binary, hexadecimal, etc.). Beyond pure mathematics, 115 might represent:
- Quantities: 115 apples, 115 students, 115 kilometers, etc. – demonstrating its use in everyday counting and measurement.
- Units: 115 degrees Celsius, 115 square meters – showcasing its role in dimensional analysis.
- Abstract Concepts: In certain contexts, it could symbolize a quantity within a larger system or model.
Understanding the context in which 115 appears is crucial to interpreting its meaning and applying the mathematical knowledge gained.
Expanding the Scope: Beyond 23 x 5
The seemingly simple calculation of 23 x 5 opens the door to a much wider world of mathematical exploration. Here are some extensions:
- Larger Numbers: Applying the same methods to larger multiplication problems builds proficiency and reinforces the underlying principles.
- Algebra: The concept extends to algebraic expressions, where variables replace numbers, allowing for more generalized solutions. For example, solving for 'x' in the equation 5x = 115.
- Calculus: The principles of multiplication are fundamental to calculus, a branch of mathematics dealing with continuous change.
- Real-World Applications: From calculating areas and volumes to financial transactions and scientific modeling, multiplication is a cornerstone of many practical applications.
Frequently Asked Questions (FAQ)
Q: Why is learning multiplication important?
A: Multiplication is a fundamental building block of mathematics. It underpins more advanced concepts and is essential for problem-solving in various fields. Mastering multiplication improves number sense, mental math skills, and efficiency in calculations.
Q: What if I struggle with multiplication?
A: Don't be discouraged! Practice is key. Start with smaller numbers, gradually increasing the complexity. Use different methods and find the approach that works best for you. Seek help from teachers, tutors, or online resources.
Q: Are there any tricks to make multiplication easier?
A: Yes! There are numerous tricks and shortcuts for multiplication, such as using the distributive property, doubling and halving, or memorizing times tables. Explore various techniques to find what suits your learning style.
Q: How can I improve my mental math skills?
A: Consistent practice is crucial. Start with simple calculations and gradually increase the difficulty. Use flashcards, online games, or mental math exercises to challenge yourself regularly.
Conclusion: The Enduring Power of a Simple Equation
While 23 x 5 might seem like a rudimentary calculation, it serves as a potent illustration of fundamental mathematical principles. By exploring different methods and examining its various applications, we’ve expanded our understanding of multiplication beyond a simple answer. This exploration underscores the power and beauty of mathematics, reminding us that even the most basic concepts can reveal profound insights and have far-reaching implications. The journey from a simple multiplication problem to a deeper understanding of mathematical principles is a testament to the enduring value of mathematical exploration. The seemingly simple equation 23 x 5 is, in essence, a microcosm of the vast and fascinating world of mathematics.
Latest Posts
Latest Posts
-
61kgs In Stone
Sep 13, 2025
-
Abcd Is Parallelogram
Sep 13, 2025
-
86kgs In Stone
Sep 13, 2025
-
14 30 Simplified
Sep 13, 2025
-
1050mm In Cm
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 23 X 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.