64 Of 25
stanleys
Sep 16, 2025 · 6 min read
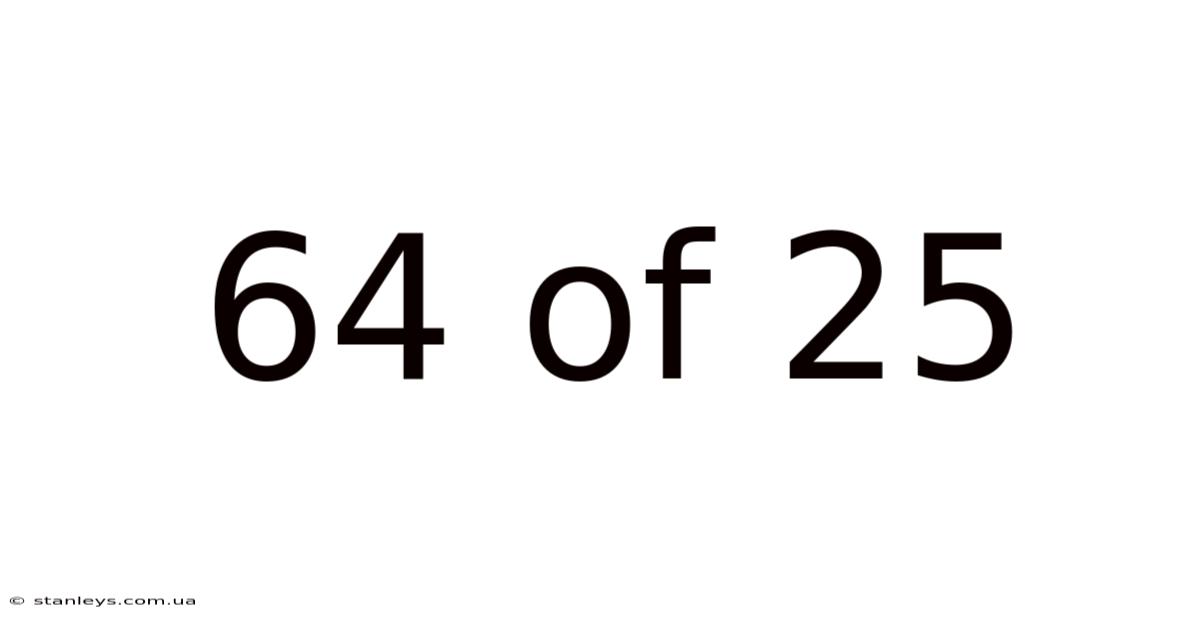
Table of Contents
Decoding the Fraction 64/25: A Deep Dive into Fractions, Decimals, and Percentages
Understanding fractions, decimals, and percentages is fundamental to numeracy. This article provides a comprehensive exploration of the fraction 64/25, covering its simplification, conversion to decimal and percentage forms, practical applications, and addressing common misconceptions. We'll delve into the underlying mathematical principles, making the concept accessible to learners of all levels. This detailed guide will equip you with a strong understanding of how to handle similar fractions and solidify your grasp of fundamental mathematical concepts.
1. Introduction: Understanding the Fraction 64/25
The fraction 64/25 represents 64 parts out of a total of 25 parts. This is an improper fraction because the numerator (64) is larger than the denominator (25). Improper fractions represent values greater than one. Understanding this basic concept is crucial before proceeding to more complex calculations. We will explore how to simplify this improper fraction, convert it to a decimal and percentage, and illustrate its practical application. This exploration will cover core mathematical principles, explaining each step clearly and concisely.
2. Simplifying the Fraction 64/25
While 64/25 is already in its simplest form in terms of integers (no common factors greater than 1), we can express it as a mixed number to better understand its magnitude. A mixed number combines a whole number and a proper fraction. To convert 64/25 to a mixed number, we perform long division:
64 ÷ 25 = 2 with a remainder of 14
Therefore, 64/25 can be written as 2 14/25. This representation clarifies that 64/25 is equal to two wholes and 14/25 of another whole. This form is often easier to visualize and work with in certain contexts.
3. Converting 64/25 to a Decimal
Converting a fraction to a decimal involves dividing the numerator by the denominator. In this case:
64 ÷ 25 = 2.56
Therefore, the decimal representation of 64/25 is 2.56. This decimal format is widely used in various applications, including calculations involving money, measurements, and data analysis.
4. Converting 64/25 to a Percentage
A percentage represents a fraction out of 100. To convert a decimal to a percentage, we multiply by 100 and add the percent symbol (%). Since we already know the decimal equivalent of 64/25 is 2.56:
2.56 x 100 = 256
Therefore, 64/25 is equal to 256%. This percentage representation is useful for expressing proportions and ratios in a readily understandable format. It clearly shows that 64/25 is significantly larger than 1 (or 100%).
5. Practical Applications of 64/25
The fraction 64/25, and its decimal and percentage equivalents, have practical applications across various fields. For example:
-
Finance: Imagine you invested $25 and earned a profit of $64. Your return on investment (ROI) would be 256%, calculated as (64/25) * 100.
-
Measurements: If you have a length of 25 units and need a length 64 units, you need 2.56 times the original length.
-
Data Analysis: If a survey showed 25 respondents and 64 expressed positive feedback, the positive response rate would be 256%. This highlights the importance of understanding the context; a percentage above 100% signifies that the value exceeds the reference point.
-
Recipe Scaling: If a recipe calls for 25 grams of an ingredient and you want to increase it to 64 grams, you would increase the recipe's scale by a factor of 2.56.
6. Understanding Improper Fractions and their Conversions
As mentioned, 64/25 is an improper fraction. These fractions are essential for representing quantities larger than one whole. Their conversion to mixed numbers and decimals is vital for practical calculations. The process, as shown above, involves division. Let's illustrate with another example:
Consider the fraction 17/5. Dividing 17 by 5 gives 3 with a remainder of 2. Therefore, 17/5 as a mixed number is 3 2/5, and as a decimal is 3.4.
7. Common Misconceptions about Fractions, Decimals, and Percentages
Several common misconceptions surround these related concepts:
-
Thinking percentages must be between 0% and 100%: Percentages can exceed 100%, representing values greater than the whole, as shown by our example of 64/25 being 256%.
-
Difficulty converting between forms: The processes of converting between fractions, decimals, and percentages are straightforward, involving division and multiplication by 100. Practice helps to solidify these conversions.
-
Ignoring the importance of simplification: While not crucial in all cases, simplifying fractions (where possible) can make calculations easier and results more manageable.
-
Misinterpreting mixed numbers: Understanding that a mixed number represents a whole number and a fractional part is key to accurate calculations.
8. Further Exploration: Working with Other Fractions
The principles applied to 64/25 are applicable to any fraction. To solidify your understanding, consider practicing with other improper fractions, such as 37/10, 51/8, or 105/22. Follow the same steps:
-
Identify the type of fraction (proper or improper): Improper fractions are greater than 1.
-
Convert to a mixed number (if improper): Use long division to find the whole number part and the remaining fraction.
-
Convert to decimal: Divide the numerator by the denominator.
-
Convert to percentage: Multiply the decimal by 100 and add the % symbol.
9. Frequently Asked Questions (FAQ)
-
Q: What is the simplest form of 64/25?
-
A: While 64 and 25 share no common factors other than 1, the simplest form in terms of a mixed number is 2 14/25.
-
Q: Can a percentage be greater than 100%?
-
A: Yes, a percentage greater than 100% represents a value that exceeds the whole.
-
Q: How do I convert a mixed number back to an improper fraction?
-
A: Multiply the whole number by the denominator and add the numerator. This becomes the new numerator, while the denominator remains the same. For example, 3 2/5 becomes (3*5 + 2)/5 = 17/5.
-
Q: What is the significance of understanding improper fractions?
-
A: Improper fractions are essential for representing quantities larger than one whole and are crucial for many mathematical calculations and real-world applications.
10. Conclusion: Mastering Fractions, Decimals, and Percentages
This in-depth exploration of the fraction 64/25 has provided a robust understanding of its various forms, its practical applications, and the fundamental concepts of fractions, decimals, and percentages. Mastering these concepts is critical for success in mathematics and numerous other fields. By understanding the conversion processes and addressing common misconceptions, you've significantly expanded your mathematical skills. Remember that consistent practice and application are key to solidifying your understanding. Continue exploring different fractions and apply the principles learned here to various problems. With persistent effort, you will confidently navigate the world of numbers and their representations.
Latest Posts
Related Post
Thank you for visiting our website which covers about 64 Of 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.