X 6 2
stanleys
Sep 16, 2025 · 6 min read
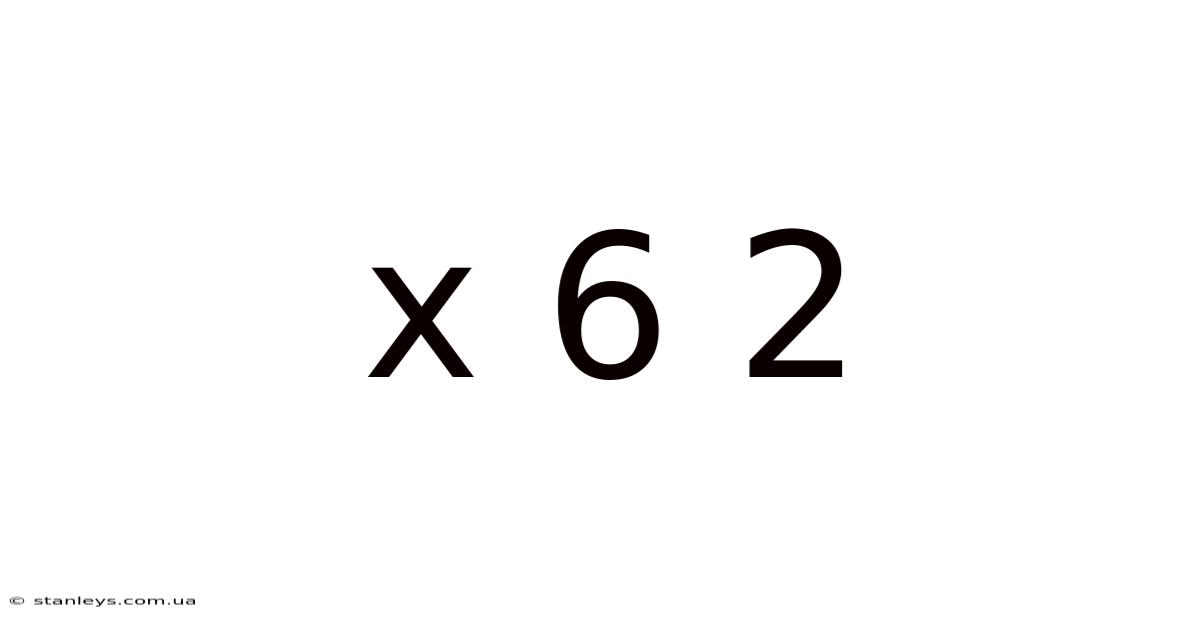
Table of Contents
Decoding the Enigma: A Deep Dive into x⁶ + 2
This article explores the mathematical enigma presented by the expression x⁶ + 2, delving into its properties, potential solutions, and the broader mathematical concepts it touches upon. We'll unravel its complexities, examining its behavior across different number systems and highlighting the fascinating challenges it poses for mathematicians and students alike. Understanding this seemingly simple expression unlocks deeper insights into algebra, number theory, and the elegance of mathematical structures.
Introduction: The Allure of Simplicity and Complexity
At first glance, x⁶ + 2 appears deceptively simple. It's a polynomial expression, a fundamental building block in algebra. Yet, its seemingly straightforward nature hides a surprising depth of mathematical richness. The challenge lies not just in finding its roots (the values of x that make the expression equal to zero), but also in understanding its behavior, its relationship to other mathematical concepts, and the techniques required to analyze it effectively. This exploration will delve into various approaches, ranging from basic algebraic manipulation to more advanced techniques, shedding light on the intricacies of this seemingly simple expression.
Exploring Solutions: A Journey Through Number Systems
Finding the roots of x⁶ + 2, or solving the equation x⁶ + 2 = 0, requires us to consider different number systems.
-
Real Numbers: In the realm of real numbers, there are no real solutions to this equation. This is because x⁶ is always non-negative (positive or zero) for any real number x. Adding 2 to a non-negative number will always result in a positive number, making it impossible for the expression to equal zero.
-
Complex Numbers: The situation changes dramatically when we expand our search to the realm of complex numbers. Complex numbers encompass real numbers and imaginary numbers (multiples of the imaginary unit i, where i² = -1). To find the roots, we can rewrite the equation as:
x⁶ = -2
We can express -2 in polar form as 2 * e^(iπ), where e is Euler's number (approximately 2.71828) and π is pi (approximately 3.14159). Using De Moivre's theorem, we can find the six complex roots:
xₖ = ⁶√2 * e^(i(π + 2kπ)/6) where k = 0, 1, 2, 3, 4, 5
This formula generates six distinct complex roots, each representing a solution to the equation x⁶ + 2 = 0. These roots are symmetrically distributed around the origin in the complex plane.
-
Other Number Systems: The exploration can extend to other number systems, such as quaternions or other algebraic structures. The solutions and their properties will vary depending on the chosen number system and its inherent rules of operation.
Applying Algebraic Techniques: Factoring and Manipulation
While finding the complex roots directly using De Moivre's theorem is efficient, exploring alternative algebraic approaches can offer valuable insights. Unfortunately, x⁶ + 2 resists straightforward factoring using typical algebraic techniques. There's no simple way to break it down into smaller, easily solvable expressions. This highlights the limitations of basic algebraic manipulation in certain cases and emphasizes the need for more advanced methods.
The Role of Number Theory: Exploring Divisibility and Congruences
Number theory provides a powerful lens for examining the properties of x⁶ + 2. For example, considering the expression modulo different integers can reveal interesting patterns and constraints on potential solutions. Modulo arithmetic, where we are only concerned with remainders after division, can help simplify the analysis.
Advanced Mathematical Concepts: Galois Theory and Beyond
The equation x⁶ + 2 = 0 involves concepts that are often studied within the realm of Galois theory. Galois theory deals with the symmetries of polynomial equations and their solutions. The specific structure of the Galois group associated with this equation provides information about the solvability of the equation using radicals. The complexity of the Galois group suggests that there's no simple radical expression for the roots, reinforcing the need for complex numbers and more sophisticated techniques like De Moivre's theorem.
Applications and Connections: Where Does it Matter?
While the equation x⁶ + 2 = 0 might seem abstract, it connects to broader mathematical concepts with practical applications:
-
Abstract Algebra: Understanding the properties of this equation enhances the understanding of abstract algebraic structures and group theory. The analysis contributes to the broader field of abstract algebra, crucial for advanced mathematical research.
-
Complex Analysis: The exploration of complex roots provides a good example of the power and necessity of extending the number system to solve equations that are unsolvable within the real number system. It showcases crucial aspects of complex analysis, with applications in various fields like engineering and physics.
-
Numerical Analysis: Even if we can't find exact solutions easily, numerical methods can approximate the roots to any desired degree of accuracy. This has practical value in numerous applications where approximate solutions are sufficient.
Frequently Asked Questions (FAQ)
Q: Can x⁶ + 2 be factored easily?
A: No, x⁶ + 2 does not factor easily using standard algebraic techniques. It resists simple factoring methods.
Q: Are there any real solutions to x⁶ + 2 = 0?
A: No, there are no real solutions. x⁶ is always non-negative, so x⁶ + 2 is always positive.
Q: How many complex roots does x⁶ + 2 = 0 have?
A: It has six distinct complex roots. This is a consequence of the Fundamental Theorem of Algebra, which states that a polynomial of degree n has exactly n roots (counting multiplicity) in the complex numbers.
Q: What is De Moivre's Theorem, and why is it important here?
A: De Moivre's theorem provides a way to compute powers and roots of complex numbers expressed in polar form. It's crucial for finding the complex roots of x⁶ + 2 = 0 efficiently.
Q: What is the significance of the Galois group in this context?
A: The Galois group associated with x⁶ + 2 = 0 provides insights into the symmetries of the equation and its roots, influencing how solvable it is using radicals. The complex nature of the Galois group here reflects the need for more advanced methods to find the solutions.
Conclusion: Beyond the Surface
The seemingly simple expression x⁶ + 2 reveals a surprising depth of mathematical complexity. Exploring its solutions requires venturing into the realm of complex numbers and utilizing techniques like De Moivre's theorem. The journey highlights the interconnectedness of different mathematical fields, showcasing the elegance and power of algebra, number theory, and Galois theory. By dissecting this equation, we’ve not only found its roots but also gained a deeper appreciation for the intricate beauty hidden within seemingly straightforward mathematical expressions. The exploration serves as a testament to the ongoing quest for understanding the fundamental principles that govern the mathematical world. Further research could involve exploring the behavior of similar expressions, extending the analysis to even more complex number systems, and examining the broader implications within various fields of mathematics and its applications.
Latest Posts
Related Post
Thank you for visiting our website which covers about X 6 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.