25 Of 450
stanleys
Sep 16, 2025 · 6 min read
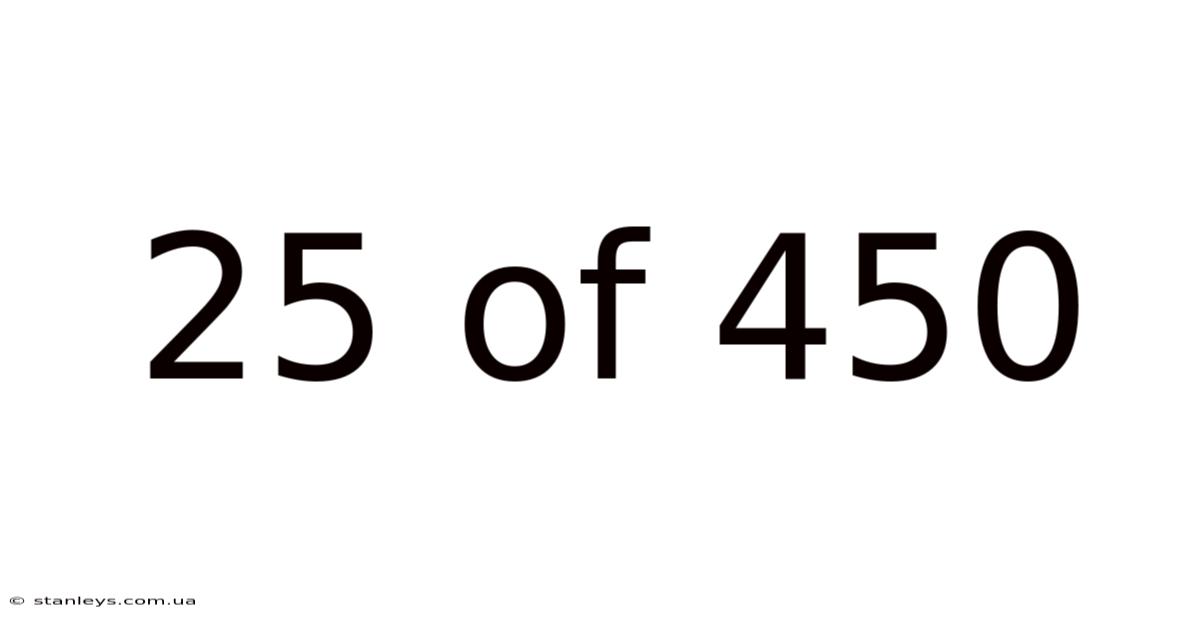
Table of Contents
Understanding the Fraction 25/450: A Deep Dive into Simplification and Applications
This article explores the fraction 25/450, demonstrating how to simplify it to its lowest terms, understanding its decimal and percentage equivalents, and exploring its practical applications in various contexts. We will delve into the mathematical concepts behind fraction simplification and show you how to apply these principles to other fractions. This comprehensive guide is perfect for students learning fractions, teachers needing supplemental material, or anyone interested in improving their mathematical understanding. We will also tackle common questions and misconceptions surrounding fractions.
Introduction: The Significance of Simplifying Fractions
Fractions represent parts of a whole. The fraction 25/450 signifies 25 parts out of a total of 450 parts. While this representation is accurate, it's not always the most efficient or easily understandable form. Simplifying a fraction, also known as reducing a fraction, means finding an equivalent fraction where the numerator (top number) and the denominator (bottom number) are smaller, but the fraction represents the same value. This simplification makes the fraction easier to work with in calculations and provides a clearer understanding of its magnitude. The ability to simplify fractions is a fundamental skill in mathematics, with applications ranging from basic arithmetic to advanced calculus.
Simplifying 25/450: A Step-by-Step Guide
Simplifying 25/450 involves finding the greatest common divisor (GCD) of both the numerator (25) and the denominator (450). The GCD is the largest number that divides both 25 and 450 without leaving a remainder.
Step 1: Find the Factors
Let's list the factors of 25 and 450:
- Factors of 25: 1, 5, 25
- Factors of 450: 1, 2, 3, 5, 6, 9, 10, 15, 18, 25, 30, 45, 50, 75, 90, 150, 225, 450
Step 2: Identify the Greatest Common Divisor (GCD)
By comparing the lists, we see that the largest number that divides both 25 and 450 is 25. Therefore, the GCD of 25 and 450 is 25.
Step 3: Divide the Numerator and Denominator by the GCD
To simplify the fraction, we divide both the numerator and the denominator by the GCD (25):
25 ÷ 25 = 1 450 ÷ 25 = 18
Therefore, the simplified form of 25/450 is 1/18.
Understanding Equivalent Fractions
It's important to understand that 25/450 and 1/18 are equivalent fractions. They represent the same proportion or value. This means that if you were to divide a pie into 450 equal slices and take 25, it would be the same as dividing a pie into 18 equal slices and taking 1.
Decimal and Percentage Equivalents
To further understand the value of 1/18, let's convert it to its decimal and percentage equivalents:
Decimal Equivalent:
To convert a fraction to a decimal, divide the numerator by the denominator:
1 ÷ 18 ≈ 0.0556
Percentage Equivalent:
To convert a decimal to a percentage, multiply by 100:
0.0556 × 100 ≈ 5.56%
Therefore, 25/450 is approximately equal to 0.0556 or 5.56%.
Practical Applications of 25/450 (or 1/18)
The fraction 1/18, the simplified form of 25/450, can be applied in various real-world scenarios:
- Proportions and Ratios: If you have a group of 18 people and one person is selected, this represents 1/18 of the group.
- Percentage Calculations: Calculating 5.56% of a quantity is equivalent to calculating 1/18 of that quantity. For example, finding 5.56% of a $1000 investment would be (1/18) * $1000 = $55.56 (approximately).
- Measurement Conversions: Imagine a recipe that calls for 1/18 of a cup of flour. This would require precise measurement.
- Probability: If there's a 1 in 18 chance of an event occurring, this can be represented by the fraction 1/18.
Explaining Fraction Simplification to Beginners
Teaching children about fraction simplification requires a clear and engaging approach. Here's a step-by-step guide:
-
Visual Aids: Use visual aids like pizzas or chocolate bars to demonstrate how fractions work. Dividing a pizza into 450 slices and taking 25 is visually complex; showing the equivalent 1/18 is much simpler.
-
Real-World Examples: Relate fractions to real-world situations children can understand, such as sharing cookies or toys.
-
Step-by-Step Approach: Break down the simplification process into manageable steps, as demonstrated earlier in this article.
-
Practice: Provide ample practice problems with varying levels of difficulty.
Advanced Concepts: Finding the GCD Efficiently
While listing factors is a viable method for smaller numbers, it becomes less efficient for larger numbers. The Euclidean algorithm provides a more efficient method for finding the GCD of two numbers:
- Divide the larger number by the smaller number and find the remainder.
- Replace the larger number with the smaller number and the smaller number with the remainder.
- Repeat steps 1 and 2 until the remainder is 0.
- The last non-zero remainder is the GCD.
Let's apply this to 25 and 450:
- 450 ÷ 25 = 18 with a remainder of 0. Since the remainder is 0, the GCD is the last non-zero remainder, which was 25 in the previous method (where we directly identified the GCD).
Frequently Asked Questions (FAQ)
Q1: Why is simplifying fractions important?
A1: Simplifying fractions makes them easier to understand, compare, and use in calculations. It also presents the fraction in its most concise and efficient form.
Q2: What happens if I simplify a fraction incorrectly?
A2: If you simplify a fraction incorrectly, you'll end up with a fraction that is not equivalent to the original fraction, leading to inaccurate calculations and results.
Q3: Can all fractions be simplified?
A3: No. Some fractions, like 1/17 or 7/11, are already in their simplest form because the numerator and denominator share no common factors other than 1.
Q4: What if the GCD is 1?
A4: If the GCD of the numerator and denominator is 1, the fraction is already in its simplest form.
Conclusion: Mastering Fraction Simplification
Understanding and applying fraction simplification is a critical skill in mathematics. The fraction 25/450, simplified to 1/18, serves as an excellent example to illustrate the process and its importance. Through this detailed explanation, encompassing simplification techniques, decimal and percentage conversions, and real-world applications, we've aimed to provide a comprehensive understanding of this fundamental mathematical concept. Remember, consistent practice is key to mastering fraction simplification and enhancing your overall mathematical abilities. The ability to work confidently with fractions is essential for progress in higher-level mathematics and problem-solving in numerous fields. From baking to engineering, understanding fractions is a building block for success.
Latest Posts
Related Post
Thank you for visiting our website which covers about 25 Of 450 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.