63 X 2
stanleys
Sep 13, 2025 · 6 min read
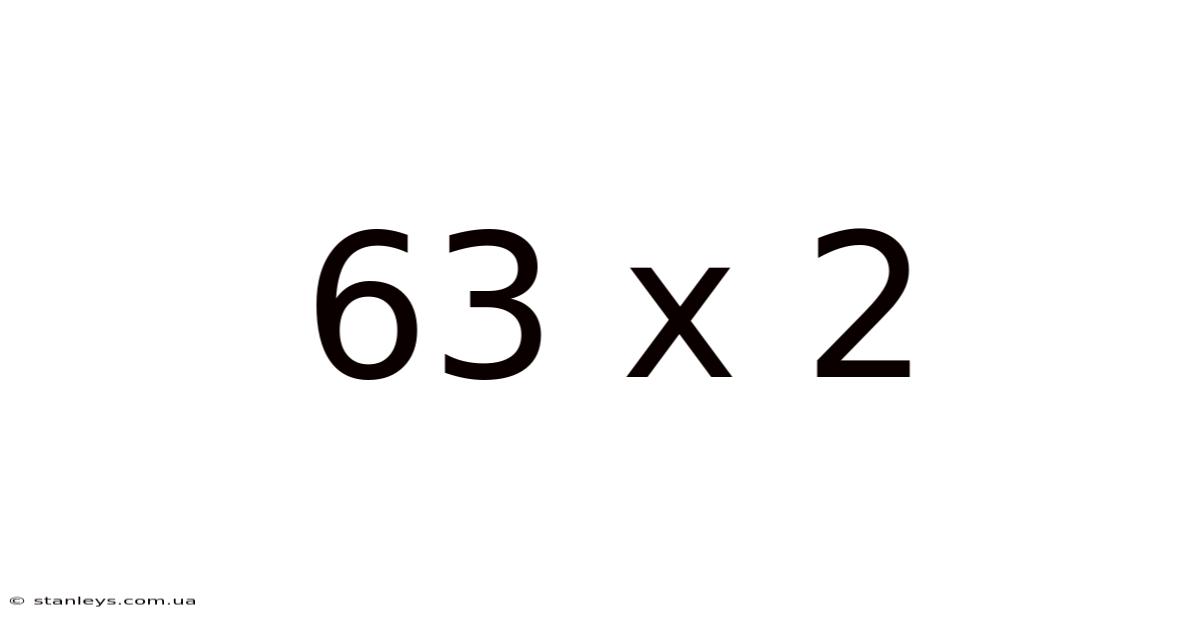
Table of Contents
Decoding 63 x 2: A Deep Dive into Multiplication and its Applications
This article explores the seemingly simple calculation of 63 multiplied by 2, delving far beyond the immediate answer. We'll uncover the fundamental principles of multiplication, explore different methods for solving this problem, and examine its broader applications in various fields. This exploration will cater to all levels, from elementary school students grasping the basics to those seeking a deeper understanding of mathematical concepts. We will cover everything from basic arithmetic to the more advanced concepts underlying this simple equation.
Introduction: Understanding Multiplication
Multiplication is a fundamental arithmetic operation representing repeated addition. It's a concise way of adding a number to itself a specific number of times. For instance, 63 x 2 means adding 63 to itself twice: 63 + 63. While this example seems straightforward, understanding the underlying principles is crucial for tackling more complex mathematical problems later on. This simple equation forms the bedrock of many advanced mathematical concepts, from algebra to calculus. This deep dive will highlight its significance and broader implications.
Method 1: Traditional Multiplication
The most common method taught in schools involves breaking down the numbers and multiplying them digit by digit. Let's apply this method to solve 63 x 2:
- Multiply the ones digit: 2 x 3 = 6. Write down '6' in the ones place.
- Multiply the tens digit: 2 x 6 = 12. Write down '12' to the left of the '6'.
- Combine the results: The answer is 126.
Therefore, 63 x 2 = 126. This seemingly simple process forms the foundation for more complex multiplications, which are the basis for solving more complex problems involving large numbers. This traditional method is valuable for developing a strong understanding of place value and the distributive property.
Method 2: Doubling and Decomposition
This method involves doubling the number 63. While seemingly similar to the previous method, it offers a different approach to understanding multiplication, especially useful for mental math and grasping concepts of number relationships.
We can think of 63 as (60 + 3). Doubling each component independently, we have:
- 2 x 60 = 120
- 2 x 3 = 6
Adding these results together: 120 + 6 = 126. This method highlights the distributive property of multiplication, where multiplying a sum by a number is the same as multiplying each addend by the number and then adding the products. This understanding is crucial for further mathematical development.
Method 3: Visual Representation – Using Arrays
Visual aids can significantly enhance understanding, particularly for younger learners. We can represent 63 x 2 using an array:
Imagine a rectangle with 63 squares in one row. Now, add another identical row beneath it. You'll have a total of 126 squares. This visual representation makes the concept of repeated addition tangible and easy to grasp. This is especially helpful for building a foundational understanding of multiplication before moving on to abstract calculations. This reinforces the connection between the abstract concept of multiplication and its concrete application.
Method 4: Using the Number Line
A number line can offer a visual representation of the repeated addition inherent in multiplication. Starting at 0, jump 63 units to the right, then jump another 63 units. You will land on 126, demonstrating that 63 x 2 = 126 visually. This method provides a spatial understanding of the process, making it intuitive and concrete. The use of visual aids can be particularly effective in making complex concepts more accessible.
The Distributive Property in Action
The distributive property is crucial to understanding multiplication, particularly with larger numbers. It states that a(b + c) = ab + ac. In our example:
2 x 63 = 2 x (60 + 3) = (2 x 60) + (2 x 3) = 120 + 6 = 126.
This principle underpins many mathematical operations and is fundamental to algebraic manipulation. It shows that multiplication can be broken down into simpler steps making complex calculations more manageable. This demonstrates the power and flexibility of the distributive property in simplifying calculations.
Applications of 63 x 2 and Multiplication in Real Life
While seemingly simple, the concept of multiplication, and specifically the equation 63 x 2, has numerous real-world applications:
- Shopping: Calculating the total cost of two identical items priced at $63 each.
- Measurement: Determining the total length of two pieces of wire, each measuring 63 centimeters.
- Cooking: Doubling a recipe that calls for 63 grams of flour.
- Construction: Calculating the total area of two identical rooms measuring 63 square feet each.
- Finance: Calculating the total earnings from two investments each yielding $63.
These examples demonstrate the practical significance of understanding multiplication in everyday life, highlighting its role in a variety of contexts. The simplicity of 63 x 2 belies its extensive applicability across various domains.
Beyond the Basics: Expanding Our Understanding
The calculation 63 x 2 serves as a springboard to explore more advanced mathematical concepts:
- Algebra: The equation can be represented algebraically as 2x = 126, where x represents the unknown number (63). Solving for x involves division, another fundamental arithmetic operation.
- Geometry: Calculating the area of a rectangle with dimensions 63 units by 2 units.
- Number Theory: Exploring the factors and multiples of 126. This leads to understanding concepts like prime factorization and divisibility rules.
These extensions demonstrate that even the simplest arithmetic problems are connected to more complex mathematical concepts.
Frequently Asked Questions (FAQ)
-
Q: What is the quickest way to calculate 63 x 2?
- A: The traditional multiplication method or the doubling method are both efficient. For mental math, the doubling method (doubling 63) might be faster.
-
Q: Why is it important to learn multiplication?
- A: Multiplication is a fundamental building block for more advanced mathematics and crucial for problem-solving in many real-world situations.
-
Q: Are there other ways to solve 63 x 2 besides the ones mentioned?
- A: While the methods described are the most common and efficient, there might be other creative approaches using different mathematical properties or tools.
-
Q: How can I improve my multiplication skills?
- A: Practice regularly, use different methods, and try solving multiplication problems in various contexts.
-
Q: What if I am struggling with multiplication?
- A: Seek help from a teacher, tutor, or utilize online resources to understand the underlying concepts and practice more.
Conclusion: The Significance of a Simple Calculation
The seemingly simple calculation of 63 x 2 holds much greater significance than its immediate answer of 126. It's a gateway to understanding the fundamental principles of multiplication, the power of different calculation methods, and the vast applications of this operation in various fields. By exploring this simple equation in depth, we've demonstrated the interconnectedness of mathematical concepts and emphasized the importance of understanding the 'why' behind the 'how'. Mastering fundamental arithmetic operations like multiplication is crucial for building a solid foundation for more advanced mathematical pursuits and navigating everyday challenges. From basic arithmetic to more advanced applications, 63 x 2 serves as a microcosm of mathematical understanding, demonstrating the profound implications of seemingly simple calculations. Continuous learning and exploration of mathematical concepts are crucial for expanding knowledge and tackling complex problems in the future.
Latest Posts
Latest Posts
-
23 X 5
Sep 13, 2025
-
20 Of 125
Sep 13, 2025
-
38 5celsius To Fahrenheit
Sep 13, 2025
-
143 Pounds Kg
Sep 13, 2025
-
124 Lbs Kg
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 63 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.