6 X -2
stanleys
Sep 12, 2025 · 5 min read
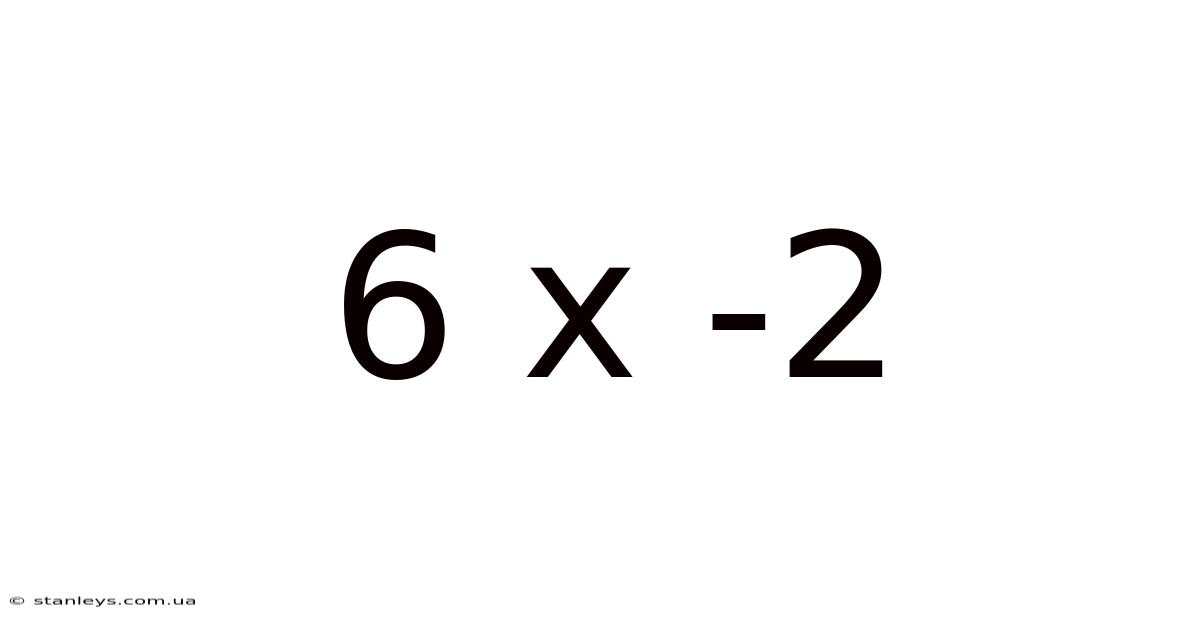
Table of Contents
Decoding 6x - 2: A Deep Dive into Linear Equations
This article provides a comprehensive exploration of the algebraic expression "6x - 2," covering its fundamental components, practical applications, and deeper mathematical concepts related to linear equations. Understanding this seemingly simple expression unlocks a gateway to a broader understanding of algebra and its real-world implications. We will delve into its structure, explore methods for solving related equations, and examine its graphical representation, all while maintaining a friendly and accessible approach.
Understanding the Basics: Components of 6x - 2
At its core, "6x - 2" is a linear algebraic expression. Let's break down its components:
-
6: This is the coefficient of the variable 'x'. It represents a multiplicative factor; we're multiplying 'x' by 6.
-
x: This is the variable. In mathematics, a variable represents an unknown quantity or a value that can change. 'x' is a common placeholder for variables.
-
-: This is the subtraction operator. It indicates that we are subtracting 2 from the product of 6 and x.
-
2: This is the constant term. It's a fixed numerical value that does not change.
Together, these components create a simple yet powerful expression that forms the basis for many algebraic equations and problems.
Solving Equations Involving 6x - 2
The expression "6x - 2" becomes incredibly useful when incorporated into equations. An equation is a mathematical statement asserting the equality of two expressions. Let's examine a few scenarios and how to solve them:
Scenario 1: Finding x when 6x - 2 = 10
This equation asks us to find the value of 'x' that makes the equation true. To solve it, we use the principles of algebraic manipulation:
-
Add 2 to both sides: This isolates the term containing 'x'. The equation becomes: 6x = 12
-
Divide both sides by 6: This solves for 'x'. The equation becomes: x = 2
Therefore, when x = 2, the equation 6x - 2 = 10 holds true.
Scenario 2: Solving for x when 6x - 2 = -8
Following the same principles:
-
Add 2 to both sides: 6x = -6
-
Divide both sides by 6: x = -1
In this case, x = -1 satisfies the equation 6x - 2 = -8.
Scenario 3: A More Complex Equation: 2(3x - 1) = 6x - 2
This equation introduces parentheses, requiring us to simplify before solving:
- Distribute the 2: The equation becomes 6x - 2 = 6x - 2
Notice that both sides are identical. This means the equation is true for any value of x. Such equations are called identities.
Scenario 4: An Equation with No Solution: 6x - 2 = 6x + 4
Let's try to solve this:
- Subtract 6x from both sides: This leaves us with -2 = 4
This is a false statement. There is no value of x that can make this equation true. This equation has no solution.
Graphical Representation of 6x - 2
The expression 6x - 2 represents a linear function. Linear functions, when graphed, produce straight lines. To graph this function, we can create a table of values:
| x | 6x - 2 | y |
|---|---|---|
| -2 | -14 | -14 |
| -1 | -8 | -8 |
| 0 | -2 | -2 |
| 1 | 4 | 4 |
| 2 | 10 | 10 |
Plotting these points (x, y) on a coordinate plane and connecting them will result in a straight line with a slope of 6 and a y-intercept of -2. The slope represents the rate of change of the function, while the y-intercept is the point where the line crosses the y-axis (when x = 0).
Real-World Applications
Linear equations, like those based on the expression 6x - 2, have countless applications in real-world scenarios:
-
Calculating Costs: Imagine a phone plan with a $2 monthly fee and a cost of $6 per gigabyte of data used. The total cost (y) can be represented by the equation y = 6x - 2, where x is the number of gigabytes used.
-
Analyzing Profit: A business might use a similar equation to model its profit, where 'x' represents the number of units sold, and the expression reflects the revenue minus expenses.
-
Modeling Physical Phenomena: In physics, linear equations can describe the relationship between distance, speed, and time.
-
Predictive Modeling: Linear equations form the foundation of many statistical models used for forecasting and prediction in various fields.
Explanation of the Scientific Principles
The expression 6x - 2 is fundamentally based on the principles of:
-
Algebra: The manipulation of variables and constants according to established rules to solve equations.
-
Linearity: The relationship between variables is linear, meaning a constant change in one variable results in a proportional change in the other. This is evident in the straight-line graph.
-
Functions: The expression defines a function that maps input values (x) to output values (y).
Frequently Asked Questions (FAQ)
Q: What is the difference between an expression and an equation?
A: An expression is a combination of numbers, variables, and operators. An equation is a statement that asserts the equality of two expressions.
Q: How can I check if my solution to an equation is correct?
A: Substitute your solution back into the original equation. If the equation holds true, your solution is correct.
Q: What if I have an equation with more than one variable?
A: Equations with more than one variable require additional information (another equation, for example) to solve for specific values.
Q: What are some common mistakes when solving linear equations?
A: Common mistakes include incorrect application of the order of operations (PEMDAS/BODMAS), errors in adding or subtracting terms, and forgetting to perform the same operation on both sides of the equation.
Conclusion
The simple expression "6x - 2" serves as a powerful introduction to the world of algebra and linear equations. Understanding its components, how to solve related equations, and its graphical representation is crucial for anyone pursuing further studies in mathematics or related fields. From calculating costs to modeling complex systems, the applications are far-reaching. Mastering this foundational concept empowers you to tackle more complex mathematical challenges and to understand and interpret the world around you in a more quantitative manner. By actively engaging with the concepts presented here, you'll solidify your understanding and build a strong foundation for future mathematical endeavors. Remember to practice regularly, and don't hesitate to seek clarification when needed. With persistent effort, you'll confidently navigate the fascinating world of algebra.
Latest Posts
Latest Posts
-
3x 2 X
Sep 12, 2025
-
1 9 Squared
Sep 12, 2025
-
140 In Kilograms
Sep 12, 2025
-
90lb In Stone
Sep 12, 2025
-
10 Of 600
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 6 X -2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.