3x 2 X
stanleys
Sep 12, 2025 · 7 min read
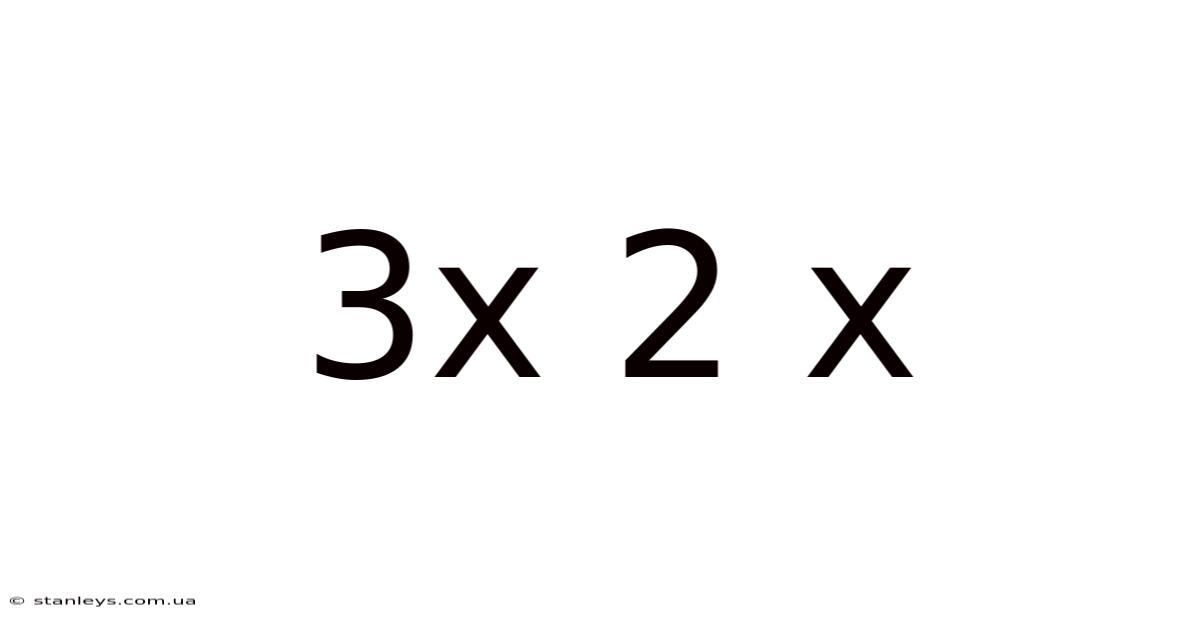
Table of Contents
Decoding 3 x 2 x: Unveiling the Mysteries of Tensor Products and Their Applications
The expression "3 x 2 x" might seem deceptively simple at first glance. It evokes images of basic multiplication, perhaps hinting at a simple calculation resulting in 6. However, depending on the context, this seemingly straightforward notation can represent something far more profound and powerful: the tensor product. This article will delve into the meaning of 3 x 2 x, exploring its significance within the realms of linear algebra, tensor calculus, and its numerous applications across diverse fields. We will move beyond the basic arithmetic interpretation and uncover the rich mathematical structure hidden within this compact notation.
Understanding the Basics: From Scalars to Vectors to Tensors
Before embarking on a journey into the complexities of tensor products, let's establish a firm foundation by understanding the fundamental building blocks: scalars, vectors, and tensors themselves.
-
Scalars: These are simply single numbers, like 3, -2, or π. They represent magnitude without direction.
-
Vectors: Vectors, often represented as columns or rows of numbers (e.g., [1, 2, 3]), possess both magnitude and direction. They are fundamental in representing quantities like force, velocity, or displacement. The number of elements in a vector defines its dimension (a 3-dimensional vector has three components).
-
Tensors: Tensors generalize the concepts of scalars and vectors. A scalar can be considered a 0-order tensor, a vector a 1-order tensor. Higher-order tensors extend this concept. A 2-order tensor (like a matrix) can be visualized as a table of numbers, with rows and columns. A 3-order tensor adds another dimension, often visualized as a cube of numbers, and so on. Tensors are essential for representing multi-dimensional relationships and transformations.
The Tensor Product: More Than Just Multiplication
Now, let's return to "3 x 2 x." In the context of tensor products, this notation doesn't represent simple scalar multiplication. Instead, it often describes the dimensions of the resulting tensor from the product of two tensors. Specifically, it suggests that we're dealing with tensors having dimensions 3 and 2, resulting in a tensor with dimensions implicitly defined by the "x" – which signifies the tensor product operation. This operation combines the information contained in two tensors in a structured way.
The most straightforward example is the tensor product of two vectors. Consider a 3-dimensional vector u and a 2-dimensional vector v:
u = [u₁, u₂, u₃] v = [v₁, v₂]
Their tensor product, denoted as u ⊗ v, results in a 3 x 2 matrix:
u ⊗ v = [[u₁v₁, u₁v₂], [u₂v₁, u₂v₂], [u₃v₁, u₃v₂]]
Notice how each element of u is multiplied by each element of v, systematically populating the resulting matrix. This structured multiplication is the essence of the tensor product. It's not simply multiplying corresponding elements; it's a carefully orchestrated combination creating a higher-dimensional structure.
Generalizing the Tensor Product: Higher-Order Tensors
The power of the tensor product lies in its ability to handle tensors of any order. The notation "3 x 2 x" can be interpreted in various ways depending on the context. For instance:
-
Product of two matrices: If we have a 3 x m matrix (A) and an m x 2 matrix (B), their product (A x B) is a 3 x 2 matrix. While not strictly a tensor product in the purest mathematical sense, it exhibits similar dimensional characteristics.
-
Tensor product of a vector and a matrix: A 3-dimensional vector tensored with a 2 x n matrix would yield a 3 x 2 x n tensor (a three-dimensional array). This generalizes the vector-vector product shown above.
-
Tensor product of two higher-order tensors: The notation could also represent the dimensions of a resulting tensor from the product of two higher-order tensors (e.g., a 3 x 2 x p tensor multiplied by a p x q x r tensor, resulting in a potentially higher-dimensional tensor with dimensions determined by the rules of tensor multiplication).
The key idea is that the "x" always signifies a structured combination, not a simple element-wise multiplication. The dimensionality of the resulting tensor is systematically constructed based on the dimensions of the input tensors.
Mathematical Formalism and Properties
Let's delve a bit deeper into the mathematical formalism surrounding the tensor product. Given two vector spaces V and W, their tensor product, denoted as V ⊗ W, is a new vector space whose elements are linear combinations of tensor products of vectors from V and W.
-
Bilinearity: The tensor product is bilinear, meaning it is linear in each of its arguments. This means that for vectors u₁, u₂ ∈ V and v ∈ W:
(αu₁ + βu₂) ⊗ v = α(u₁ ⊗ v) + β(u₂ ⊗ v)
and similarly for the second argument.
-
Universality: The tensor product is characterized by a universal property, which essentially states that any bilinear map from V x W to another vector space can be uniquely factored through the tensor product V ⊗ W. This property ensures a certain uniqueness and consistency in the construction of the tensor product.
Applications: A Multifaceted Tool
The tensor product is not merely an abstract mathematical concept. It's a powerful tool with applications across diverse fields:
-
Quantum Mechanics: Tensor products are crucial for representing multi-particle quantum systems. The state of a composite system is described by the tensor product of the states of its individual components.
-
Machine Learning: Tensor operations form the backbone of many machine learning algorithms, particularly in deep learning. Tensor networks are used to represent complex relationships in data and model parameters.
-
Computer Graphics and Image Processing: Tensors are used to represent images and transformations in computer graphics. Tensor operations facilitate image manipulation, filtering, and analysis.
-
General Relativity and Physics: Tensor calculus, built upon the foundation of tensor products, is the language of general relativity, providing the mathematical framework for describing gravity and spacetime. Tensors represent physical quantities in a coordinate-independent way.
-
Data Science and Statistics: High-dimensional data is often represented and manipulated using tensors. Tensor decomposition techniques are used for dimensionality reduction and feature extraction.
Frequently Asked Questions (FAQs)
-
Q: What is the difference between a tensor product and matrix multiplication?
- A: While matrix multiplication shares similarities with the tensor product in terms of resulting dimensionality, the tensor product is a more fundamental operation. Matrix multiplication is a specific instance of a tensor contraction (a type of tensor operation). The tensor product combines tensors in a structured way, creating a new, larger tensor, while matrix multiplication involves a summation across one dimension.
-
Q: How do I calculate a tensor product in practice?
- A: The calculation of a tensor product depends on the type and order of the tensors involved. For vectors, it's a systematic multiplication as illustrated earlier. For higher-order tensors, specialized libraries (like NumPy in Python) provide efficient functions to perform these computations. The core principle remains the same – a structured combination of elements from the input tensors.
-
Q: What are some common notations for the tensor product?
- A: Besides "⊗," other notations include "×" (especially when discussing vector spaces) and sometimes just juxtaposition (placing the tensors side-by-side). The specific notation used often depends on the context and the author's preference.
-
Q: Are there limitations to using tensor products?
- A: While immensely powerful, tensor products can lead to very large tensors, especially when dealing with high-dimensional data. Computational complexity can become a significant hurdle, necessitating efficient algorithms and specialized hardware (like GPUs) for practical applications.
Conclusion: A Powerful Tool for Understanding Complexity
The seemingly simple expression "3 x 2 x" opens a window into the fascinating world of tensor products. Beyond basic arithmetic, it represents a powerful mathematical operation with far-reaching implications across many scientific and technological domains. Understanding the tensor product is crucial for anyone venturing into fields involving complex data representations, multi-dimensional systems, and advanced mathematical modeling. While the mathematical underpinnings can be quite intricate, the fundamental idea of a structured combination of tensor elements remains the key to unlocking its potential. From quantum mechanics to machine learning, the tensor product continues to play a pivotal role in our quest to understand and model the complexity of the world around us. Its significance extends far beyond a simple arithmetic calculation, representing instead a cornerstone of modern mathematical and scientific thought.
Latest Posts
Latest Posts
-
Human Geography Features
Sep 12, 2025
-
60 Of 250
Sep 12, 2025
-
120 Of 60
Sep 12, 2025
-
4 X 9
Sep 12, 2025
-
Milliliter To Microliter
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 3x 2 X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.