6 X 13
stanleys
Sep 15, 2025 · 7 min read
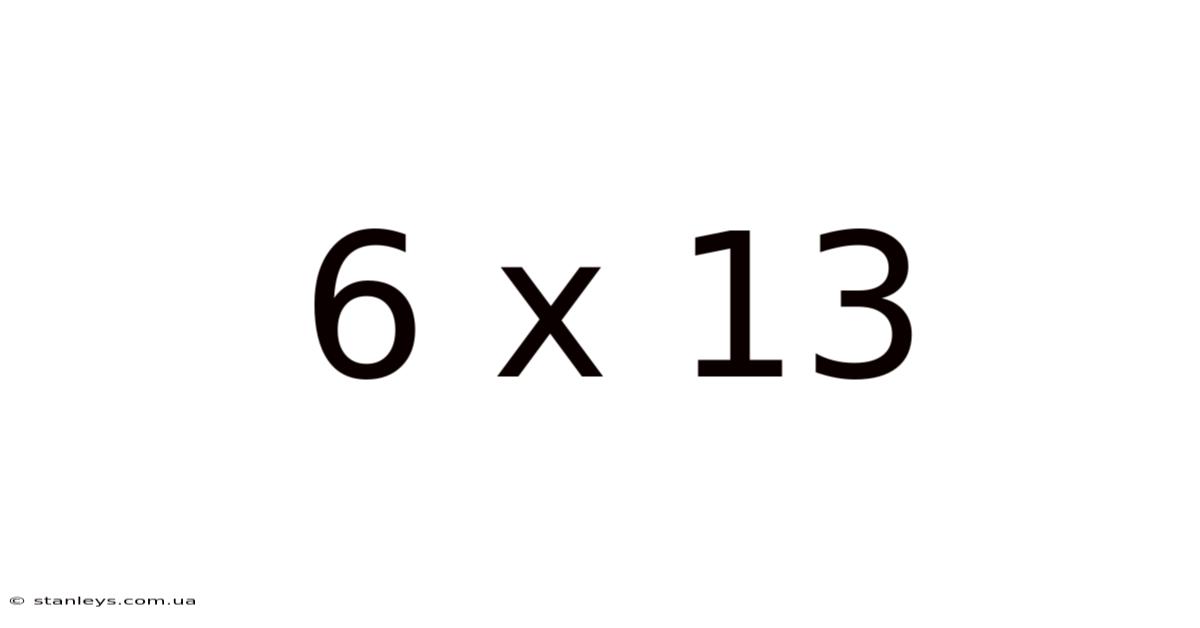
Table of Contents
Unlocking the Mysteries of 6 x 13: A Deep Dive into Multiplication, Factorization, and More
This article explores the seemingly simple multiplication problem of 6 x 13, delving far beyond the immediate answer of 78. We will examine its mathematical properties, explore related concepts such as factorization, prime numbers, and divisibility rules, and even touch upon its practical applications. Understanding this seemingly basic equation provides a strong foundation for more complex mathematical concepts. This exploration is perfect for students wanting to solidify their understanding of multiplication, teachers seeking enriching material, or anyone curious about the hidden depths within a seemingly simple calculation.
I. The Fundamentals: 6 x 13 = 78
At its core, 6 x 13 represents repeated addition: adding six thirteen times, or adding thirteen six times. This fundamental understanding is crucial, especially for younger learners. Visual aids, such as arrays (a rectangular arrangement of objects) or number lines, can be incredibly helpful in solidifying this concept. Imagine arranging 6 rows of 13 objects each; counting them all would yield 78. This simple visualization connects abstract multiplication to concrete reality.
The commutative property of multiplication states that the order of the numbers doesn't affect the product. Therefore, 6 x 13 is equivalent to 13 x 6. This seemingly trivial fact becomes significant when considering different calculation strategies. Multiplying 13 x 6 might be easier for some individuals due to the familiarity with multiplying by 6 (easily achieved through repeated addition of 6).
II. Factorization: Breaking Down 78
Factorization involves expressing a number as a product of its factors. 78 can be factored in several ways:
- 2 x 39: This is a simple factorization, readily apparent given that 78 is an even number (divisible by 2).
- 3 x 26: The divisibility rule for 3 (the sum of the digits must be divisible by 3) shows us 7 + 8 = 15, which is divisible by 3, confirming this factorization.
- 6 x 13: This is the original problem itself, showing that 6 and 13 are factors of 78.
- 2 x 3 x 13: This represents the prime factorization of 78. Prime factorization expresses a number as a product of only prime numbers (numbers divisible only by 1 and themselves). In this case, 2 and 3 are prime, and 13 is also a prime number. Prime factorization is unique to every number and forms the basis for numerous mathematical concepts.
Understanding factorization is crucial for solving many mathematical problems, including simplifying fractions, finding the greatest common divisor (GCD), and the least common multiple (LCM) of numbers. The ability to quickly factor numbers aids in algebraic manipulation and problem-solving skills.
III. Divisibility Rules: Quick Checks for Factors
Divisibility rules offer quick methods to determine if a number is divisible by certain integers without performing the actual division. Let's look at how these rules apply to 78:
- Divisibility by 2: The last digit is 8, which is an even number, so 78 is divisible by 2.
- Divisibility by 3: The sum of the digits (7 + 8 = 15) is divisible by 3, confirming 78's divisibility by 3.
- Divisibility by 6: Since 78 is divisible by both 2 and 3, it's also divisible by 6 (as 6 = 2 x 3).
- Divisibility by 13: This is less intuitive, but 78/13 = 6 confirms this. There isn't a simple divisibility rule for 13.
These rules are not only efficient for checking divisibility but also provide insights into the factors of a number. They are invaluable tools for simplifying calculations and improving mathematical fluency.
IV. Prime Numbers and Their Significance
The prime factorization of 78 (2 x 3 x 13) highlights the importance of prime numbers. Prime numbers are the building blocks of all other integers, and understanding them is foundational to number theory. The prime factorization is unique to each number, and this uniqueness has profound implications in cryptography and other advanced mathematical fields.
The fact that 13 is a prime number within this factorization is noteworthy. Prime numbers are fascinating in their unpredictability, with no easy formula to generate them. Their distribution throughout the number system is an area of ongoing mathematical research.
V. Applications of 6 x 13 in Real-World Scenarios
While seemingly abstract, the concept of 6 x 13, and multiplication in general, has numerous practical applications:
- Counting Objects: Imagine arranging items in a grid, such as arranging 6 rows of 13 chairs in an auditorium.
- Calculating Costs: If an item costs $13, the total cost of 6 such items would be 6 x $13 = $78.
- Measurement Conversions: Many conversion factors involve multiplication. For instance, if you need to convert inches to feet (1 foot = 12 inches) and are working with dimensions involving 13 and 6 (though this is an artificial example to connect to our central topic), understanding multiplication is vital.
- Area Calculation: If a rectangle measures 6 units by 13 units, its area is 78 square units.
These are only a few examples illustrating that multiplication, even seemingly simple problems like 6 x 13, underlies numerous real-world situations. Understanding this connection fosters appreciation for the practical value of mathematical concepts.
VI. Exploring Different Calculation Methods
There are various methods for calculating 6 x 13:
- Standard Multiplication: The traditional method involves multiplying the ones digit (6 x 3 = 18) and tens digit separately (6 x 10 = 60), then adding the results (60 + 18 = 78).
- Distributive Property: This method involves breaking down one factor into simpler terms. For instance, we can think of 13 as (10 + 3), so 6 x 13 = 6 x (10 + 3) = (6 x 10) + (6 x 3) = 60 + 18 = 78.
- Mental Math Techniques: With practice, one can develop mental math skills to quickly calculate 6 x 13. For instance, one could double 13 to get 26, then triple 26 (26 + 26 + 26 = 78).
The choice of method often depends on personal preference and the context of the calculation. Exploring various methods helps to improve flexibility and efficiency in mathematical problem-solving.
VII. Advanced Concepts: Modular Arithmetic and Beyond
While beyond the scope of a purely introductory exploration of 6 x 13, we can briefly touch upon how this simple equation can connect to more advanced mathematical concepts. Consider modular arithmetic: finding the remainder after division by a specific number (the modulus). For example, 78 modulo 5 (written as 78 mod 5) is 3, because 78 divided by 5 leaves a remainder of 3. This seemingly simple concept has far-reaching implications in cryptography and computer science.
Similarly, the concepts of greatest common divisor (GCD) and least common multiple (LCM) are deeply linked to factorization, which we explored earlier in relation to 78. Understanding the factors of 78 is directly relevant to calculating its GCD and LCM with other numbers.
VIII. Frequently Asked Questions (FAQ)
Q: What is the simplest way to calculate 6 x 13?
A: The simplest method depends on individual preference. The standard multiplication algorithm, the distributive property, or mental math techniques can all be efficient.
Q: Why is the prime factorization of 78 important?
A: The prime factorization (2 x 3 x 13) is unique to 78 and is fundamental to many higher-level mathematical concepts, including number theory and cryptography.
Q: Are there any real-world applications of this multiplication problem?
A: Yes, numerous applications exist, including counting objects, calculating costs, area calculations, and various conversion factors in measurement.
Q: How can I improve my multiplication skills?
A: Practice is key. Use various methods, including memorization, using visual aids, and applying multiplication in real-world problems.
IX. Conclusion: The Richness of a Simple Equation
This exploration of 6 x 13 demonstrates that even the simplest mathematical problems can reveal a surprising depth of mathematical principles and applications. From the fundamental concept of repeated addition to the more advanced concepts of prime factorization, divisibility rules, and modular arithmetic, this seemingly basic equation serves as a springboard for understanding much broader mathematical concepts. By appreciating the interconnectedness of mathematical ideas, we can foster a deeper understanding and appreciation for the beauty and utility of mathematics. Remember that the journey of mathematical learning is a continuous one, filled with opportunities for discovery and growth, starting with the seemingly simple 6 x 13.
Latest Posts
Latest Posts
-
X 3 5
Sep 15, 2025
-
75 Of 65
Sep 15, 2025
-
20 Of 275
Sep 15, 2025
-
68f To Celsius
Sep 15, 2025
-
1000 X 12
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 6 X 13 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.