5 6 12
stanleys
Sep 13, 2025 · 6 min read
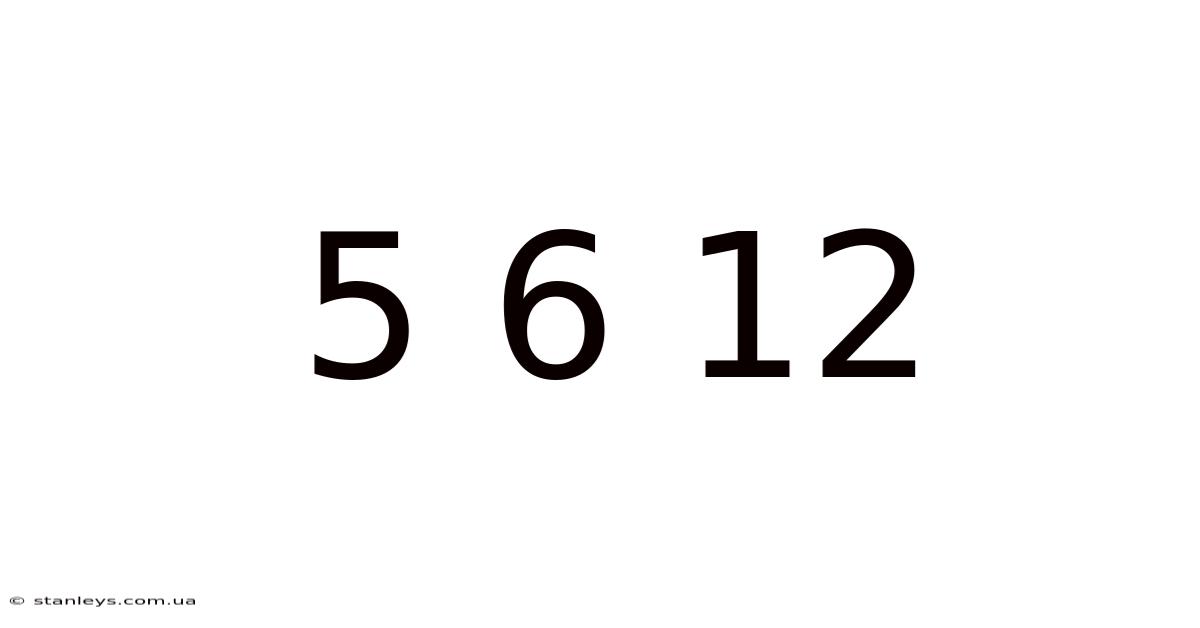
Table of Contents
Decoding the Mysterious Sequence: 5, 6, 12 – Exploring Mathematical Relationships and Patterns
The seemingly simple sequence 5, 6, 12 might appear unremarkable at first glance. However, a deeper dive reveals a fascinating world of mathematical relationships and potential patterns, opening doors to exploring various mathematical concepts. This article will explore several interpretations of this sequence, delving into the possibilities behind its seemingly arbitrary arrangement and uncovering the underlying mathematical principles. We'll examine different approaches to understanding this sequence, from simple arithmetic to more complex mathematical structures. This exploration will provide a comprehensive understanding of the diverse ways we can interpret and analyze numerical sequences.
I. Introduction: The Allure of Number Sequences
Number sequences, like 5, 6, 12, have captivated mathematicians and puzzle enthusiasts for centuries. These sequences often hide intricate patterns and relationships, challenging us to decipher the underlying rules governing their progression. The beauty lies not just in finding a solution but also in the process of exploration, requiring creativity, logical reasoning, and a deep understanding of mathematical principles. The sequence 5, 6, 12, despite its brevity, offers a prime example of this intellectual pursuit. We will explore different perspectives, considering potential interpretations and justifying their mathematical validity.
II. Exploring Arithmetic Progressions and Geometric Progressions
One common approach to analyzing numerical sequences involves exploring arithmetic progressions and geometric progressions.
A. Arithmetic Progressions: An arithmetic progression is a sequence where the difference between consecutive terms remains constant. Let's examine if our sequence 5, 6, 12 fits this model. The difference between 5 and 6 is 1, while the difference between 6 and 12 is 6. Since the difference isn't constant, the sequence does not represent a simple arithmetic progression.
B. Geometric Progressions: A geometric progression is a sequence where the ratio between consecutive terms remains constant. Again, let's check our sequence. The ratio between 5 and 6 is 6/5 (approximately 1.2), and the ratio between 6 and 12 is 2. The ratio is not constant, so this sequence does not represent a simple geometric progression either.
III. Delving into More Complex Relationships: Potential Interpretations
Since simple arithmetic and geometric progressions fail, we need to consider more intricate relationships. Several interpretations are possible, each with its own mathematical justification.
A. Combination of Operations: One approach involves examining combinations of arithmetic and other mathematical operations. For example, one might postulate the following:
- Start with 5.
- Add 1 to get 6.
- Multiply by 2 to get 12.
While this works for the given sequence, it doesn't necessarily define a recursive rule for generating further terms. This interpretation is valid but limited in its predictive power for extending the sequence.
B. Modular Arithmetic and Cyclic Patterns: Another approach involves considering modular arithmetic, where numbers "wrap around" after reaching a certain modulus. While not immediately apparent, exploring different moduli might reveal hidden cyclic patterns. However, without further terms in the sequence, definitively establishing a modular pattern remains speculative.
C. Prime Factorization and Number Theory: Analyzing the prime factorization of each number in the sequence can be insightful.
- 5 is a prime number.
- 6 = 2 x 3
- 12 = 2 x 2 x 3
Notice the presence of the prime factors 2 and 3. One might speculate on a pattern related to the combination or manipulation of these prime factors, but without more data, this interpretation remains conjecture.
IV. Introducing Fibonacci-Like Sequences and Recursive Relationships
While not a classic Fibonacci sequence (where each term is the sum of the two preceding terms), we could explore if a similar recursive relationship exists. Let's consider some possibilities:
-
Modified Fibonacci: We could investigate sequences where the next term is a function of the previous terms, not necessarily a simple sum. However, without more terms, it's impossible to definitively establish a recursive rule.
-
Recursive Relationship with Operations: It's plausible that a recursive rule might involve not only addition but also other operations, such as multiplication or exponentiation. Developing such a rule requires further terms in the sequence.
V. Exploring Polynomial Relationships and Curve Fitting
Another approach involves fitting a polynomial curve to the data points. Since we only have three data points (5, 6, 12), we can easily find a polynomial (at most a quadratic) that passes through these points. However, this polynomial wouldn't necessarily predict future terms accurately. The ability to extrapolate relies heavily on the underlying pattern. If the pattern is indeed polynomial, the predictive power would be higher. If not, it will only be a curve fitting the given three points.
VI. The Importance of Context and Further Data
The key takeaway from this analysis is the crucial role of context and the need for more data. The sequence 5, 6, 12, in its current form, allows for multiple interpretations, none of which can be definitively proven without further terms. The ambiguity highlights the importance of providing sufficient data when dealing with mathematical sequences. Additional terms would significantly constrain the possibilities and potentially reveal a clear pattern.
VII. Mathematical Modeling and Prediction
If we were to receive additional terms in the sequence, we could employ more sophisticated mathematical modeling techniques, including:
-
Time Series Analysis: If the sequence represents data over time, time series analysis could reveal underlying trends and seasonality.
-
Regression Analysis: This statistical method could help identify the best-fitting model, revealing the relationship between the sequence position and the value.
-
Machine Learning: Advanced machine learning algorithms could identify complex patterns and predict future terms even with noisy or incomplete data.
VIII. Conclusion: The Ongoing Search for Pattern and Meaning
The exploration of the sequence 5, 6, 12 highlights the fascinating interplay between observation, hypothesis formation, and mathematical rigor. While we've explored several interpretations, the lack of further terms prevents us from conclusively determining the underlying rule. This ambiguity underscores the crucial role of data in mathematical analysis and the ever-present challenge of uncovering hidden patterns in seemingly random sequences. The journey of exploring this sequence exemplifies the creative and analytical thinking inherent in mathematical problem-solving. Further data is the key to unlocking the secrets held within this seemingly simple sequence.
IX. Frequently Asked Questions (FAQ)
Q1: Is there a single correct answer to this sequence?
A1: Without more data points, there is no single definitively correct answer. Several plausible interpretations exist, each with its own mathematical justification.
Q2: How can I find more sequences like this to practice?
A2: Online resources and mathematical puzzle books offer a wealth of number sequences for practice. Search for "number sequence puzzles" or "mathematical sequences" to find various examples.
Q3: What mathematical skills are needed to analyze number sequences?
A3: A strong foundation in arithmetic, algebra, and an understanding of various sequence types (arithmetic, geometric, Fibonacci, etc.) are beneficial. Statistical knowledge and familiarity with curve fitting are also valuable for more complex analyses.
Q4: Can computer programs help analyze number sequences?
A4: Yes, computer programs can automate the process of finding patterns and fitting curves to data. Programming languages like Python, with libraries like NumPy and SciPy, are particularly well-suited for this task.
Q5: What if the sequence is completely random?
A5: If the sequence is truly random, no underlying pattern exists. Statistical tests could be used to determine the likelihood of randomness.
This exploration of the sequence 5, 6, 12 provides a glimpse into the world of mathematical problem-solving and pattern recognition. While a definitive answer remains elusive without further information, the journey of exploration reveals the rich tapestry of mathematical concepts and techniques that can be applied to unravel the mysteries within numerical sequences. The process itself highlights the power of critical thinking, creativity, and the importance of rigorous mathematical reasoning.
Latest Posts
Latest Posts
-
80 Of 150
Sep 13, 2025
-
Rpm In Rad Sec
Sep 13, 2025
-
450ml In Ounces
Sep 13, 2025
-
Factor For 42
Sep 13, 2025
-
Antonyms For Respite
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 5 6 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.