80 Of 150
stanleys
Sep 13, 2025 · 5 min read
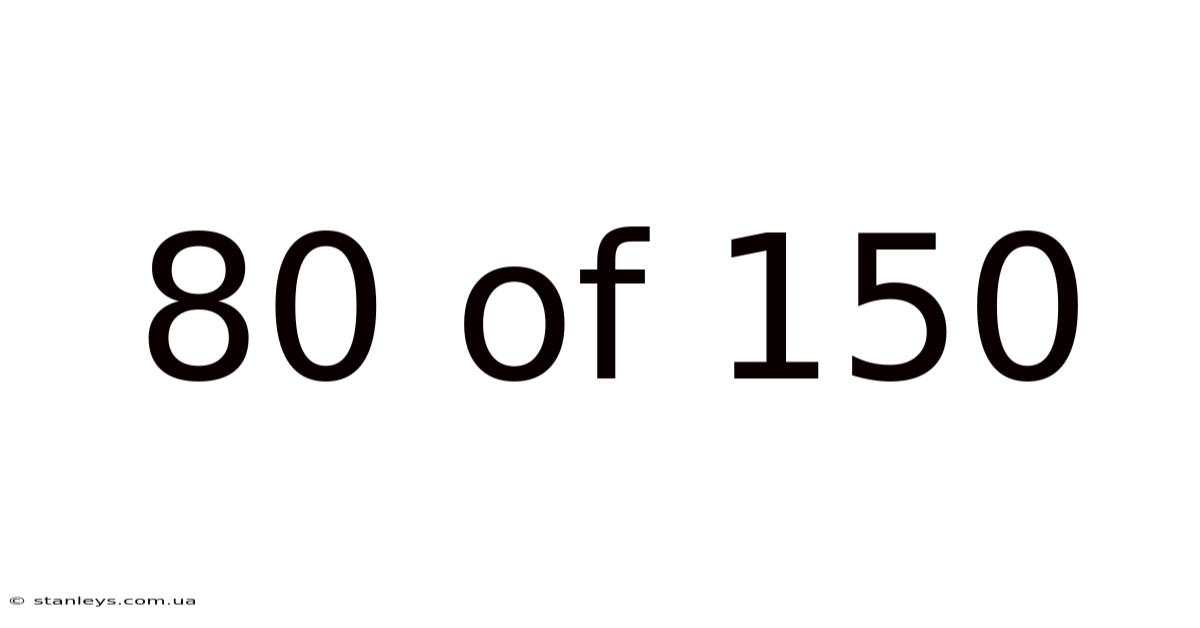
Table of Contents
Understanding and Mastering the Fraction 80/150: A Comprehensive Guide
Introduction:
The fraction 80/150, while seemingly simple, presents a valuable opportunity to explore fundamental concepts in mathematics. This article will delve into a comprehensive understanding of this fraction, covering its simplification, decimal and percentage equivalents, real-world applications, and related mathematical concepts. Whether you're a student struggling with fractions, a teacher looking for supplementary material, or simply someone curious about mathematics, this guide will equip you with the knowledge and skills to confidently tackle 80/150 and similar fractions. We will explore various methods for simplification, demonstrate the conversion process to decimals and percentages, and provide practical examples illustrating the relevance of understanding fractions in everyday life.
Simplifying 80/150: Finding the Greatest Common Divisor (GCD)
The first step in working with any fraction is to simplify it to its lowest terms. This involves finding the greatest common divisor (GCD) of the numerator (80) and the denominator (150). The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder.
There are several methods to find the GCD:
-
Listing Factors: We can list the factors of both 80 and 150 and identify the largest common factor.
Factors of 80: 1, 2, 4, 5, 8, 10, 16, 20, 40, 80 Factors of 150: 1, 2, 3, 5, 6, 10, 15, 25, 30, 50, 75, 150
The largest common factor is 10.
-
Prime Factorization: This method involves breaking down both numbers into their prime factors.
80 = 2 x 2 x 2 x 2 x 5 = 2⁴ x 5 150 = 2 x 3 x 5 x 5 = 2 x 3 x 5²
The common prime factors are 2 and 5. The GCD is the product of the lowest powers of the common prime factors: 2¹ x 5¹ = 10
-
Euclidean Algorithm: This is a more efficient method for larger numbers. It involves repeatedly applying the division algorithm until the remainder is 0. The last non-zero remainder is the GCD.
150 = 10 x 15 + 0
The remainder is 0, indicating that 10 is the GCD.
Now that we've found the GCD (10), we can simplify the fraction:
80/150 = (80 ÷ 10) / (150 ÷ 10) = 8/15
Therefore, the simplified form of 80/150 is 8/15.
Converting 80/150 to a Decimal
To convert a fraction to a decimal, we divide the numerator by the denominator. Using the simplified fraction 8/15:
8 ÷ 15 ≈ 0.5333...
The decimal representation of 8/15 is approximately 0.5333, which is a recurring decimal. The three repeats infinitely.
Converting 80/150 to a Percentage
To convert a fraction to a percentage, we multiply the decimal equivalent by 100:
0.5333... x 100 ≈ 53.33%
Therefore, 80/150 is approximately 53.33%.
Real-World Applications of 80/150
Understanding fractions like 80/150 is crucial in various real-world scenarios:
-
Calculating Percentages: If a student answered 80 questions correctly out of a total of 150, their score would be 53.33%. This is fundamental in assessing academic performance.
-
Proportion and Ratio: Imagine a recipe that calls for 150 grams of flour and 80 grams of sugar. The ratio of sugar to flour would be 80:150, which simplifies to 8:15. This is essential in cooking and baking.
-
Data Analysis: In statistics, fractions represent proportions within a dataset. For example, if 80 out of 150 respondents answered "yes" to a survey question, this fraction helps analyze the data and draw conclusions.
Further Exploration: Understanding Fractions More Deeply
This section expands on the fundamental concepts related to fractions, building upon the knowledge gained from working with 80/150.
Types of Fractions:
- Proper Fractions: The numerator is smaller than the denominator (e.g., 8/15).
- Improper Fractions: The numerator is larger than or equal to the denominator (e.g., 150/80).
- Mixed Numbers: A combination of a whole number and a proper fraction (e.g., 1 and 70/80, which simplifies to 1 and 7/8).
Operations with Fractions:
- Addition and Subtraction: To add or subtract fractions, they must have a common denominator.
- Multiplication: Multiply the numerators together and the denominators together.
- Division: Invert the second fraction and multiply.
Equivalent Fractions:
Equivalent fractions represent the same value. For example, 80/150, 8/15, 16/30, and 40/75 are all equivalent fractions.
Fraction to Decimal Conversion:
As demonstrated earlier, converting a fraction to a decimal involves dividing the numerator by the denominator. Understanding recurring decimals (like in the case of 8/15) is crucial.
Decimal to Fraction Conversion:
Converting a decimal to a fraction involves expressing the decimal as a fraction with a power of 10 as the denominator and then simplifying it. For example, 0.75 is equal to 75/100 which can be simplified to 3/4.
Percentage to Fraction Conversion:
A percentage can be converted into a fraction by placing it over 100 and then simplifying. For instance, 60% is equal to 60/100, which simplifies to 3/5.
Frequently Asked Questions (FAQ)
Q1: What is the simplest form of 80/150?
A1: The simplest form of 80/150 is 8/15.
Q2: How do I convert 80/150 to a decimal?
A2: Divide 80 by 150. The result is approximately 0.5333 (a recurring decimal).
Q3: How do I convert 80/150 to a percentage?
A3: Multiply the decimal equivalent (approximately 0.5333) by 100. The result is approximately 53.33%.
Q4: Are there any other equivalent fractions to 80/150?
A4: Yes, many. For example, 16/30, 40/75, 32/60 etc.
Q5: Why is simplifying fractions important?
A5: Simplifying fractions makes them easier to work with and understand. It also provides a clearer representation of the value.
Conclusion
Understanding the fraction 80/150 goes beyond simply knowing its simplified form or decimal equivalent. It provides a foundation for grasping more complex mathematical concepts, and highlights the practical applications of fractions in numerous real-world contexts. By mastering the skills of simplifying, converting between fractions, decimals, and percentages, and understanding the underlying mathematical principles, individuals can confidently approach similar fractional problems and apply this knowledge effectively in various aspects of life. Remember that consistent practice and a curious approach to mathematics are key to building a strong understanding of these important concepts. This guide serves as a comprehensive starting point; further exploration and practice will solidify your understanding and build your confidence in working with fractions.
Latest Posts
Latest Posts
-
127lbs In Kg
Sep 13, 2025
-
175 To Kg
Sep 13, 2025
-
6 7kg In Lbs
Sep 13, 2025
-
75 Of 400
Sep 13, 2025
-
5 5cm To Mm
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 80 Of 150 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.