Rpm In Rad/sec
stanleys
Sep 13, 2025 · 5 min read
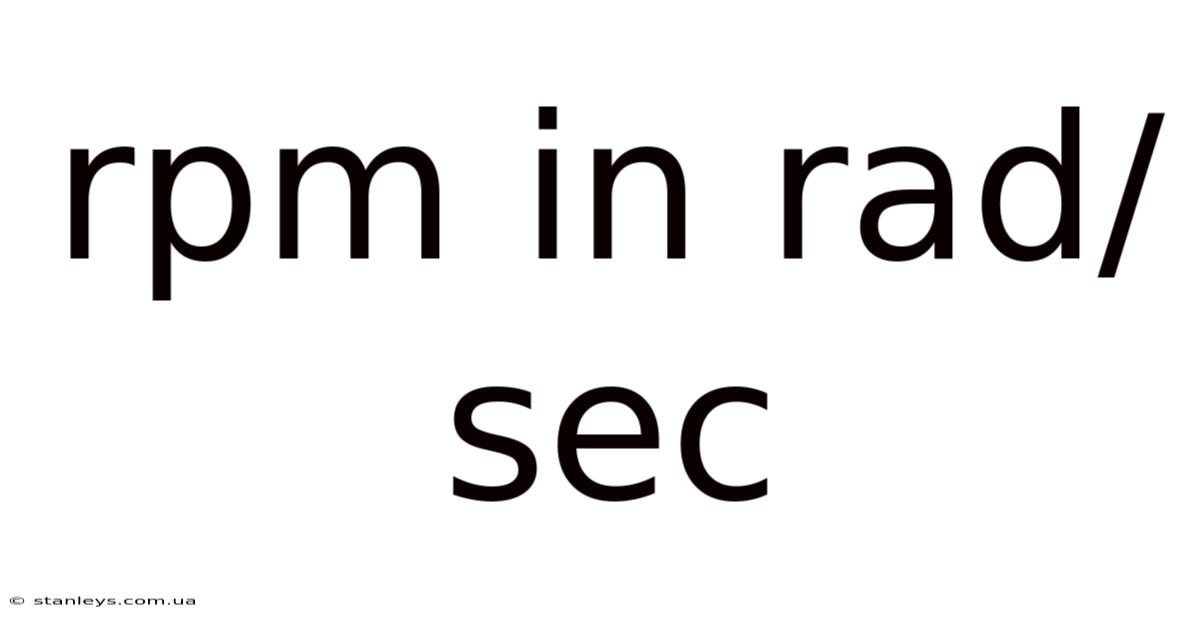
Table of Contents
Understanding RPM and its Conversion to rad/sec: A Comprehensive Guide
Rotational speed, a crucial concept in various fields like engineering, physics, and automotive mechanics, is often expressed in revolutions per minute (RPM). However, for many scientific and engineering calculations, it's more convenient to use radians per second (rad/sec). This article provides a comprehensive understanding of RPM, its significance, and how to effectively convert it to rad/sec, covering the underlying principles and practical applications. This guide will delve into the mathematical relationships, provide step-by-step conversion examples, and address frequently asked questions to ensure a thorough grasp of this essential concept.
What is RPM?
RPM, or revolutions per minute, is a unit of measurement that describes the number of complete rotations an object makes around a fixed axis in one minute. It's a widely used measure for rotational speed, especially in contexts involving machinery like engines, motors, turbines, and rotating equipment. A higher RPM indicates a faster rotational speed. For example, an engine running at 2000 RPM completes 2000 full rotations in a single minute.
What are Radians and rad/sec?
Radians are a unit of angular measurement. Unlike degrees, where a full circle is 360 degrees, a radian is defined by the ratio of the arc length to the radius of a circle. One radian is the angle subtended at the center of a circle by an arc equal in length to the radius. Therefore, a full circle encompasses 2π radians (approximately 6.28 radians).
Radians per second (rad/sec), also denoted as rad/s, is the unit of angular velocity. It represents the rate of change of angular displacement (measured in radians) with respect to time (measured in seconds). A higher rad/sec value indicates a faster angular velocity. Essentially, it tells us how many radians an object rotates through each second.
Why Convert RPM to rad/sec?
While RPM is readily understandable and widely used in practical applications, it's often less suitable for complex calculations involving angular velocity, angular acceleration, and other rotational dynamics. The radian is the SI unit for angular measurement, making rad/sec the preferred unit in scientific and engineering calculations. Using rad/sec simplifies equations and leads to consistent units throughout the calculations, preventing potential errors. Many physics formulas, particularly those involving rotational motion and torque calculations, require angular velocity to be expressed in rad/sec.
The Conversion Formula: From RPM to rad/sec
The conversion from RPM to rad/sec is relatively straightforward. We leverage the relationship between revolutions, radians, and time:
- 1 revolution = 2π radians
- 1 minute = 60 seconds
Therefore, the conversion formula is:
ω (rad/sec) = (RPM * 2π) / 60
Where:
- ω represents angular velocity in rad/sec
- RPM represents rotational speed in revolutions per minute
- π (pi) ≈ 3.14159
Step-by-Step Conversion Examples
Let's work through some examples to solidify our understanding:
Example 1: Convert 1500 RPM to rad/sec.
- Substitute the value of RPM into the formula: ω = (1500 * 2π) / 60
- Calculate: ω ≈ (1500 * 6.28318) / 60 ≈ 157.08 rad/sec
Therefore, 1500 RPM is equivalent to approximately 157.08 rad/sec.
Example 2: A motor spins at 3000 RPM. What's its angular velocity in rad/sec?
- Substitute: ω = (3000 * 2π) / 60
- Calculate: ω ≈ (3000 * 6.28318) / 60 ≈ 314.16 rad/sec
The motor's angular velocity is approximately 314.16 rad/sec.
Example 3: Convert 60 RPM to rad/sec.
- Substitute: ω = (60 * 2π) / 60
- Calculate: ω ≈ 6.28318 rad/sec
This example simplifies to just 2π rad/sec, highlighting the direct relationship between one revolution and 2π radians.
Applications of RPM to rad/sec Conversion
The conversion from RPM to rad/sec finds applications in numerous fields:
- Robotics: Calculating the angular velocities of robotic joints for precise movement control.
- Automotive Engineering: Determining the angular velocity of engine components, wheels, and transmissions for performance analysis and design.
- Aerospace Engineering: Analyzing the rotational speeds of turbines, propellers, and gyroscopes.
- Power Generation: Calculating the rotational speed of generators and turbines in power plants.
- Industrial Machinery: Determining the speed of various rotating parts in manufacturing processes.
- Physics and Engineering Calculations: Solving problems involving rotational motion, torque, angular momentum, and kinetic energy.
Understanding Angular Velocity and its Significance
Angular velocity (ω), measured in rad/sec, represents how fast an object is rotating. It's a vector quantity, meaning it has both magnitude (speed of rotation) and direction (axis of rotation). Understanding angular velocity is crucial in:
- Calculating Centripetal Force: The force that keeps an object moving in a circular path.
- Determining Angular Momentum: A measure of an object's rotational inertia.
- Analyzing Rotational Kinetic Energy: The energy an object possesses due to its rotation.
- Predicting Rotational Motion: Using equations of motion to predict the future position and velocity of rotating objects.
Frequently Asked Questions (FAQ)
Q1: Can I convert from rad/sec back to RPM?
Yes, simply rearrange the formula: RPM = (ω * 60) / 2π
Q2: What if I have rotational speed in revolutions per second (rev/sec)?
To convert rev/sec to rad/sec, simply multiply by 2π: ω (rad/sec) = rev/sec * 2π
Q3: Are there other units for angular velocity besides rad/sec and RPM?
Yes, other units include degrees per second (°/sec) and revolutions per second (rev/s). However, rad/sec is preferred for its compatibility with SI units and ease of use in calculations.
Q4: Why is the radian a dimensionless quantity?
A radian is defined as the ratio of arc length to radius, both of which have the same units (e.g., meters). Therefore, the units cancel out, making the radian dimensionless.
Q5: What about negative angular velocity?
A negative angular velocity simply indicates the direction of rotation. For example, counter-clockwise rotation might be defined as positive, while clockwise rotation is negative. The convention is usually specified in the context of the problem.
Conclusion
Understanding the relationship between RPM and rad/sec is fundamental for anyone working with rotating systems. While RPM provides a readily understandable measure of rotational speed, the conversion to rad/sec is essential for many calculations in science and engineering. By applying the simple conversion formula and understanding the underlying principles, one can seamlessly transition between these units and accurately solve problems related to rotational motion and dynamics. Mastering this conversion enhances your ability to analyze and design systems involving rotating components across various disciplines. Remember to always pay attention to the units used and consistently apply the conversion formula to ensure accuracy in your calculations.
Latest Posts
Latest Posts
-
127lbs In Kg
Sep 13, 2025
-
175 To Kg
Sep 13, 2025
-
6 7kg In Lbs
Sep 13, 2025
-
75 Of 400
Sep 13, 2025
-
5 5cm To Mm
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Rpm In Rad/sec . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.