5 2x 1
stanleys
Sep 16, 2025 · 6 min read
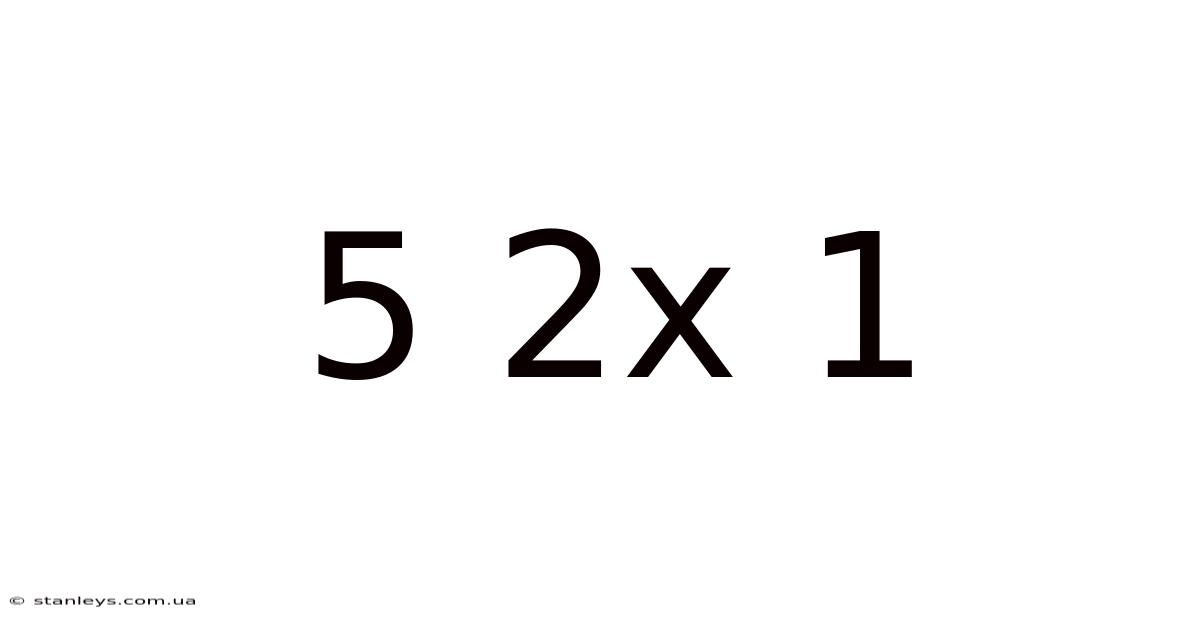
Table of Contents
Decoding 5 x 2 x 1: A Deep Dive into Factorials, Permutations, and Combinations
This article explores the seemingly simple mathematical expression "5 x 2 x 1," revealing its deep connections to factorials, permutations, and combinations. Understanding this seemingly simple equation unlocks a powerful tool for solving complex probability and arrangement problems in mathematics, statistics, and even computer science. We'll break down the concept step-by-step, providing clear explanations and examples to solidify your understanding.
Introduction: Unveiling the Power of Factorials
At first glance, 5 x 2 x 1 might seem like a straightforward multiplication problem, resulting in 10. However, this expression represents a fundamental concept in mathematics: the factorial. The factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n. In our case, 5 x 2 x 1 is equivalent to 5!, read as "5 factorial."
Therefore, 5! = 5 x 4 x 3 x 2 x 1 = 120. The seemingly insignificant calculation of 5 x 2 x 1 is actually a part of a larger calculation, illustrating the core principle of factorials. Understanding factorials opens the door to understanding more complex mathematical concepts like permutations and combinations.
Understanding Permutations: Arranging Objects in Order
Permutations deal with the number of ways to arrange a set of objects in a specific order. Consider you have five distinct books (A, B, C, D, E) and you want to arrange them on a shelf. How many different ways can you do this? This is a permutation problem.
The first position on the shelf can be filled with any of the five books. Once the first position is filled, there are only four books left to choose from for the second position. Then three for the third, two for the fourth, and finally, only one book left for the last position. Therefore, the total number of ways to arrange the five books is: 5 x 4 x 3 x 2 x 1 = 120. This is precisely 5!.
The general formula for permutations of n distinct objects taken r at a time is given by:
P(n, r) = n! / (n - r)!
In our book example, n = 5 (total number of books) and r = 5 (we're using all the books). So, P(5, 5) = 5! / (5 - 5)! = 5! / 0! = 120 (remember that 0! = 1).
Let's consider a slightly different scenario. Suppose we only want to arrange three of the five books. Then n = 5 and r = 3. The calculation becomes:
P(5, 3) = 5! / (5 - 3)! = 5! / 2! = (5 x 4 x 3 x 2 x 1) / (2 x 1) = 60
This means there are 60 different ways to arrange three of the five books on the shelf. Notice how 5 x 2 x 1 (part of 5!) is still implicitly involved in the calculation.
Exploring Combinations: Selecting Objects Without Order
Combinations, unlike permutations, are concerned with selecting a subset of objects from a larger set, where the order of selection doesn't matter. Let's use the same five books example.
Suppose you want to choose three books to read, but the order in which you choose them doesn't matter. This is a combination problem. The formula for combinations of n objects taken r at a time is:
C(n, r) = n! / (r! * (n - r)!)
For choosing three books from five, n = 5 and r = 3:
C(5, 3) = 5! / (3! * (5 - 3)!) = 5! / (3! * 2!) = (5 x 4 x 3 x 2 x 1) / ((3 x 2 x 1) * (2 x 1)) = 10
This means there are 10 different ways to choose three books from five, regardless of the order. Observe that while factorials are crucial to the calculation, the resulting number is significantly smaller than the number of permutations, highlighting the difference between order-dependent (permutations) and order-independent (combinations) selection.
The Scientific Explanation: Probability and Discrete Mathematics
The expression 5 x 2 x 1, and its extension to n!, forms the bedrock of many concepts in probability and discrete mathematics. Factorials arise naturally when calculating the number of possible arrangements or selections. This fundamental principle has far-reaching consequences:
-
Probability Calculations: In probability theory, factorials are essential for calculating probabilities involving permutations and combinations. For example, calculating the probability of drawing specific cards from a deck involves factorials.
-
Counting Techniques: Factorials are crucial in various counting techniques, providing a systematic way to determine the number of possibilities in situations with many choices.
-
Binomial Theorem: The binomial theorem, which describes the expansion of (a + b)^n, relies heavily on combinations and, consequently, factorials.
-
Statistical Inference: Factorials play a role in statistical inference, particularly in hypothesis testing and confidence interval calculations.
-
Algorithm Analysis: In computer science, the analysis of algorithms often involves factorial expressions to represent computational complexity, especially in algorithms dealing with sorting or searching.
Frequently Asked Questions (FAQ)
Q: What if I have to calculate the factorial of a large number? Will it be computationally expensive?
A: Yes, calculating factorials of large numbers can be computationally expensive because the numbers grow extremely rapidly. For large n, specialized algorithms and approximations are often used to avoid computational overflow and improve efficiency.
Q: Are there any other ways to represent or approximate factorials besides direct multiplication?
A: Yes, Stirling's approximation provides a way to approximate large factorials using the exponential function and other mathematical constants, making calculation significantly faster for large numbers.
Q: What's the difference between a permutation and a combination?
A: The key difference lies in whether the order matters. Permutations consider the order of selection, while combinations do not. For example, choosing three books to read in a specific order is a permutation; choosing three books without regard to the reading order is a combination.
Q: What is 0!?
A: 0! is defined as 1. This is a convention established to maintain consistency in mathematical formulas involving factorials.
Q: Can factorials be used for non-integer values?
A: The traditional factorial function is defined only for non-negative integers. However, the concept of factorials can be extended to non-integer values using the Gamma function, a more general function in complex analysis.
Conclusion: From Simple Multiplication to Powerful Concepts
The seemingly simple expression "5 x 2 x 1" serves as a gateway to understanding the profound concepts of factorials, permutations, and combinations. These concepts are not merely abstract mathematical ideas; they are powerful tools used across diverse fields to solve problems involving arrangement, selection, and probability. By grasping the fundamentals of factorials and their applications, you gain a valuable skill set that extends far beyond the initial multiplication problem. The journey from a simple equation to a deeper understanding of mathematical principles highlights the beauty and interconnectedness of mathematics. Mastering these concepts unlocks a universe of possibilities, empowering you to tackle complex problems with confidence and clarity. Further exploration into the applications of factorials and related topics will undoubtedly reveal their even broader importance in mathematics and other quantitative fields.
Latest Posts
Latest Posts
-
Structure In Ozymandias
Sep 16, 2025
-
500g To Oz
Sep 16, 2025
-
Nyc Lat Lon
Sep 16, 2025
-
4x X 2
Sep 16, 2025
-
3x X 2
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 5 2x 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.