3x X 2
stanleys
Sep 16, 2025 · 6 min read
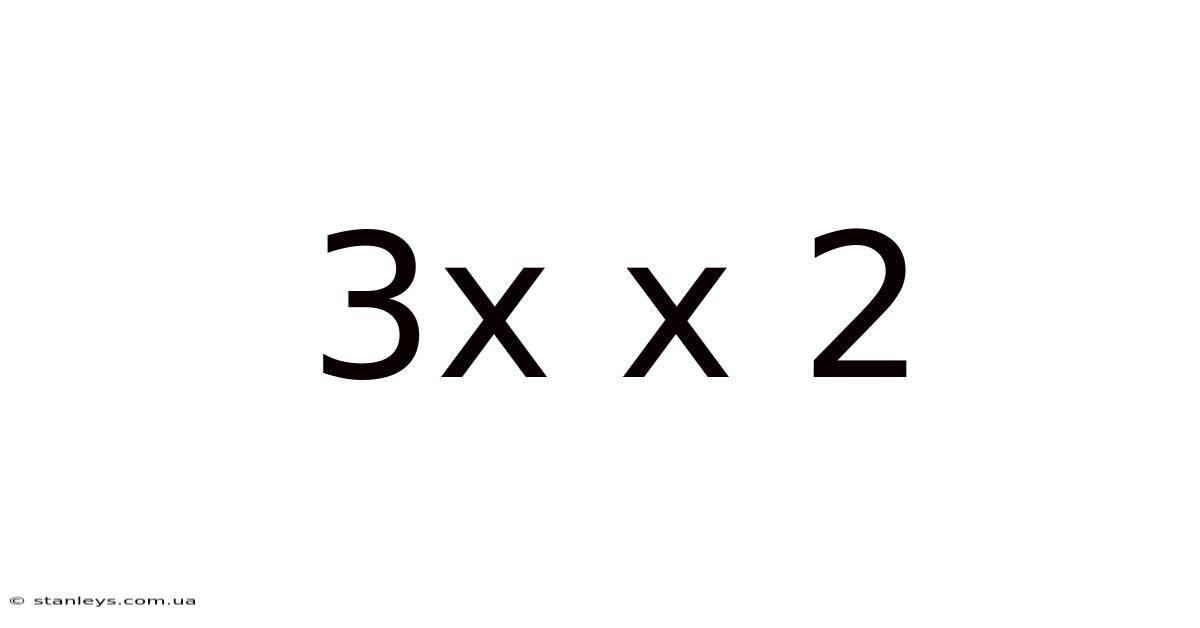
Table of Contents
Decoding 3 x 2: Exploring Multiplication, its Applications, and Extensions
This article delves into the seemingly simple equation "3 x 2," exploring its foundational role in mathematics, its practical applications in everyday life, and its extensions into more complex mathematical concepts. Understanding this fundamental operation is crucial for building a strong mathematical foundation, regardless of your age or background. We will move beyond simply stating the answer (6) and delve into the why and how behind this calculation.
Introduction: The Building Blocks of Multiplication
Multiplication, at its core, represents repeated addition. The expression "3 x 2" can be interpreted as "3 added to itself 2 times," or "2 added to itself 3 times." This seemingly simple concept forms the cornerstone of arithmetic and is fundamental to understanding more advanced mathematical operations like algebra, calculus, and beyond. While seemingly trivial at first glance, mastering this fundamental concept unlocks the door to a vast world of mathematical possibilities. This article aims to illuminate the intricacies of this seemingly simple equation, exploring its practical applications and theoretical underpinnings.
Understanding 3 x 2: Visual and Numerical Representations
Let's visualize "3 x 2" in a few different ways:
-
Repeated Addition: 3 + 3 = 6 or 2 + 2 + 2 = 6. This is the most straightforward way to understand multiplication, especially for beginners.
-
Arrays: Imagine arranging objects in a grid. Three rows with two objects in each row would give you a total of six objects. This visual representation helps to solidify the concept of multiplication as a way to count groups of items.
-
Number Line: Starting at zero, jump forward by two, three times. You'll land on six. This method links multiplication to the visual concept of movement along a number line.
-
Area Model: Imagine a rectangle with a length of 3 units and a width of 2 units. The area of this rectangle would be 3 x 2 = 6 square units. This method connects multiplication to geometry and the concept of area.
The Commutative Property: Order Doesn't Matter (in this case!)
A key property of multiplication is its commutative nature. This means that the order of the numbers doesn't affect the result. 3 x 2 is the same as 2 x 3. Both calculations yield the same answer: 6. This seemingly simple observation is a powerful tool, especially when dealing with larger numbers. It allows for flexibility in how we approach multiplication problems.
Extending the Concept: Beyond 3 x 2
While 3 x 2 is a simple equation, understanding its underlying principles allows us to tackle more complex calculations. Let's consider some extensions:
-
Multiplication with Larger Numbers: The same principles apply when multiplying larger numbers. For example, 15 x 4 can be visualized as fifteen groups of four objects each, or four groups of fifteen. The repeated addition method becomes less practical here, highlighting the power and efficiency of understanding the multiplicative concept itself.
-
Multiplication with Fractions and Decimals: The concept of multiplication extends to fractions and decimals. For example, 3 x 0.5 (or 3 x ½) represents three halves, which equals 1.5. This demonstrates the versatility of multiplication in dealing with different number types.
-
Algebraic Expressions: Multiplication is fundamental to algebraic expressions. The expression 3x represents 3 multiplied by an unknown quantity, x. Understanding multiplication's fundamental principles lays the groundwork for solving algebraic equations and understanding variables.
Real-World Applications of Multiplication: From Everyday Life to Advanced Science
Multiplication is not just a mathematical concept confined to textbooks. It's an integral part of our daily lives:
-
Shopping: Calculating the total cost of multiple items (e.g., buying three apples at $2 each).
-
Cooking: Following recipes that require multiplying ingredient quantities (e.g., doubling a recipe).
-
Construction: Calculating the area or volume of materials needed for a project.
-
Finance: Calculating interest earned on savings or payments on loans.
-
Computer Science: In programming, multiplication is used extensively for calculations, loops, and array manipulation.
-
Physics and Engineering: Many scientific and engineering calculations depend heavily on multiplication, from calculating forces and velocities to modeling complex systems.
Addressing Common Misconceptions About Multiplication
Despite its fundamental nature, some misconceptions can arise regarding multiplication:
-
Multiplication as Always Making Larger: While often true with whole numbers, multiplying by a fraction or decimal less than 1 will actually result in a smaller number (e.g., 3 x 0.5 = 1.5).
-
Confusion with Addition: Students sometimes confuse addition and multiplication, especially in the initial stages of learning. Emphasizing the concept of repeated addition can help clarify this distinction.
-
Difficulty with Larger Numbers: As numbers increase in size, the repeated addition method becomes cumbersome. Understanding the underlying principles of multiplication, such as the distributive property and the use of arrays, aids in handling larger multiplications efficiently.
The Distributive Property: A Powerful Tool for Simplification
The distributive property states that a(b + c) = ab + ac. This property can significantly simplify multiplication problems. For example, let's consider 3 x (2 + 4). Using the distributive property, we can break this down as (3 x 2) + (3 x 4) = 6 + 12 = 18. This method is especially helpful when working with larger numbers or more complex expressions.
Beyond the Basics: Exploring Advanced Concepts
The simple equation 3 x 2 provides a foundation for understanding many advanced mathematical concepts:
-
Exponentiation: Repeated multiplication is the basis of exponentiation (e.g., 3² = 3 x 3 = 9).
-
Matrices: Matrices are rectangular arrays of numbers, and multiplication of matrices is a fundamental operation in linear algebra.
-
Calculus: Derivatives and integrals, central to calculus, involve intricate calculations that build upon the foundation of multiplication.
Frequently Asked Questions (FAQ)
-
What is the inverse operation of multiplication? Division is the inverse operation of multiplication. If 3 x 2 = 6, then 6 / 2 = 3 and 6 / 3 = 2.
-
How can I improve my multiplication skills? Practice is key! Use flashcards, work through practice problems, and explore different methods of visualization (arrays, number lines, etc.).
-
Are there different methods of multiplication? Yes, there are various methods, including lattice multiplication, long multiplication, and mental math techniques. Exploring these diverse methods can enhance understanding and efficiency.
Conclusion: The Enduring Significance of 3 x 2
The seemingly simple equation "3 x 2" serves as a gateway to understanding the power and versatility of multiplication. From its foundational role in arithmetic to its widespread applications in various fields, multiplication is a fundamental concept that transcends the confines of the classroom. Mastering this basic operation not only enhances mathematical proficiency but also equips individuals with a powerful tool for problem-solving in diverse aspects of life. By understanding the "why" behind the "6," we unlock a deeper appreciation for the elegance and utility of mathematics. The journey from understanding 3 x 2 to conquering complex mathematical concepts begins with a solid grasp of this fundamental building block. Continue exploring, questioning, and practicing to unlock the full potential of this seemingly simple yet profoundly significant equation.
Latest Posts
Related Post
Thank you for visiting our website which covers about 3x X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.