4x X 2
stanleys
Sep 16, 2025 · 6 min read
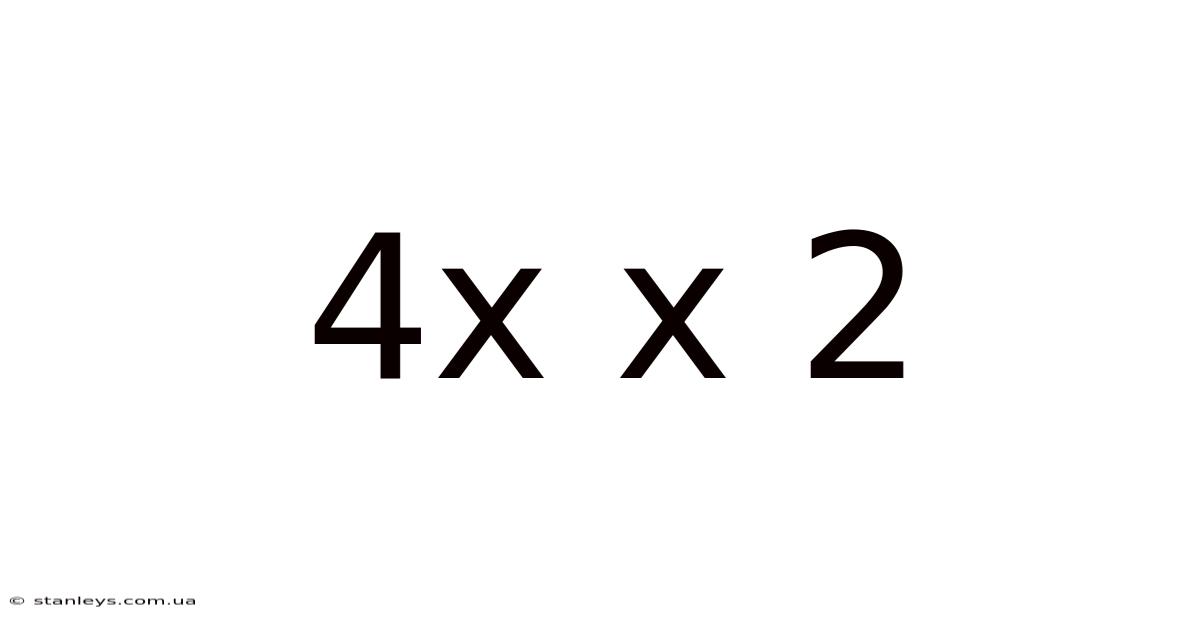
Table of Contents
Decoding 4x x 2: A Deep Dive into Multiplication and its Applications
This article explores the seemingly simple mathematical expression "4x x 2," delving beyond the basic calculation to uncover its underlying principles, diverse applications, and significance in various fields. We'll unpack the concept of multiplication, examine the specific case of 4x multiplied by 2, and explore how this fundamental operation forms the bedrock of more complex mathematical concepts and real-world scenarios. Understanding this seemingly simple equation opens doors to a wider appreciation of mathematics and its profound influence on our lives.
Understanding Multiplication: Beyond Rote Learning
Multiplication, at its core, is repeated addition. When we say "4x x 2," we're essentially saying "add 4x to itself two times." This simple understanding lays the foundation for grasping more complex multiplications. Think of it like this: you have 2 groups of 4x apples. To find the total number of apples, you would add 4x + 4x, which equals 8x. This demonstrates the essence of multiplication as a shortcut for repetitive addition. The 'x' here represents a variable, an unknown quantity that can be any number.
While basic multiplication tables are essential for fluency, true understanding goes beyond memorization. Visualizing multiplication, through diagrams, objects, or even mental imagery, enhances comprehension and allows for a more intuitive grasp of the concept. Imagine a rectangle with sides of length 4x and 2. The area of this rectangle is 4x multiplied by 2, which is 8x. This visual representation connects the abstract concept of multiplication to a tangible geometric reality.
Furthermore, understanding the commutative property of multiplication is crucial. This property states that the order of the numbers doesn't affect the result. 4x x 2 is the same as 2 x 4x; both equal 8x. This seemingly simple fact has significant implications in more advanced algebraic manipulations.
Breaking Down 4x x 2: A Step-by-Step Approach
Let's break down the calculation of 4x x 2 step-by-step:
-
Identify the Components: We have two components: 4x and 2. '4x' represents a quantity four times the value of 'x,' and '2' is a constant.
-
Apply the Multiplication: We multiply the numerical coefficient (the number in front of the variable) by the constant. In this case, 4 multiplied by 2 equals 8.
-
Retain the Variable: The variable 'x' remains unchanged throughout the process. It simply carries over to the final result.
-
Final Result: The result of 4x x 2 is 8x. This represents eight times the value of 'x.' The value of 'x' remains unknown until it's assigned a specific numerical value.
The Significance of the Variable 'x'
The presence of the variable 'x' elevates "4x x 2" beyond a simple numerical calculation. It transforms the expression into an algebraic statement, a fundamental building block of algebra. The variable 'x' can represent any number – a quantity, a measurement, or an unknown value within a problem. This makes the expression incredibly versatile and applicable in various contexts.
For instance, if 'x' represents the number of students in a classroom, then "4x x 2" could represent the total number of pencils needed if each student requires 4 pencils, and the teacher needs twice that amount. If 'x' represents the cost of a single item, "4x x 2" could denote the total cost of purchasing 8 of those items. The flexibility offered by the variable 'x' is a cornerstone of algebraic thinking.
Real-World Applications of 4x x 2 and its Principles
The principle behind 4x x 2, and multiplication in general, underpins countless real-world applications across various fields:
-
Engineering and Physics: Calculating forces, areas, volumes, and other physical quantities heavily relies on multiplication. Understanding how variables interact in multiplicative relationships is essential for accurate calculations and problem-solving in these fields. For example, calculating the area of a rectangular surface with dimensions 4x and 2 units is directly linked to this concept.
-
Finance and Business: Calculating profits, losses, interest, and taxes all involve multiplication. Understanding how different factors multiply to influence financial outcomes is crucial for making informed business decisions. For example, doubling the production (x2) of an item that costs 4x to produce directly impacts the overall budget.
-
Computer Science: Multiplication is a fundamental arithmetic operation in computer programming. It’s used in countless algorithms, calculations, and data manipulations. The efficiency of multiplication algorithms significantly impacts software performance.
-
Everyday Life: From calculating the total cost of groceries to determining the number of tiles needed for a floor, multiplication is woven into the fabric of our daily lives. It is an invisible yet powerful tool that facilitates our interactions with the world around us.
Expanding the Concept: Beyond 4x x 2
While we've focused on "4x x 2," the principles explored here are transferable to more complex scenarios. Understanding the fundamentals of multiplication with a variable allows for tackling more intricate algebraic expressions and equations. This fundamental understanding forms the basis for:
-
Solving Equations: The ability to manipulate and simplify expressions involving multiplication is crucial for solving algebraic equations. Understanding the properties of multiplication enables simplification and isolation of variables.
-
Working with Polynomials: Polynomials, expressions containing multiple terms with variables raised to different powers, utilize multiplication extensively. The ability to expand and factor polynomials relies directly on understanding the principles of multiplication.
-
Calculus: Calculus, a branch of mathematics dealing with continuous change, uses multiplication extensively in differentiation and integration – processes crucial for understanding rates of change and areas under curves.
Frequently Asked Questions (FAQ)
Q: What if 'x' is a fraction or a decimal?
A: The principles remain the same. Whether 'x' is a whole number, a fraction, or a decimal, you still multiply the numerical coefficient (4) by the constant (2) and retain the variable ('x') in the result. For example, if x = 0.5, then 4x x 2 = 4(0.5) x 2 = 4.
Q: Can 4x x 2 be simplified further?
A: Yes, the expression 4x x 2 simplifies to 8x. This is the most concise and simplified form of the expression.
Q: What is the difference between 4x x 2 and 4(x + 2)?
A: These are distinct expressions. 4x x 2 means 4 times x times 2, resulting in 8x. 4(x + 2) means 4 multiplied by the entire quantity (x + 2), requiring the distributive property: 4(x + 2) = 4x + 8.
Q: How does this relate to other mathematical operations?
A: Multiplication is closely related to other arithmetic operations such as addition, subtraction, and division. Understanding how these operations interact is essential for solving more complex mathematical problems. For instance, division is the inverse of multiplication.
Conclusion: The Enduring Power of a Simple Equation
While "4x x 2" might appear deceptively simple, its underlying principles hold immense significance across diverse fields. Understanding the concept of multiplication, the role of variables, and the interplay of numerical coefficients and constants unlocks a deeper appreciation of mathematics and its practical applications. This simple equation is not just a mathematical statement; it’s a gateway to understanding complex concepts and solving real-world problems, underscoring the profound power and versatility of mathematics. Mastering this foundational concept is key to unlocking further mathematical understanding and proficiency. The seemingly simple 8x holds the potential for much more than just a numerical answer; it represents a pathway to a world of mathematical possibilities.
Latest Posts
Related Post
Thank you for visiting our website which covers about 4x X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.