30 X 5
stanleys
Sep 13, 2025 · 6 min read
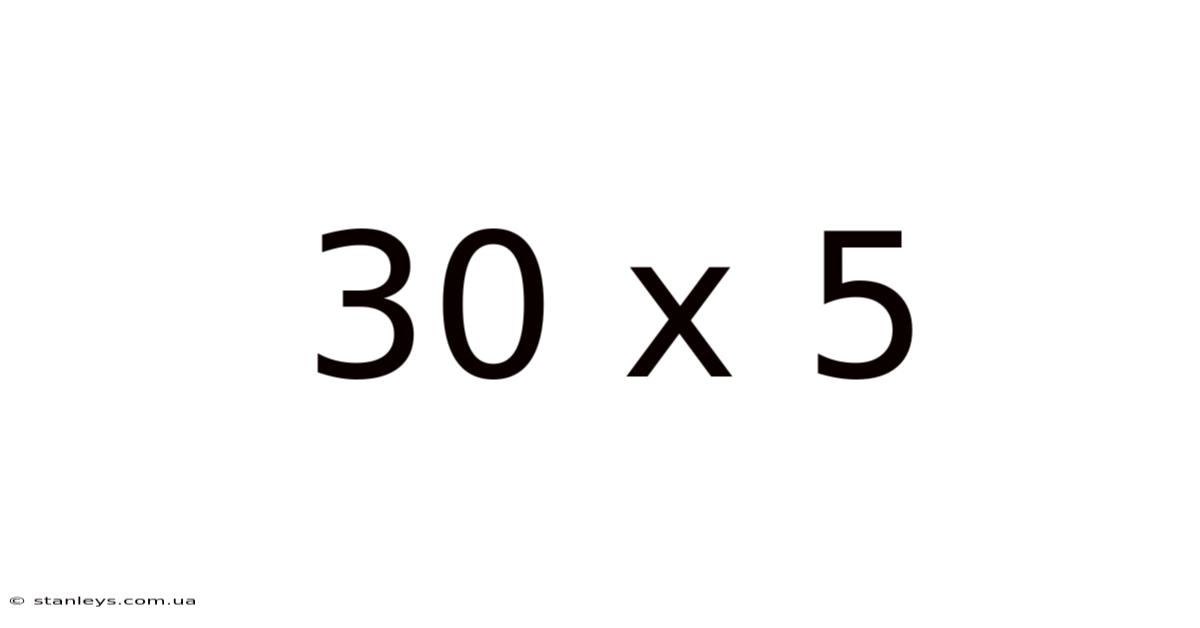
Table of Contents
Decoding 30 x 5: A Deep Dive into Multiplication and its Applications
This article explores the seemingly simple multiplication problem, 30 x 5, going far beyond a simple answer. We'll delve into the underlying mathematical concepts, explore various methods for solving it, examine its real-world applications, and even touch upon the historical context of multiplication. Whether you're a student brushing up on your arithmetic skills or an adult looking to solidify your foundational math knowledge, this comprehensive guide will provide a deeper understanding of this fundamental operation.
Introduction: Understanding the Fundamentals
The expression "30 x 5" represents a multiplication problem. Multiplication is a fundamental arithmetic operation that essentially involves repeated addition. In this case, it means adding the number 30 five times: 30 + 30 + 30 + 30 + 30. The answer, as most will readily know, is 150. However, understanding why the answer is 150 and exploring different approaches to arrive at this solution is key to grasping the broader concepts of mathematics. This exploration will extend our understanding beyond simple arithmetic to encompass more complex applications. We’ll cover various methods including standard multiplication, using place value, and exploring visual representations.
Methods for Solving 30 x 5
Several approaches can be used to solve 30 x 5. Let's examine some of them:
-
Standard Multiplication: This is the most common method taught in schools. We multiply the units digit (0) by 5, resulting in 0. Then we multiply the tens digit (3) by 5, resulting in 15. Combining these results gives us 150.
-
Distributive Property: This method breaks down the problem into smaller, more manageable parts. We can rewrite 30 as (3 x 10). Therefore, 30 x 5 becomes (3 x 10) x 5. Using the associative property of multiplication, we can rearrange this as 3 x (10 x 5), which simplifies to 3 x 50 = 150. This method demonstrates a crucial property of multiplication that's essential for understanding more advanced algebraic concepts.
-
Repeated Addition: As mentioned earlier, multiplication is essentially repeated addition. Adding 30 five times (30 + 30 + 30 + 30 + 30) directly yields the answer, 150. This method is especially helpful for visualizing the concept of multiplication, particularly for younger learners.
-
Place Value Understanding: Understanding place value is crucial. We can break down 30 into its tens and units place: 3 tens and 0 units. Multiplying the tens place (3 tens) by 5 gives us 15 tens, which is equal to 150. This emphasizes the importance of understanding the value of digits based on their position within a number.
-
Visual Representations: Visual aids can be highly beneficial, especially for visual learners. Imagine 5 rows of 30 objects each. Counting all the objects would give you 150, providing a concrete representation of the multiplication problem. Similarly, using array models (grids) where one side represents 30 and the other 5 can provide a clear visual solution.
Real-World Applications of 30 x 5
The seemingly simple calculation of 30 x 5 has numerous real-world applications across various domains:
-
Shopping: Imagine buying 5 items that cost $30 each. The total cost would be 30 x 5 = $150. This applies to any scenario involving multiple purchases of identically priced items.
-
Measurement: Converting units often involves multiplication. For example, if a rectangular garden measures 30 feet in length and 5 feet in width, its area would be 30 x 5 = 150 square feet. This can be applied to calculating areas of rooms, fields, and other surfaces.
-
Finance: Calculating interest, monthly payments, or total earnings often involves multiplication. For instance, if you save $30 a week for 5 weeks, your total savings would be 30 x 5 = $150.
-
Time Management: If a task takes 30 minutes and you need to repeat it 5 times, the total time required would be 30 x 5 = 150 minutes, or 2.5 hours. This principle is essential for project planning and time allocation.
-
Recipe Scaling: When cooking, you might need to increase a recipe's quantities. If a recipe calls for 30 grams of flour and you want to make 5 times the quantity, you'd need 30 x 5 = 150 grams of flour.
-
Manufacturing and Production: In factories and manufacturing plants, calculating the total number of products produced, materials needed, or man-hours required often involves multiplication. For instance, if a machine produces 30 units per hour and runs for 5 hours, it will produce 30 x 5 = 150 units.
The Historical Context of Multiplication
Multiplication, as a concept, has evolved over centuries. Ancient civilizations developed various methods for performing multiplication, often without the familiar algorithms we use today. Some early methods included:
-
Egyptian Multiplication: This method used a system of doubling and adding to perform multiplication.
-
Babylonian Multiplication: The Babylonians used a sexagesimal system (base-60) and developed multiplication tables for their calculations.
-
Roman Multiplication: The Romans used various methods, often relying on a combination of addition and subtraction.
The development of modern multiplication algorithms, including the standard method we use today, reflects centuries of mathematical advancements and refinements. Understanding the historical context enhances our appreciation for the sophistication of modern mathematical tools.
Advanced Concepts and Extensions
While 30 x 5 is a basic multiplication problem, it serves as a stepping stone to more complex mathematical concepts:
-
Algebra: The principles of multiplication extend directly into algebra. Understanding how to manipulate equations involving multiplication is fundamental to solving algebraic problems.
-
Calculus: Calculus builds upon foundational arithmetic operations, including multiplication. Derivatives and integrals rely on the understanding of limits and rates of change, which are built upon multiplication and other arithmetic operations.
-
Statistics: Statistical calculations often involve multiplication, particularly in calculating probabilities, means, and variances.
-
Geometry: Calculating areas and volumes frequently involves multiplication. The area of a rectangle, for example, is found by multiplying its length and width.
Frequently Asked Questions (FAQ)
-
What are the factors of 150? The factors of 150 are 1, 2, 3, 5, 6, 10, 15, 25, 30, 50, 75, and 150.
-
Is 30 x 5 the same as 5 x 30? Yes, this demonstrates the commutative property of multiplication: the order of the numbers being multiplied does not affect the result.
-
How can I explain 30 x 5 to a young child? Use visual aids like counters or drawings. Show them 5 groups of 30 objects and count them together. Repeated addition is also a helpful approach.
-
Are there any online tools or calculators for multiplication? Yes, many online calculators and educational websites provide tools to practice multiplication and check answers.
Conclusion: The Significance of 30 x 5
While seemingly simple, the multiplication problem 30 x 5 reveals a wealth of mathematical concepts and real-world applications. Understanding different methods for solving it, appreciating its historical context, and exploring its connections to more advanced mathematical fields strengthens our overall mathematical foundation. This exploration serves not just to provide the answer (150), but to illustrate the beauty and power of multiplication as a fundamental building block of mathematics and its pervasive presence in our daily lives. By understanding the 'why' behind the 'what', we move beyond simple calculation to a deeper, more meaningful understanding of the mathematical world around us. This understanding extends beyond simple arithmetic, providing a solid base for tackling more challenging mathematical problems in the future.
Latest Posts
Latest Posts
-
181cm In Foot
Sep 13, 2025
-
37 X 4
Sep 13, 2025
-
93 Kilometers Miles
Sep 13, 2025
-
27000 12
Sep 13, 2025
-
82 X 3
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 30 X 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.