37 X 4
stanleys
Sep 13, 2025 · 5 min read
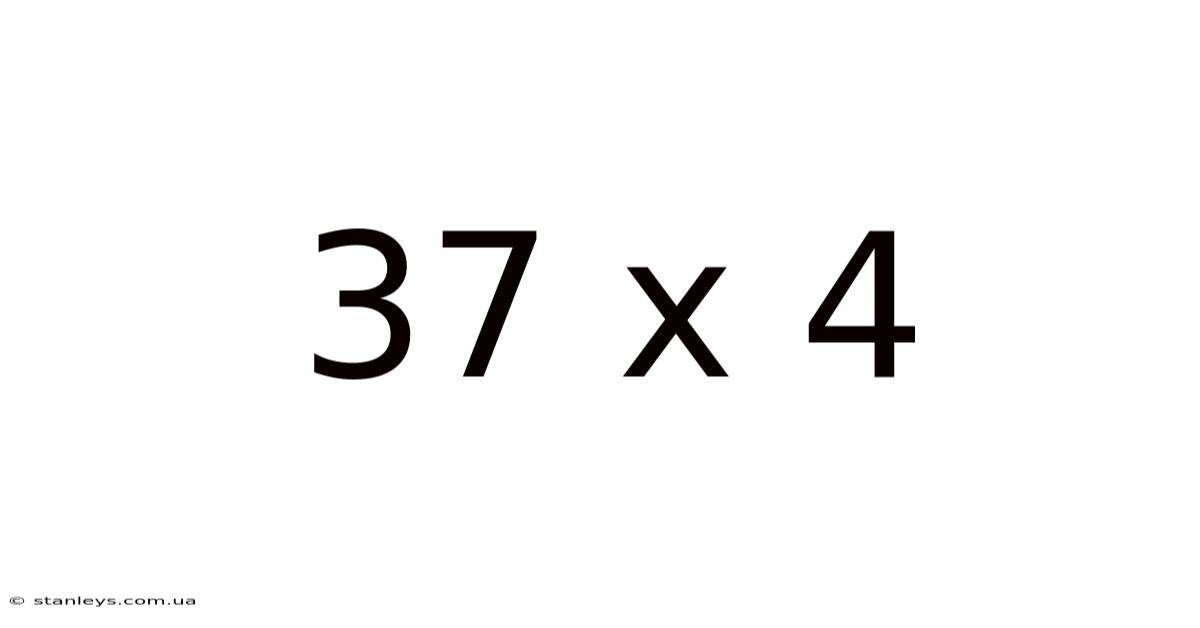
Table of Contents
Unlocking the Mystery of 37 x 4: A Deep Dive into Multiplication
This article explores the seemingly simple multiplication problem, 37 x 4, in a comprehensive and engaging manner. We'll move beyond a simple answer, delving into various methods of solving this problem, exploring the underlying mathematical concepts, and examining its applications in real-world scenarios. Understanding 37 x 4 is not just about getting the right answer; it's about grasping fundamental mathematical principles that underpin more complex calculations. This exploration is suitable for students of all levels, from elementary school to those seeking a refresher on basic arithmetic.
Understanding the Fundamentals: Multiplication as Repeated Addition
At its core, multiplication is a shortcut for repeated addition. When we see 37 x 4, we're essentially asking: "What is the sum of four 37s?" This can be visually represented as:
37 + 37 + 37 + 37 = ?
This approach, while straightforward, becomes cumbersome with larger numbers. Therefore, understanding more efficient methods is crucial.
Method 1: Standard Multiplication Algorithm
This is the method most commonly taught in schools. It involves breaking down the numbers into tens and ones, multiplying each part separately, and then adding the results.
- Step 1: Multiply the ones: 4 x 7 = 28. Write down the '8' and carry-over the '2'.
- Step 2: Multiply the tens: 4 x 3 = 12. Add the carried-over '2': 12 + 2 = 14.
- Step 3: Combine the results: The final answer is 148.
Therefore, 37 x 4 = 148. This method relies on place value understanding, a cornerstone of arithmetic.
Method 2: Distributive Property
The distributive property states that multiplying a sum by a number is the same as multiplying each addend by the number and then adding the products. We can apply this to 37 x 4:
37 x 4 = (30 + 7) x 4 = (30 x 4) + (7 x 4) = 120 + 28 = 148
This method showcases the flexibility of mathematical operations and provides a deeper understanding of why the standard algorithm works. It's particularly useful for breaking down more complex multiplications.
Method 3: Doubling and Halving
This method involves repeatedly doubling and halving the numbers until you reach a simpler calculation. It's based on the associative property of multiplication. While not directly applicable to 37 x 4 in a straightforward manner (37 isn't easily halved), it's a valuable technique for understanding different approaches to multiplication. Consider a similar problem like 14 x 8:
We can halve 14 to get 7, and double 8 to get 16. Now we have 7 x 16. We can double 7 to 14 and halve 16 to 8, giving us 14 x 8 (back to the original problem). While not simplifying this specific example directly, the concept highlights the flexibility of manipulating numbers in multiplication. This technique is highly effective with even numbers and those easily divisible by 2.
Method 4: Lattice Multiplication
Lattice multiplication, an ancient method, provides a visual approach to multiplication. It's especially helpful for larger numbers and for demonstrating place value. While less efficient for 37 x 4, it's illustrative of different mathematical approaches.
Method 5: Using a Calculator
While not a mathematical method in itself, calculators provide a quick and efficient way to verify calculations, especially for larger numbers. For 37 x 4, a calculator instantly returns the answer 148. However, relying solely on calculators without understanding the underlying principles hinders true mathematical comprehension.
Real-World Applications of 37 x 4
While seemingly simple, the concept of multiplication applies broadly in everyday life:
- Shopping: Calculating the total cost of four items priced at $37 each.
- Measurement: Determining the total length of four pieces of wood, each 37 inches long.
- Baking: Calculating the amount of an ingredient needed if a recipe calls for 37 grams four times.
- Travel: Determining the total distance traveled over four days if you travel 37 kilometers each day.
Expanding on the Concept: Multiplication with Larger Numbers
Understanding 37 x 4 is a stepping stone to mastering more complex multiplications. The principles learned – repeated addition, distributive property, place value – are essential for tackling larger numbers. Consider the process of multiplying 37 x 400:
This can be approached as (37 x 4) x 100 = 148 x 100 = 14800. This showcases how understanding smaller multiplication problems facilitates tackling larger ones. Similarly, multiplying 37 by a decimal number builds on the same foundational principles.
Frequently Asked Questions (FAQ)
-
Q: Why is multiplication important? A: Multiplication is a fundamental arithmetic operation used extensively in various fields, from everyday calculations to advanced mathematics and science. It simplifies repeated addition and provides efficient ways to solve complex problems.
-
Q: Are there other ways to solve 37 x 4? A: Yes, various methods exist, including the use of visual aids, alternative algorithms, and the application of different mathematical properties. The best method often depends on individual preference and the complexity of the problem.
-
Q: What if I make a mistake in my calculation? A: Mistakes are a natural part of the learning process. Double-check your work, use alternative methods to verify your answer, or seek help from a teacher or tutor.
-
Q: How can I improve my multiplication skills? A: Practice regularly, use different methods to understand the concept deeply, and gradually increase the complexity of the problems you solve.
Conclusion: Mastering the Basics, Reaching for the Future
While 37 x 4 may seem like a simple problem, its exploration reveals fundamental mathematical principles vital for success in higher-level mathematics. By understanding various solution methods and appreciating the real-world applications of multiplication, students can build a strong foundation for future learning and problem-solving. Mastering the seemingly simple unlocks the ability to conquer more complex challenges. Remember, the journey of understanding mathematics is a process of building upon fundamental concepts, one calculation at a time. The ability to confidently and accurately solve 37 x 4 is not just about the answer; it’s about the journey towards mathematical proficiency and a deeper appreciation for the power of numbers. The simplicity of this problem belies its importance as a building block in a larger mathematical framework.
Latest Posts
Latest Posts
-
30 Off 55
Sep 13, 2025
-
9 2 Decimal
Sep 13, 2025
-
1 78m In Feet
Sep 13, 2025
-
7 8 6
Sep 13, 2025
-
140km To Miles
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 37 X 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.