82 X 3
stanleys
Sep 13, 2025 · 5 min read
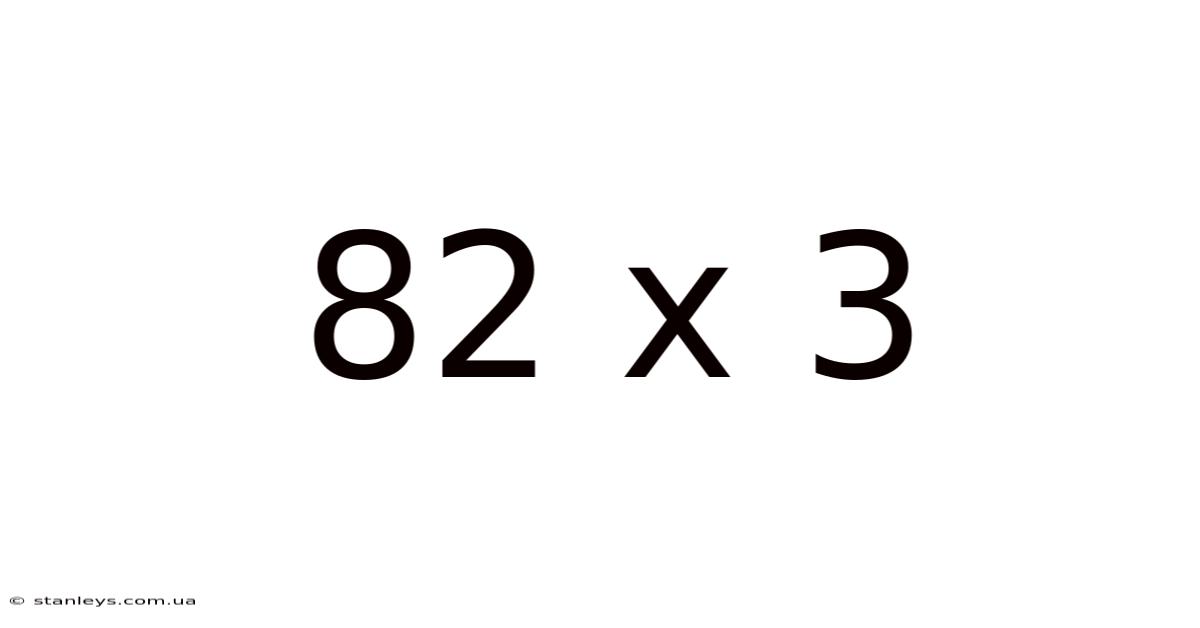
Table of Contents
Exploring the Multiplication Problem: 82 x 3 – A Deep Dive into Calculation and Concepts
This article delves into the seemingly simple multiplication problem of 82 x 3, transforming it from a basic arithmetic exercise into an exploration of fundamental mathematical concepts. We'll examine various methods for solving this problem, from traditional techniques to more advanced strategies, providing a comprehensive understanding applicable to more complex calculations. This exploration is ideal for anyone looking to solidify their grasp of multiplication, improve their computational skills, or gain a deeper appreciation for the underlying principles of mathematics. We'll uncover the beauty and logic inherent in even the most basic arithmetic operations.
Introduction: The Power of Multiplication
Multiplication, at its core, represents repeated addition. When we say 82 x 3, we're essentially asking: what is the sum of three 82s? This seemingly straightforward question opens doors to numerous mathematical concepts, including place value, distributive property, and different calculation strategies. Understanding these concepts provides a robust foundation for tackling more intricate mathematical problems later on. This article will illuminate these principles using the example of 82 x 3.
Method 1: Traditional Long Multiplication
This is the method most of us learn in elementary school. It systematically breaks down the multiplication into smaller, manageable steps.
-
Set up the problem: Write 82 on top and 3 below, aligning the digits correctly.
82 x 3 --- -
Multiply the ones digit: Multiply the ones digit of 82 (2) by 3. 2 x 3 = 6. Write 6 below the line.
82 x 3 --- 6 -
Multiply the tens digit: Multiply the tens digit of 82 (8) by 3. 8 x 3 = 24. Write 24 to the left of the 6.
82 x 3 --- 246 -
The answer: The result of 82 x 3 is 246.
This method demonstrates the distributive property in action. We are essentially calculating (80 x 3) + (2 x 3) = 240 + 6 = 246.
Method 2: Breaking Down the Numbers
This approach utilizes the distributive property more explicitly. We can break down 82 into its constituent parts (80 + 2) and then multiply each part by 3.
-
Separate the tens and ones: Rewrite 82 as 80 + 2.
-
Multiply each part: (80 x 3) + (2 x 3)
-
Calculate: 240 + 6 = 246
This method highlights the underlying principle of distributing the multiplication across the summands, reinforcing the distributive property of multiplication over addition. This is a valuable skill for mental math and solving more complex problems.
Method 3: Repeated Addition
This method directly reflects the definition of multiplication as repeated addition. We add 82 three times.
82 + 82 + 82 = 246
While simple for smaller numbers, this method becomes less efficient with larger numbers. It serves as a valuable reminder of the fundamental connection between addition and multiplication.
Method 4: Lattice Multiplication
Lattice multiplication is a visual method particularly useful for larger numbers. Though less commonly taught, it offers a systematic approach that reduces the likelihood of errors.
-
Create the lattice: Draw a grid with two columns (for the tens and ones digits of 82) and one row (for the multiplier 3).
-
Multiply and place diagonals: Multiply each digit of 82 by 3 and place the result in the corresponding cell, splitting the tens and ones digit across the diagonal.
+---+---+ | 2 | 4 | +---+---+ | | 6 | +---+---+ -
Sum the diagonals: Add the numbers along the diagonals, starting from the bottom right.
6 + 4 = 10 (write down 0, carry-over 1) 1 + 2 = 3 Total: 246
Lattice multiplication is a powerful tool for managing carrying and visualizing the multiplication process, making it less prone to mistakes compared to traditional methods.
Understanding Place Value: The Significance of Digits
The problem 82 x 3 directly illustrates the importance of place value in our number system. The digit 8 represents 80 (eighty) and the digit 2 represents 2 (two). When we multiply, we are essentially multiplying each place value separately and then combining the results. This understanding is crucial not only for multiplication but also for all arithmetic operations involving multi-digit numbers.
The Distributive Property: A Cornerstone of Algebra
The distributive property, represented as a(b + c) = ab + ac, is a fundamental concept in algebra. We've already seen it in action with our different methods for solving 82 x 3. This property is a powerful tool for simplifying expressions and solving equations, making it a key concept to master for further mathematical studies.
Expanding the Concept: Applying to Larger Numbers
The methods discussed above can be applied to much larger multiplication problems. Breaking down large numbers into smaller, manageable parts (using the distributive property) makes complex calculations much more approachable. This strategy is key to developing mental math skills and efficient problem-solving techniques.
Frequently Asked Questions (FAQ)
-
Q: Why is multiplication important? A: Multiplication is fundamental to numerous aspects of our lives, from calculating costs and areas to understanding proportions and scales. It's a cornerstone of mathematics and essential for many scientific and engineering applications.
-
Q: Are there any other methods for solving 82 x 3? A: While the methods outlined above are the most common and effective, alternative strategies exist, often involving the use of different number bases or visual representations.
-
Q: How can I improve my multiplication skills? A: Practice is key! Regularly work through multiplication problems of varying difficulty. Use different methods to solidify your understanding and find the approach that suits you best.
-
Q: What if I'm struggling with multiplication? A: Don't be discouraged! Seek help from teachers, tutors, or online resources. Breaking down complex problems into smaller steps and focusing on the underlying principles can help overcome challenges.
Conclusion: Beyond the Numbers
The seemingly simple problem of 82 x 3 offers a rich landscape for exploring fundamental mathematical concepts. From traditional long multiplication to the distributive property and the significance of place value, this problem provides a solid foundation for understanding more complex mathematical operations. By mastering these concepts and employing various calculation methods, we not only improve our arithmetic skills but also develop a deeper appreciation for the elegance and logic inherent in mathematics. The ability to approach a problem from multiple angles – from simple addition to leveraging the distributive property and even the visual representation of lattice multiplication – empowers us to become more versatile and efficient mathematicians. Remember, mathematics is not just about memorization; it's about understanding the underlying principles and applying them creatively to solve problems. This understanding will serve you well in any future mathematical endeavors.
Latest Posts
Latest Posts
-
30 Off 55
Sep 13, 2025
-
9 2 Decimal
Sep 13, 2025
-
1 78m In Feet
Sep 13, 2025
-
7 8 6
Sep 13, 2025
-
140km To Miles
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 82 X 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.