30 Of 120
stanleys
Sep 13, 2025 · 5 min read
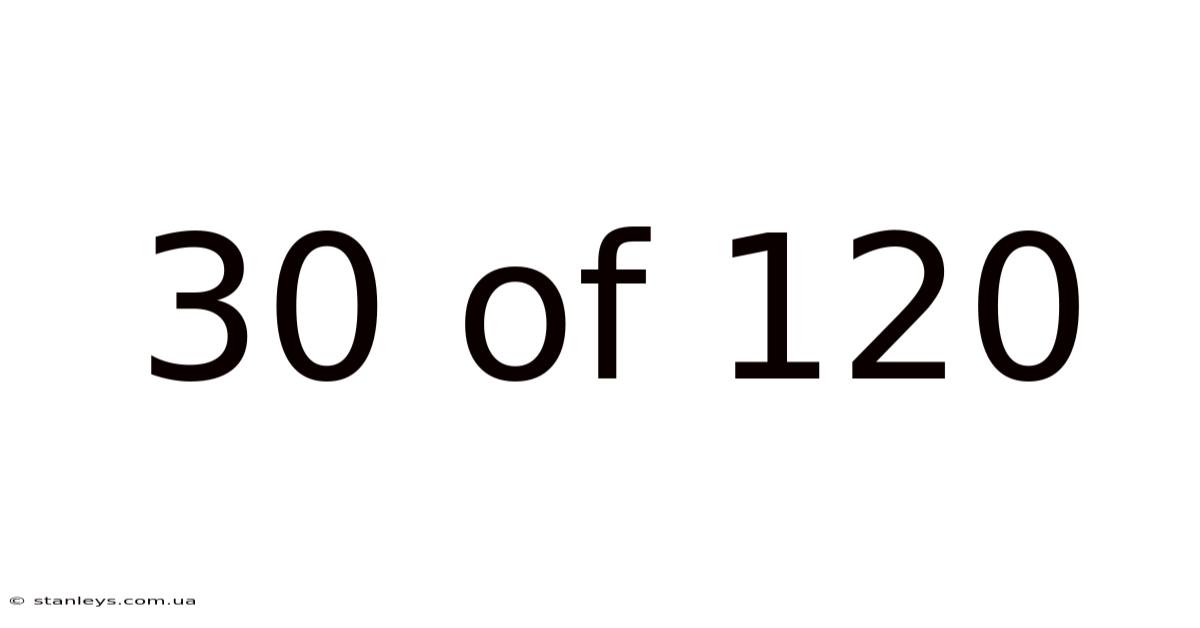
Table of Contents
Decoding 30/120: Understanding Fractions, Ratios, and Percentages
Understanding fractions, ratios, and percentages is fundamental to many aspects of life, from baking a cake to analyzing financial data. This article will delve into the meaning of "30/120," explaining its various interpretations and applications, and demonstrating how to simplify, convert, and utilize this fractional representation in different contexts. We'll explore the core mathematical concepts involved and provide practical examples to solidify your understanding.
What Does 30/120 Represent?
The expression "30/120" represents a fraction, indicating a part-to-whole relationship. It signifies 30 out of 120 equal parts. This fraction can be interpreted in several ways, depending on the context:
-
Part of a Whole: 30/120 represents 30 parts out of a total of 120 parts. Imagine dividing a pizza into 120 slices; 30/120 represents 30 of those slices.
-
Ratio: It can be viewed as a ratio of 30 to 120, expressing a comparison between two quantities. This could represent, for instance, the ratio of red marbles to the total number of marbles in a bag.
-
Probability: In probability, 30/120 could represent the probability of a specific event occurring, given 30 favorable outcomes out of 120 possible outcomes.
Simplifying the Fraction
Before exploring further applications, it's essential to simplify the fraction 30/120. This involves finding the greatest common divisor (GCD) of both the numerator (30) and the denominator (120) and dividing both by it.
The prime factorization of 30 is 2 x 3 x 5. The prime factorization of 120 is 2 x 2 x 2 x 3 x 5.
The GCD of 30 and 120 is 2 x 3 x 5 = 30.
Dividing both the numerator and the denominator by 30, we get:
30/120 = (30 ÷ 30) / (120 ÷ 30) = 1/4
Therefore, the simplified form of the fraction 30/120 is 1/4. This simplified form makes calculations and comparisons much easier.
Converting to a Percentage
To express 30/120 (or its simplified form, 1/4) as a percentage, we multiply the fraction by 100%:
(1/4) x 100% = 25%
This means that 30 out of 120 represents 25% of the whole.
Real-World Applications of 30/120 (or 1/4 or 25%)
The fraction 30/120, and its simplified equivalent 1/4 or 25%, has numerous applications across various fields:
-
Finance: Imagine a company's stock price drops from $120 to $90. The decrease is $30. The percentage decrease is calculated as (30/120) x 100% = 25%.
-
Sales and Marketing: If a store sells 30 out of 120 items of a particular product, the sales percentage is 25%. This data helps businesses understand product demand and adjust inventory accordingly.
-
Education: In a class of 120 students, if 30 students score above 90%, the percentage of high-achieving students is 25%. This helps educators assess the effectiveness of their teaching methods.
-
Sports: If a basketball player makes 30 out of 120 attempted shots, their shooting percentage is 25%.
-
Surveys and Polls: If 30 out of 120 respondents chose a particular option in a survey, the percentage of respondents choosing that option is 25%.
-
Recipe Scaling: A recipe calling for 30 grams of sugar in a total of 120 grams of ingredients implies that sugar constitutes 25% of the recipe's weight. This can be used to scale the recipe up or down proportionally.
Understanding Proportions
The concept of proportions is closely linked to fractions and ratios. A proportion is a statement that two ratios are equal. We can use proportions to solve various problems involving 30/120.
For example: If 30 out of 120 students in a school are left-handed, how many left-handed students would we expect in a school with 360 students?
We can set up a proportion:
30/120 = x/360
Cross-multiplying, we get:
120x = 30 * 360
x = (30 * 360) / 120
x = 90
Therefore, we would expect 90 left-handed students in a school with 360 students.
Working with Different Units
The fraction 30/120 can also be applied to quantities with different units. For instance:
-
Time: If a project takes 120 hours, and 30 hours have already been completed, then 25% of the project is finished.
-
Distance: If a journey is 120 kilometers, and 30 kilometers have been traveled, then 25% of the journey is complete.
Frequently Asked Questions (FAQ)
Q1: Can I simplify 30/120 to a different fraction besides 1/4?
A1: While 1/4 is the simplest form, you can express it as equivalent fractions like 2/8, 3/12, or 5/20, but these are less efficient for calculations.
Q2: How do I convert a percentage back to a fraction?
A2: To convert a percentage (like 25%) to a fraction, divide the percentage by 100 and simplify: 25%/100 = 25/100 = 1/4.
Q3: What if the numerator is larger than the denominator in a fraction?
A3: If the numerator is larger than the denominator (e.g., 120/30), the fraction is an improper fraction. This represents a value greater than 1. It can be converted into a mixed number (a whole number and a proper fraction) or an equivalent decimal. For example, 120/30 simplifies to 4, representing 4 whole units.
Q4: How does understanding 30/120 help in everyday life?
A4: Understanding fractions and percentages is crucial for budgeting, calculating discounts, understanding statistics, interpreting data in various fields, and solving everyday problems involving ratios and proportions.
Conclusion: The Power of Understanding Fractions
The seemingly simple fraction 30/120 embodies fundamental mathematical concepts with broad practical applications. By understanding how to simplify, convert, and interpret fractions, ratios, and percentages, you equip yourself with essential skills applicable to diverse areas of life, from personal finance to advanced scientific studies. Mastering these core concepts empowers you to analyze data, solve problems, and make informed decisions more effectively. Remember that practice is key; the more you work with these concepts, the more intuitive they will become. Don't be afraid to tackle different problems and explore various contexts where fractions and percentages play a vital role. The ability to work comfortably with these concepts is a valuable asset in navigating the complexities of the world around us.
Latest Posts
Latest Posts
-
10 Of 480
Sep 13, 2025
-
3 8 Of 48
Sep 13, 2025
-
60miles In Km
Sep 13, 2025
-
Cost Of Chloroform
Sep 13, 2025
-
8 Of 2400
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 30 Of 120 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.