3/8 Of 48
stanleys
Sep 13, 2025 · 5 min read
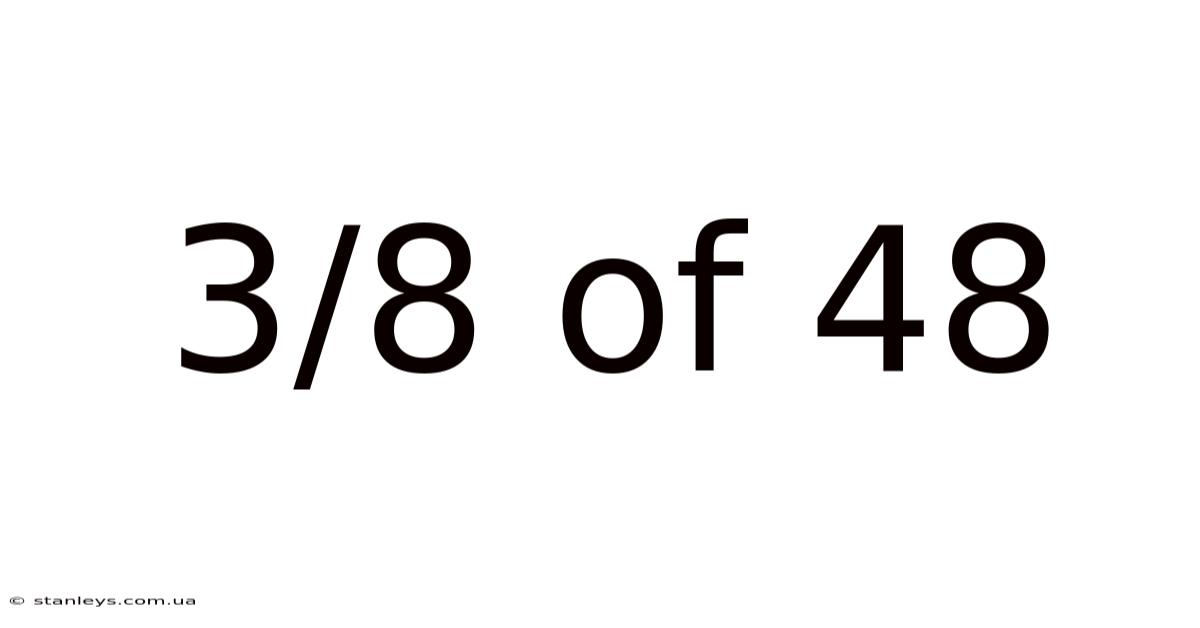
Table of Contents
Unveiling the Mystery: A Deep Dive into 3/8 of 48
Finding 3/8 of 48 might seem like a simple arithmetic problem, suitable only for elementary school. However, this seemingly straightforward calculation offers a fantastic opportunity to explore fundamental mathematical concepts, delve into different solution methods, and even touch upon the practical applications of fractions in everyday life. This article will guide you through various ways to solve this problem, explain the underlying mathematical principles, and explore its broader relevance. By the end, you'll not only know the answer but also possess a deeper understanding of fractions and their operations.
Understanding Fractions: The Building Blocks
Before tackling 3/8 of 48, let's refresh our understanding of fractions. A fraction represents a part of a whole. It consists of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into. In our problem, 3/8, 3 is the numerator and 8 is the denominator. This means we're interested in 3 out of 8 equal parts of a whole.
Method 1: Direct Multiplication
The most straightforward approach to finding 3/8 of 48 is through direct multiplication. We can express "of" as multiplication. Therefore, the problem becomes:
(3/8) * 48
To perform this multiplication, we can either convert 48 into a fraction (48/1) and multiply the numerators and denominators:
(3/8) * (48/1) = (3 * 48) / (8 * 1) = 144 / 8
Then, we simplify the fraction by dividing the numerator by the denominator:
144 / 8 = 18
Therefore, 3/8 of 48 is 18.
Method 2: Finding One-Eighth First
Alternatively, we can break down the problem into smaller, more manageable steps. First, we find 1/8 of 48 by dividing 48 by 8:
48 / 8 = 6
This means 1/8 of 48 is 6. Since we want 3/8, we simply multiply the value of 1/8 by 3:
6 * 3 = 18
This method provides a clear, step-by-step approach, making it easier to visualize and understand the process. It's particularly helpful for those who find direct fraction multiplication challenging.
Method 3: Simplifying Before Multiplication
Before performing the multiplication, we can simplify the fraction to make the calculation easier. Notice that 48 is divisible by 8:
48 / 8 = 6
We can rewrite the problem as:
(3/8) * 48 = 3 * (48/8) = 3 * 6 = 18
This method highlights the importance of simplifying fractions whenever possible to reduce computational complexity.
Visual Representation: Understanding Fractions Concretely
Let's visualize this problem. Imagine a pizza cut into 8 equal slices. 3/8 of the pizza represents 3 out of those 8 slices. If the whole pizza has 48 pieces of pepperoni (representing the total of 48), each slice would have 6 pieces (48/8 = 6). Therefore, 3 slices would have 18 pieces of pepperoni (6 * 3 = 18). This visual representation makes the abstract concept of fractions more concrete and understandable.
Fractions in Real-World Applications
Understanding fractions is crucial for various real-world applications. From cooking and baking (following recipes that require fractional measurements) to calculating discounts and sales tax, fractions are an integral part of our daily lives. Imagine needing to calculate a 3/8 discount on a $48 item. Using the methods outlined above, you would easily determine the discount amount to be $18. This demonstrates the practical relevance of understanding fraction calculations.
Expanding the Concept: Working with Different Fractions and Numbers
The methods discussed above can be applied to any fraction and number. Let's try another example: finding 2/5 of 75.
Method 1 (Direct Multiplication):
(2/5) * 75 = (2 * 75) / 5 = 150 / 5 = 30
Method 2 (Finding One-Fifth First):
75 / 5 = 15 (one-fifth of 75) 15 * 2 = 30 (two-fifths of 75)
Method 3 (Simplifying Before Multiplication):
(2/5) * 75 = 2 * (75/5) = 2 * 15 = 30
These examples reinforce the versatility and applicability of the methods explained earlier.
Decimal Equivalents and Percentage Representation
It's important to understand that fractions can also be expressed as decimals and percentages. The fraction 3/8 is equivalent to 0.375 in decimal form. To convert this to a percentage, we multiply by 100:
0.375 * 100 = 37.5%
Therefore, 3/8 of 48 is also equivalent to 37.5% of 48, which is still 18. This shows the interconnectivity of different mathematical representations.
Addressing Common Misconceptions
A common misconception when working with fractions is the order of operations. It's crucial to remember that multiplication and division should be performed before addition and subtraction. In our problem, we multiply the fraction by 48 before considering any other operations. Another misconception involves simplifying fractions; always simplify before multiplying to make the calculation more efficient and less prone to errors.
Frequently Asked Questions (FAQ)
-
Q: Can I use a calculator to solve this problem? A: Yes, you can use a calculator to perform the multiplication and division steps, but understanding the underlying concepts is crucial for applying these skills to more complex problems.
-
Q: What if the fraction and number are not easily divisible? A: You can still use the methods outlined above; the calculation might involve more complex division or simplification, but the principles remain the same.
-
Q: Are there other ways to solve this problem? A: While the methods discussed are the most efficient and commonly used, other approaches exist, such as using proportions or visual aids.
Conclusion: Mastering Fractions for a Brighter Future
Finding 3/8 of 48, while seemingly simple, serves as a valuable stepping stone to mastering fundamental mathematical concepts. By understanding different solution methods, visualizing the problem, and appreciating its real-world applications, we can build a solid foundation in fractions and enhance our problem-solving skills. This knowledge extends far beyond simple arithmetic, providing a crucial base for more advanced mathematical concepts and real-world applications. Remember, the key is not just to find the answer (which is 18), but to understand why and how you arrived at that answer. This deeper understanding empowers you to tackle more complex mathematical challenges with confidence and competence.
Latest Posts
Latest Posts
-
20 Of 4500
Sep 13, 2025
-
30 Of 75
Sep 13, 2025
-
70 Of 7
Sep 13, 2025
-
Crown At Hallow
Sep 13, 2025
-
3 3kg In Lbs
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 3/8 Of 48 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.