10 Of 480
stanleys
Sep 13, 2025 · 5 min read
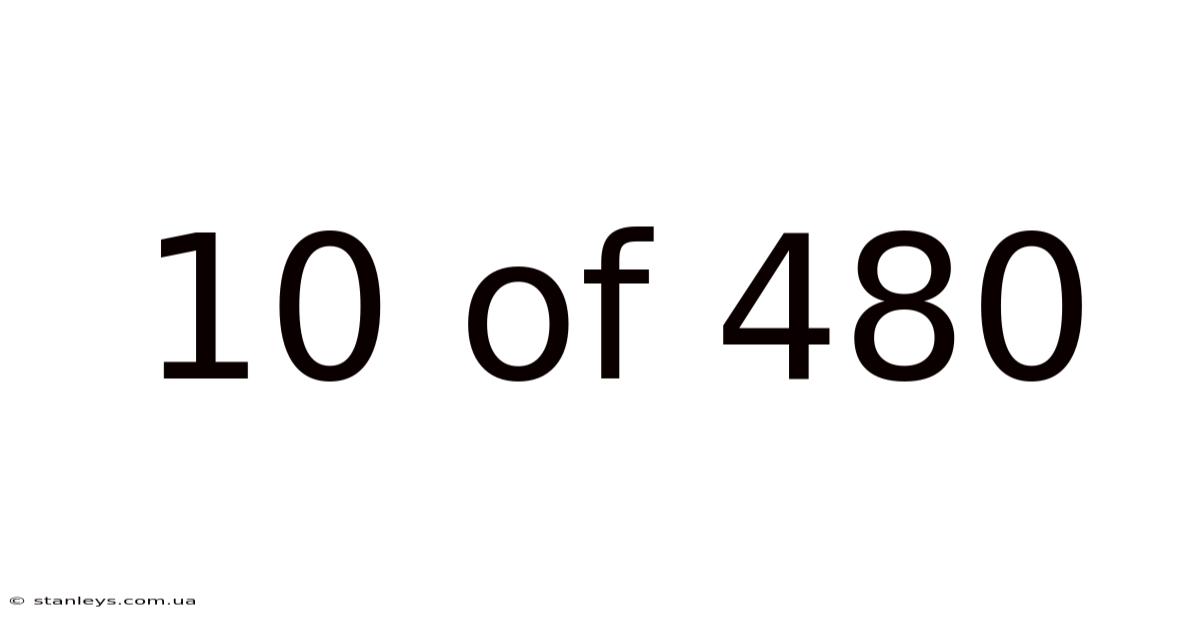
Table of Contents
Decoding the Enigma: Understanding the Fraction 10/480 and its Applications
The seemingly simple fraction 10/480 might appear insignificant at first glance. However, understanding this fraction, simplifying it, and exploring its applications unveils a deeper understanding of mathematical concepts and their real-world relevance. This article will delve into the intricacies of 10/480, exploring its simplification, equivalent representations, and practical applications across various fields. We will also explore how understanding fractions like this can build a strong foundation in mathematical reasoning.
Introduction: Simplifying Fractions – A Foundational Skill
Before we embark on the journey of deciphering 10/480, let's refresh our understanding of fraction simplification. A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). Simplifying a fraction means reducing it to its lowest terms, while maintaining its value. This is achieved by finding the greatest common divisor (GCD) of the numerator and the denominator and dividing both by it. This process makes the fraction easier to understand and work with.
Simplifying 10/480: Finding the GCD
To simplify 10/480, we need to find the greatest common divisor (GCD) of 10 and 480. The GCD is the largest number that divides both 10 and 480 without leaving a remainder. We can find the GCD using several methods, including prime factorization or the Euclidean algorithm.
Let's use prime factorization. The prime factorization of 10 is 2 x 5. The prime factorization of 480 is 2 x 2 x 2 x 2 x 2 x 3 x 5. The common factors are 2 and 5. Therefore, the GCD of 10 and 480 is 2 x 5 = 10.
Now, we divide both the numerator and the denominator by the GCD:
10 ÷ 10 = 1 480 ÷ 10 = 48
Therefore, the simplified form of 10/480 is 1/48.
Equivalent Representations of 1/48
While 1/48 is the simplest form, it's essential to understand that this fraction can be represented in other equivalent forms by multiplying both the numerator and the denominator by the same number. For instance:
- 2/96 (multiplying both by 2)
- 3/144 (multiplying both by 3)
- 5/240 (multiplying both by 5)
All these fractions are equivalent to 1/48 and represent the same proportion or part of a whole.
Visualizing 1/48: A Practical Approach
Understanding fractions is often easier with a visual representation. Imagine a pizza cut into 48 equal slices. The fraction 1/48 represents just one of those 48 slices. This visual aids in grasping the magnitude of the fraction and its relationship to the whole.
Practical Applications of 1/48 and its Equivalent Fractions
While 1/48 might seem like a small fraction, its applications are surprisingly diverse across numerous fields:
-
Probability and Statistics: If there's a 1/48 chance of winning a lottery, it represents a low probability. Understanding this fraction helps assess the likelihood of an event.
-
Measurement and Engineering: In engineering and construction, precise measurements are crucial. 1/48 might represent a small tolerance in a dimension, or a small portion of a larger component. This fraction helps ensure accuracy and precision in designs.
-
Chemistry and Physics: In chemical solutions or physics experiments, fractions like 1/48 might represent the ratio of components in a mixture or the proportion of a substance in a reaction. Precise measurements are crucial here to ensure accurate results.
-
Finance and Accounting: In financial modeling or accounting, this fraction might represent a small portion of a budget or a share in a company. Understanding proportions is fundamental in financial calculations and analysis.
-
Data Analysis: In data analysis, fractions can represent the proportion of a certain outcome or characteristic within a dataset. For instance, 1/48 could represent the percentage of respondents who chose a specific answer in a survey.
Decimal and Percentage Equivalents of 1/48
Converting a fraction to its decimal and percentage equivalents helps in understanding its magnitude more intuitively.
To convert 1/48 to a decimal, we divide the numerator (1) by the denominator (48):
1 ÷ 48 ≈ 0.020833
To convert the decimal to a percentage, we multiply by 100:
0.020833 x 100 ≈ 2.0833%
Therefore, 1/48 is approximately equal to 0.020833 or 2.0833%.
Beyond the Basics: Expanding Mathematical Understanding
Understanding fractions like 10/480 and its simplified form 1/48 goes beyond simple arithmetic. It builds a strong foundation for more advanced mathematical concepts:
-
Ratios and Proportions: Fractions are fundamental to understanding ratios and proportions. A ratio compares two quantities, and a proportion states that two ratios are equal. This is crucial in various fields, including geometry, physics, and chemistry.
-
Algebra and Equations: Fractions are integral to solving algebraic equations and inequalities. Understanding fraction operations is essential for manipulating equations and finding solutions.
-
Calculus: Calculus involves working with limits, derivatives, and integrals. A solid understanding of fractions is crucial for understanding these concepts and performing related calculations.
Frequently Asked Questions (FAQ)
Q1: Why is simplifying fractions important?
A1: Simplifying fractions makes them easier to understand, compare, and work with. It reduces computational complexity and enhances clarity in calculations.
Q2: Are there other methods to find the GCD besides prime factorization?
A2: Yes, the Euclidean algorithm is another efficient method to find the GCD of two numbers.
Q3: Can I use a calculator to simplify fractions?
A3: Many calculators have built-in functions to simplify fractions. However, understanding the process manually is crucial for grasping the underlying mathematical concepts.
Q4: What if the numerator and denominator have no common factors?
A4: If the numerator and denominator have no common factors other than 1, then the fraction is already in its simplest form.
Conclusion: The Significance of Simple Fractions
While the fraction 10/480 might seem trivial at first glance, a closer examination reveals its mathematical richness and practical significance. Understanding its simplification to 1/48, its equivalent forms, and its applications across various fields showcases the importance of mastering fundamental mathematical concepts. This seemingly simple fraction serves as a building block for more advanced mathematical understanding, highlighting the significance of attention to detail and the power of simplification in revealing the essence of mathematical relationships. By mastering the art of simplifying fractions, we build a strong foundation for tackling complex problems across diverse disciplines. The journey from 10/480 to 1/48 demonstrates not only a mathematical process but also a valuable lesson in precision, accuracy, and the beauty of mathematical simplicity.
Latest Posts
Latest Posts
-
70 Of 7
Sep 13, 2025
-
Crown At Hallow
Sep 13, 2025
-
3 3kg In Lbs
Sep 13, 2025
-
Poacher Turned Gamekeeper
Sep 13, 2025
-
7 5 To Fraction
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 10 Of 480 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.