3 X -3
stanleys
Sep 12, 2025 · 5 min read
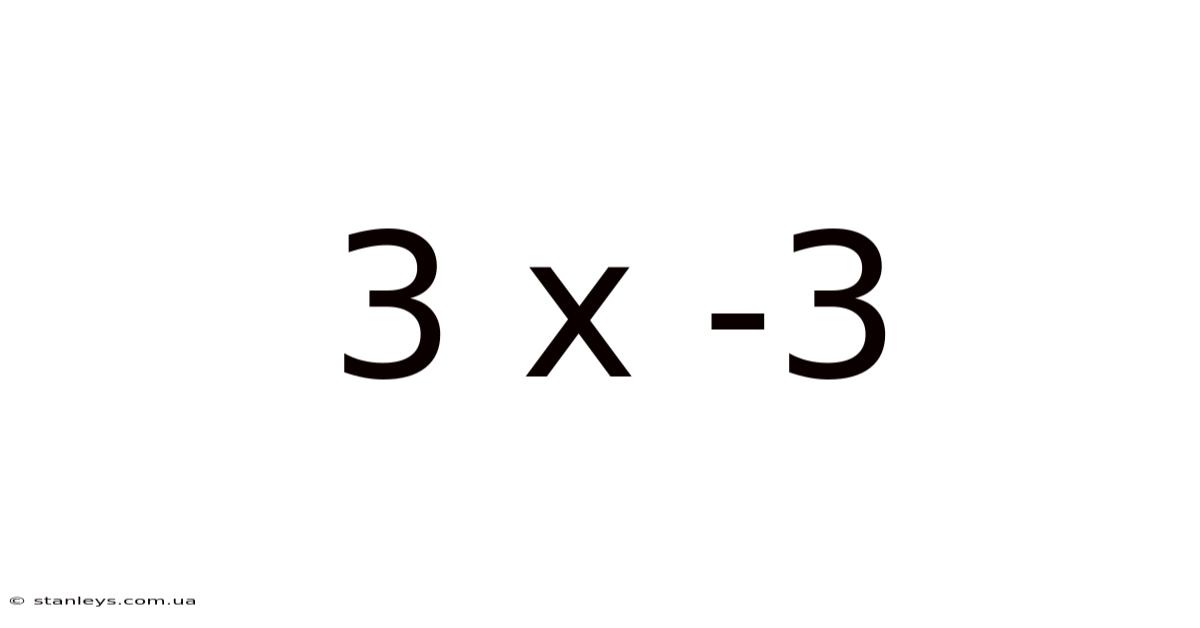
Table of Contents
Decoding 3x - 3: A Deep Dive into Algebraic Expressions
This article explores the seemingly simple algebraic expression, 3x - 3, unraveling its components, applications, and broader implications within the world of mathematics. We'll move beyond simply evaluating the expression for specific values of 'x' to understand its underlying structure, its graphical representation, and its significance in problem-solving. This comprehensive guide is designed for students and anyone looking to strengthen their foundational understanding of algebra. We'll cover everything from basic simplification to more advanced concepts related to this fundamental expression.
Introduction: Understanding the Building Blocks
The expression 3x - 3 is a fundamental example of an algebraic expression. It combines numbers (constants), variables (represented by 'x'), and mathematical operations (multiplication and subtraction). Let's break down each component:
-
3: This is a constant. It represents a fixed numerical value that doesn't change.
-
x: This is a variable. It represents an unknown quantity or a placeholder for a value that can change.
-
3x: This represents the product of 3 and x. In other words, 3 is multiplied by the value of x.
-
-: This is the subtraction operator, indicating that we're subtracting 3 from the product 3x.
Simplifying the Expression: Factoring
While 3x - 3 is already a relatively simple expression, we can further simplify it through a process called factoring. Factoring involves finding common factors among the terms and expressing the expression as a product of these factors. In this case, both 3x and -3 share a common factor of 3. Therefore, we can factor out the 3:
3x - 3 = 3(x - 1)
This factored form is equally valid and often more useful in certain contexts, such as solving equations or understanding the expression's graphical representation.
Evaluating the Expression: Finding Numerical Values
To find the numerical value of 3x - 3, we need to substitute a specific value for the variable 'x'. For example:
- If x = 0: 3(0) - 3 = -3
- If x = 1: 3(1) - 3 = 0
- If x = 2: 3(2) - 3 = 3
- If x = -1: 3(-1) - 3 = -6
- If x = 5: 3(5) - 3 = 12
These examples demonstrate how the value of the expression changes based on the value assigned to x. This is a fundamental concept in algebra: the variable allows the expression to represent a range of possible values.
Graphical Representation: Visualizing the Expression
The expression 3x - 3 can be graphically represented as a straight line on a Cartesian coordinate system. This line has a slope of 3 and a y-intercept of -3.
-
Slope: The slope represents the rate of change of the expression. In this case, a slope of 3 means that for every one-unit increase in x, the value of the expression increases by 3 units.
-
Y-intercept: The y-intercept is the point where the line intersects the y-axis (where x = 0). In this case, the y-intercept is -3, which corresponds to the value of the expression when x = 0.
Understanding the graphical representation helps to visualize the relationship between x and the value of the expression. It allows us to quickly estimate the value of the expression for different values of x and to observe its overall behavior.
Solving Equations: Applying the Expression
The expression 3x - 3 often appears in equations. For instance, consider the equation:
3x - 3 = 6
To solve for x, we use algebraic manipulation:
- Add 3 to both sides: 3x = 9
- Divide both sides by 3: x = 3
Therefore, the solution to the equation 3x - 3 = 6 is x = 3. This process highlights how the expression 3x - 3 plays a role in solving more complex mathematical problems.
Applications in Real-World Scenarios
While seemingly abstract, the expression 3x - 3 has practical applications in various real-world scenarios. Consider these examples:
-
Cost Calculations: Imagine you're buying items that cost $3 each, and there's a $3 shipping fee. The total cost (C) can be expressed as C = 3x - 3, where x represents the number of items bought. If you buy 5 items, the total cost would be 3(5) - 3 = $12.
-
Linear Relationships: Many real-world relationships can be modeled using linear equations, which often involve expressions similar to 3x - 3. For example, the relationship between distance and time for a moving object at a constant speed can be represented by a linear equation.
-
Profit Calculations: Imagine a business with a fixed cost of $3 and a profit of $3 per unit sold. The profit (P) can be represented by P = 3x - 3, where x represents the number of units sold.
Advanced Concepts and Extensions
The expression 3x - 3 serves as a foundation for understanding more complex algebraic concepts:
-
Functions: The expression can be considered a simple linear function, where the output (the value of the expression) depends on the input (the value of x). This concept is central to calculus and other advanced mathematical fields.
-
Inequalities: Instead of an equation, we can use the expression in inequalities, such as 3x - 3 > 0. Solving this inequality involves finding the range of x values that satisfy the condition.
-
Systems of Equations: The expression might be part of a system of equations, requiring us to solve for multiple variables simultaneously.
Frequently Asked Questions (FAQ)
-
Q: What is the difference between 3x and 3 + x?
- A: 3x means 3 multiplied by x, whereas 3 + x means 3 added to x. These are fundamentally different operations leading to different results.
-
Q: Can we simplify 3x - 3 any further than 3(x - 1)?
- A: Without knowing the value of x, 3(x - 1) is the simplest factored form.
-
Q: What if x is a negative number?
- A: The expression still holds true. Just remember to follow the rules of arithmetic with negative numbers. For example, if x = -2, then 3x - 3 = 3(-2) - 3 = -9.
Conclusion: The Power of Simplicity
While seemingly simple, the algebraic expression 3x - 3 embodies fundamental concepts in algebra, providing a building block for understanding more complex mathematical ideas. Its simplicity belies its power and versatility, making it a crucial element in various mathematical applications and real-world problem-solving. Through this exploration, we've moved beyond simple evaluation to gain a deeper appreciation for its structure, graphical representation, and its significance in solving equations and modeling real-world phenomena. Mastering this fundamental expression lays a strong foundation for tackling more advanced algebraic challenges.
Latest Posts
Latest Posts
-
3 12 Simplified
Sep 12, 2025
-
Tree Is Spanish
Sep 12, 2025
-
40 Of 16
Sep 12, 2025
-
Symbols Of Aztecs
Sep 12, 2025
-
62 1kg To Stone
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 3 X -3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.