3 12 Simplified
stanleys
Sep 12, 2025 · 6 min read
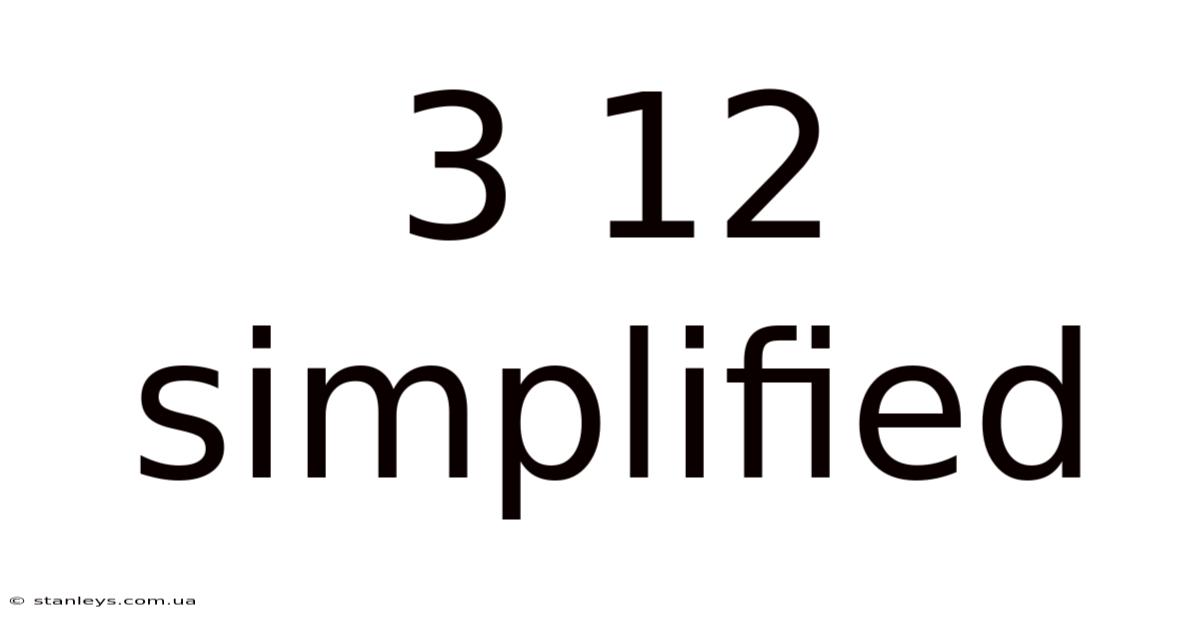
Table of Contents
3/12 Simplified: Understanding and Mastering the Concept
Understanding fractions can be a hurdle for many, but mastering them opens doors to more advanced mathematical concepts. This article delves into the simplification of the fraction 3/12, explaining the process in detail and providing a broader understanding of fraction reduction. We'll explore the underlying principles, practical examples, and answer frequently asked questions to solidify your grasp of this fundamental mathematical skill.
Introduction: What is Fraction Simplification?
Fraction simplification, also known as reducing fractions or expressing fractions in their simplest form, is the process of finding an equivalent fraction with smaller numbers. This doesn't change the fraction's value; it merely represents it in a more concise and manageable way. The fraction 3/12, for instance, can be simplified to a smaller, equivalent fraction. This simplification makes calculations easier and improves understanding of the fraction's magnitude. Understanding this process is crucial for further progress in mathematics, particularly in algebra and calculus.
Understanding the Concept of Equivalent Fractions
Before we dive into simplifying 3/12, let's establish the core concept of equivalent fractions. Equivalent fractions represent the same portion or value, even though they have different numerators and denominators. For example, 1/2, 2/4, 3/6, and 4/8 are all equivalent fractions because they all represent one-half. The key to finding equivalent fractions lies in multiplying or dividing both the numerator and the denominator by the same non-zero number.
Simplifying 3/12: A Step-by-Step Approach
The simplification of 3/12 involves finding the greatest common divisor (GCD) of the numerator (3) and the denominator (12). The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder.
-
Find the GCD of 3 and 12:
To find the GCD, we can list the factors of each number:
- Factors of 3: 1, 3
- Factors of 12: 1, 2, 3, 4, 6, 12
The largest number that appears in both lists is 3. Therefore, the GCD of 3 and 12 is 3.
-
Divide both the numerator and the denominator by the GCD:
Now, we divide both the numerator (3) and the denominator (12) by the GCD (3):
- 3 ÷ 3 = 1
- 12 ÷ 3 = 4
-
The Simplified Fraction:
This gives us the simplified fraction 1/4. Therefore, 3/12 is equivalent to 1/4. They represent the same portion or value.
Visual Representation of 3/12 and 1/4
Imagine a pizza cut into 12 slices. 3/12 represents 3 out of those 12 slices. Now imagine a smaller pizza cut into 4 slices. 1/4 represents 1 out of those 4 slices. If you consume 3 slices of the first pizza and 1 slice of the second pizza, you've consumed the same amount. This visually demonstrates the equivalence of 3/12 and 1/4.
Alternative Methods for Finding the GCD
While listing factors is a straightforward method for small numbers, it becomes less efficient for larger numbers. Here are two alternative methods for finding the GCD:
-
Prime Factorization: This method involves breaking down each number into its prime factors. The GCD is the product of the common prime factors raised to the lowest power.
- Prime factorization of 3: 3
- Prime factorization of 12: 2 x 2 x 3 = 2² x 3
The common prime factor is 3, and its lowest power is 3¹. Therefore, the GCD is 3.
-
Euclidean Algorithm: This is a more efficient algorithm for finding the GCD of larger numbers. It involves repeatedly applying the division algorithm until the remainder is 0. The last non-zero remainder is the GCD.
- Divide 12 by 3: 12 = 3 x 4 + 0
- Since the remainder is 0, the GCD is the divisor, which is 3.
Practical Applications of Fraction Simplification
Simplifying fractions is not just a theoretical exercise; it has numerous practical applications in various fields:
-
Cooking and Baking: Recipes often require fractional measurements. Simplifying fractions makes it easier to understand and measure ingredients accurately.
-
Construction and Engineering: Precise measurements are critical in construction and engineering. Simplifying fractions ensures accuracy in calculations and designs.
-
Finance: Understanding fractions is essential in managing finances, calculating percentages, and dealing with interest rates.
-
Data Analysis: Data analysis often involves dealing with fractions and proportions. Simplifying fractions helps in presenting data clearly and efficiently.
-
Everyday Life: We encounter fractions in various aspects of daily life, from sharing things equally to understanding sales discounts.
Beyond 3/12: Simplifying Other Fractions
The process of simplifying fractions, as illustrated with 3/12, applies to all fractions. The key is always to find the greatest common divisor of the numerator and the denominator and then divide both by that GCD. For example:
-
Simplifying 6/18: The GCD of 6 and 18 is 6. Dividing both by 6 gives 1/3.
-
Simplifying 15/25: The GCD of 15 and 25 is 5. Dividing both by 5 gives 3/5.
-
Simplifying 24/36: The GCD of 24 and 36 is 12. Dividing both by 12 gives 2/3.
Common Mistakes to Avoid When Simplifying Fractions
-
Dividing only the numerator or denominator: Remember, you must divide both the numerator and the denominator by the GCD.
-
Using an incorrect GCD: Ensure you accurately identify the greatest common divisor. Using a smaller common divisor will result in a fraction that is not fully simplified.
-
Not simplifying completely: Always check if the simplified fraction can be further reduced.
Frequently Asked Questions (FAQ)
Q: What if the numerator and denominator have no common factors other than 1?
A: If the GCD is 1, the fraction is already in its simplest form. It cannot be simplified further. Such fractions are called irreducible fractions.
Q: Can I simplify a fraction by multiplying the numerator and denominator by the same number?
A: No, multiplying both by the same number creates an equivalent fraction, but it doesn't simplify it; it makes the numbers larger. Simplification involves reducing the numbers.
Q: Is there a shortcut to simplify fractions quickly?
A: For smaller fractions, you can often spot the GCD easily. For larger numbers, using prime factorization or the Euclidean algorithm is more efficient.
Q: Why is simplifying fractions important?
A: Simplification makes fractions easier to understand, compare, and use in calculations. It also ensures consistency and clarity in presenting mathematical results.
Conclusion: Mastering Fraction Simplification
Mastering the simplification of fractions like 3/12 is fundamental to success in mathematics. By understanding the concept of equivalent fractions, finding the greatest common divisor, and consistently applying the division process, you can confidently simplify any fraction. Remember to practice regularly to build fluency and accuracy. This skill will not only help you excel in your math studies but also enhance your problem-solving abilities in various real-world scenarios. Don't hesitate to review the steps and examples provided in this article to solidify your understanding and confidently tackle any fraction simplification challenges you may encounter.
Latest Posts
Latest Posts
-
20 Of 28
Sep 12, 2025
-
3 2 Km Miles
Sep 12, 2025
-
Mmhg En Pa
Sep 12, 2025
-
2 Of 300
Sep 12, 2025
-
10 Of 125
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 3 12 Simplified . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.