25 Of 35000
stanleys
Sep 17, 2025 · 6 min read
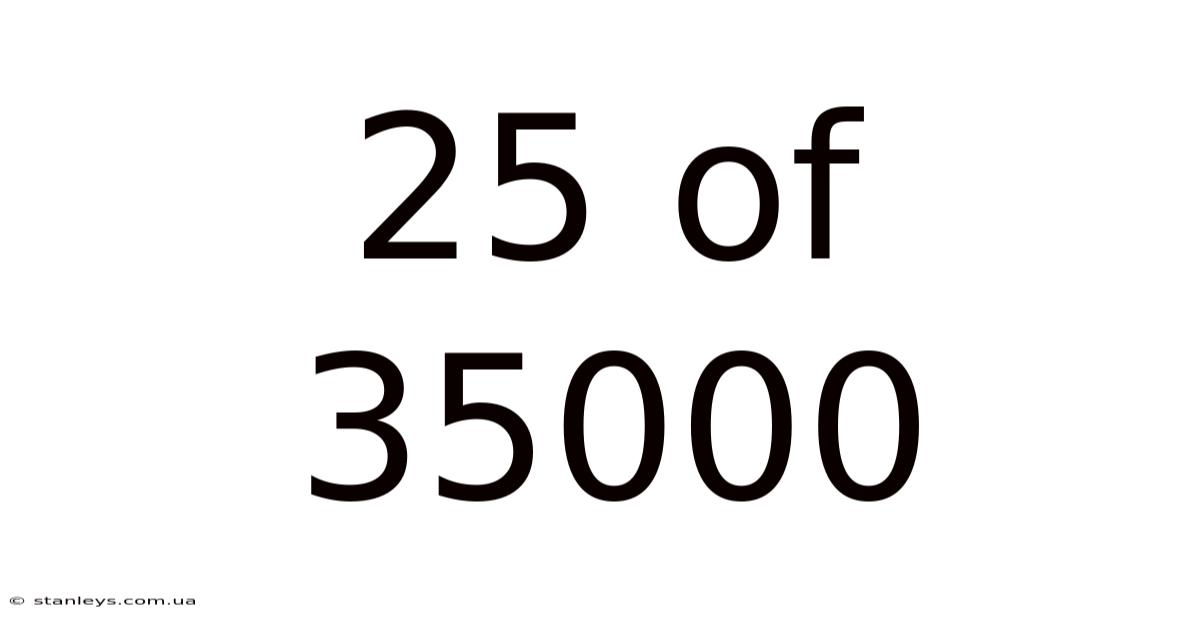
Table of Contents
Unveiling the Significance of 25 out of 35,000: A Deep Dive into Statistical Significance, Probability, and Real-World Applications
The seemingly small fraction of 25 out of 35,000 might appear insignificant at first glance. However, depending on the context, this ratio can hold profound implications. This article delves into the meaning and significance of this numerical relationship, exploring its statistical implications, calculating probabilities, and examining real-world applications where such a ratio might carry considerable weight. We'll move beyond a simple percentage and explore the underlying principles that determine the importance of this figure.
Understanding the Context: The Importance of Background Information
Before we delve into calculations, it's crucial to understand that the significance of "25 out of 35,000" entirely depends on the context. This ratio could represent anything from the number of defective products in a batch to the number of successful clinical trial participants. Without knowing the specific context, any statistical analysis would be incomplete and potentially misleading. Let's imagine several scenarios:
-
Scenario 1: Defective Products: If 25 out of 35,000 manufactured widgets are defective, this represents a defect rate of approximately 0.07%. This might be acceptable depending on industry standards and the cost of remediation.
-
Scenario 2: Clinical Trial Success: If 25 out of 35,000 participants in a clinical trial experienced a complete remission of a serious illness, this could represent a significant breakthrough, warranting further investigation and potentially a change in treatment protocols. The success rate here is also around 0.07%, but the impact is vastly different due to the nature of the context.
-
Scenario 3: Lottery Winners: If 25 people out of 35,000 lottery ticket holders won a significant prize, this might be considered a surprisingly high number of winners, prompting an investigation into the fairness of the lottery.
Calculating Probabilities and Statistical Significance
To analyze the significance of 25 out of 35,000, we can employ several statistical approaches:
-
Percentage Calculation: The simplest approach is to calculate the percentage: (25/35000) * 100% ≈ 0.07%. This gives us a basic understanding of the proportion. However, a simple percentage alone doesn't tell the whole story. The statistical significance depends on several factors, including the expected rate and the variability inherent in the system.
-
Binomial Probability: If we assume the events (e.g., defective products, successful treatments) are independent and the probability of success (or failure) is constant, we can use the binomial probability distribution to calculate the probability of observing 25 successes (or failures) in 35,000 trials. This calculation requires knowing the underlying probability of success (or failure). Without this prior knowledge, we can only estimate.
-
Hypothesis Testing: In many scenarios, particularly in scientific research, hypothesis testing is employed. We might formulate a null hypothesis (e.g., the treatment has no effect, the defect rate is 0.1%) and then use statistical tests like the z-test or chi-squared test to determine whether the observed data (25 successes out of 35,000) provides enough evidence to reject the null hypothesis in favor of an alternative hypothesis. The p-value obtained from this test indicates the probability of observing the data if the null hypothesis were true. A small p-value (typically below 0.05) suggests that the null hypothesis should be rejected. This is where statistical significance is determined.
Exploring Real-World Applications
The ratio of 25 out of 35,000 finds applications in diverse fields:
-
Manufacturing and Quality Control: As mentioned earlier, identifying a small percentage of defective products is vital for maintaining quality standards. Statistical process control techniques use data like this to monitor production processes and identify potential issues before they escalate.
-
Medicine and Clinical Trials: In clinical trials, evaluating the efficacy of a new drug or treatment often involves comparing success rates between treatment and control groups. A statistically significant difference in success rates can determine whether a new treatment is effective. Determining if 25 out of 35,000 is statistically significant would depend heavily on the control group's success rate.
-
Environmental Science: Analyzing environmental data, such as the number of endangered species in a population, often involves ratios similar to 25 out of 35,000. These figures are crucial for understanding the health of ecosystems and guiding conservation efforts.
-
Social Sciences and Surveys: Large-scale surveys often involve analyzing responses from thousands of participants. A small subset of respondents exhibiting a particular trait or opinion, such as 25 out of 35,000 expressing strong disapproval, could indicate an underlying trend.
-
Finance and Risk Management: In finance, analyzing a small number of defaults out of a large portfolio of loans helps assess risk and inform investment strategies.
Understanding the Limitations and Importance of Further Analysis
It’s vital to emphasize that simply knowing the ratio of 25 out of 35,000 doesn’t provide a complete picture. Several other factors are critical:
-
Underlying Probability: What was the expected rate? If the expected defect rate was 0.1%, then 25 out of 35,000 might be considered low. However, if the expected rate was much lower, this could signify a problem.
-
Confidence Intervals: Calculating confidence intervals around the observed proportion helps quantify the uncertainty associated with the estimate. This helps us understand the range of plausible values for the true proportion.
-
Sampling Methods: The way the data was collected significantly affects its reliability. A biased sample can lead to misleading results.
-
Statistical Power: The power of a statistical test refers to its ability to detect a real effect if one exists. Low power can lead to false negatives, where a true difference isn't detected.
Frequently Asked Questions (FAQ)
-
Q: Is 25 out of 35,000 a statistically significant number? A: This depends entirely on the context and the statistical test used. Without knowing the background, this question cannot be answered.
-
Q: What statistical tests can I use to analyze this data? A: Depending on the nature of the data, appropriate tests include z-tests, chi-squared tests, binomial tests, and others. The choice depends on the type of data and the research question.
-
Q: How can I calculate the confidence interval for this ratio? A: There are several methods to calculate confidence intervals for proportions, including using the normal approximation or exact methods. Statistical software packages can easily perform this calculation.
-
Q: What if the events are not independent? A: If the events are not independent (e.g., the occurrence of one event influences the likelihood of another), then the binomial distribution may not be appropriate. More advanced statistical models would be needed to analyze the data accurately.
Conclusion: The Importance of Context and Further Investigation
The ratio of 25 out of 35,000 is only a starting point for analysis. Its significance is entirely context-dependent. While a simple percentage calculation provides a basic understanding, a more thorough statistical analysis, including hypothesis testing and confidence interval calculation, is crucial for drawing meaningful conclusions. The specific methodology employed depends heavily on the underlying research question, the nature of the data, and any prior assumptions or knowledge about the system. Always remember that context is king, and thorough statistical analysis is essential for interpreting data accurately and avoiding misleading conclusions. The seemingly insignificant number can, in the right context, reveal profound insights.
Latest Posts
Latest Posts
-
100 X 2
Sep 18, 2025
-
77f To C
Sep 18, 2025
-
5 0 X 10
Sep 18, 2025
-
30 Of 400
Sep 18, 2025
-
180g To Kg
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 25 Of 35000 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.