5.0 X 10
stanleys
Sep 18, 2025 · 7 min read
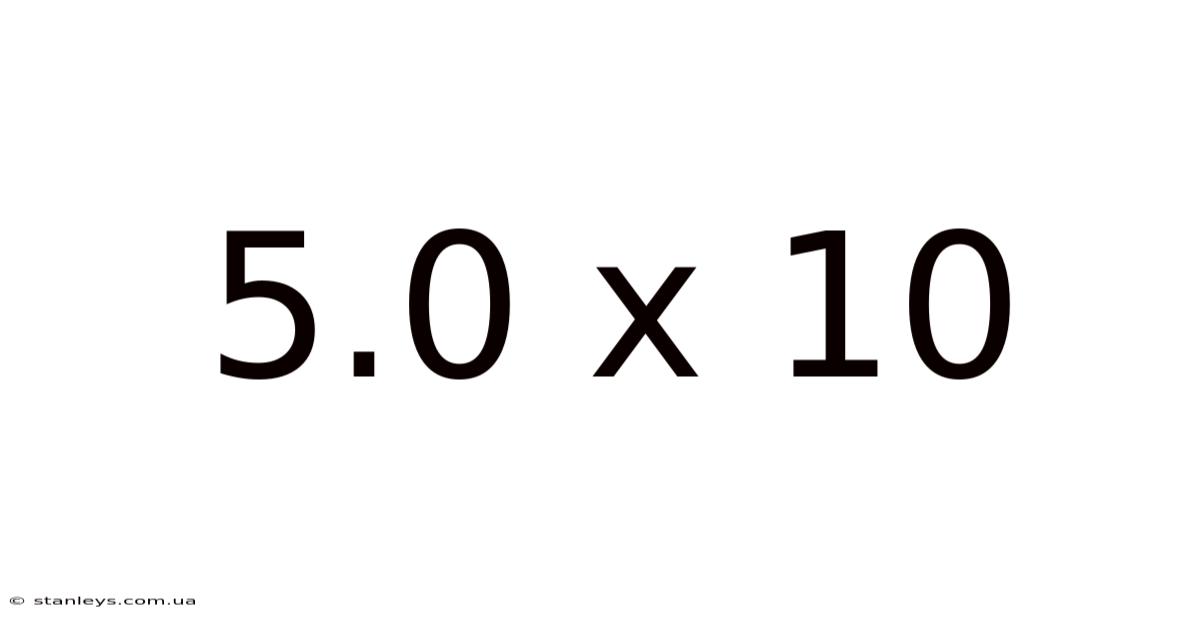
Table of Contents
Decoding 5.0 x 10: Exploring Scientific Notation and its Applications
Scientific notation, a cornerstone of scientific communication, provides a concise way to represent extremely large or small numbers. Understanding 5.0 x 10, a relatively simple example, unlocks the broader understanding of this powerful tool used across various scientific disciplines. This article will delve into the meaning of 5.0 x 10, explain the principles of scientific notation, explore its applications, and address frequently asked questions. We'll unravel the mystery of this seemingly simple expression and show you how it fits into the larger context of scientific calculations and data representation.
Understanding Scientific Notation: A Foundation
Scientific notation is a standardized way of writing numbers that are either very large or very small. It's based on expressing numbers as a product of a coefficient and a power of 10. The general form is:
a x 10<sup>b</sup>
Where:
- a is the coefficient, a number between 1 and 10 (but not including 10).
- b is the exponent, an integer representing the power of 10.
This system makes handling extremely large or small numbers far more manageable than writing out all the zeros. For instance, the distance to the sun (approximately 149,600,000,000 meters) is much easier to express in scientific notation as 1.496 x 10<sup>11</sup> meters.
Deconstructing 5.0 x 10
Now, let's focus on 5.0 x 10. At first glance, this might seem trivial because it doesn't represent an extremely large or small number. However, it serves as an excellent starting point to grasp the fundamental principles.
In this case:
- a = 5.0 This is our coefficient, a number between 1 and 10.
- b = 1 This is our exponent. It indicates that we're multiplying the coefficient by 10 raised to the power of 1.
Therefore, 5.0 x 10<sup>1</sup> is equivalent to 5.0 x 10 = 50.
While this particular example doesn't showcase the dramatic simplification seen with extremely large numbers, it illustrates the core concept. The power of 10 dictates how many places the decimal point moves. A positive exponent shifts the decimal point to the right, while a negative exponent shifts it to the left.
Applications of Scientific Notation Across Disciplines
Scientific notation transcends simple mathematical exercises; it's a vital tool in numerous fields:
-
Astronomy: Dealing with vast distances, like those between stars and galaxies, necessitates scientific notation. The distances involved are so immense that expressing them in standard form would be impractical.
-
Chemistry: In chemistry, we frequently encounter incredibly small numbers, such as the mass of atoms and molecules. Scientific notation elegantly handles these minuscule values. For example, the mass of a single hydrogen atom is approximately 1.67 x 10<sup>-27</sup> kg.
-
Physics: From subatomic particles to the scale of the universe, physics deals with a vast range of magnitudes. Scientific notation simplifies calculations and data representation across all these scales.
-
Computer Science: Computers often work with very large or very small numbers, particularly in data processing and simulations. Scientific notation helps manage the data efficiently.
-
Engineering: Engineers use scientific notation in various calculations, including those related to material properties, signal processing, and structural analysis.
-
Biology: In biology, the number of cells in an organism, the concentration of certain molecules, or the scale of microbial populations often requires scientific notation for practical representation and calculations.
-
Finance: Though less frequent than in the hard sciences, scientific notation can prove useful when dealing with extremely large sums of money, especially in international finance or analyses of global economic trends.
Converting Between Standard and Scientific Notation
The ability to easily convert between standard notation (the way we usually write numbers) and scientific notation is essential.
Converting from Standard to Scientific Notation:
- Move the decimal point to the left or right until you have a number between 1 and 10.
- Count the number of places you moved the decimal point. This number becomes the exponent.
- If you moved the decimal point to the left, the exponent is positive.
- If you moved the decimal point to the right, the exponent is negative.
Example: Convert 2,500,000 to scientific notation.
- Move the decimal point six places to the left: 2.5
- The exponent is 6 (positive because we moved the decimal to the left).
- The scientific notation is 2.5 x 10<sup>6</sup>.
Converting from Scientific Notation to Standard Notation:
- Identify the exponent.
- Move the decimal point the number of places indicated by the exponent.
- Move the decimal point to the right if the exponent is positive.
- Move the decimal point to the left if the exponent is negative. Add zeros as needed.
Example: Convert 1.2 x 10<sup>-3</sup> to standard notation.
- The exponent is -3.
- Move the decimal point three places to the left: 0.0012
Advanced Concepts and Considerations
While 5.0 x 10 is a simple example, mastering scientific notation requires understanding more advanced concepts:
-
Significant Figures: Scientific notation often involves significant figures, which represent the precision of a measurement. The number of significant figures dictates how many digits are considered reliable.
-
Operations with Scientific Notation: Performing calculations (addition, subtraction, multiplication, and division) with numbers in scientific notation requires specific rules to simplify the process and maintain accuracy.
-
Unit Conversions: Scientific notation is frequently used in conjunction with unit conversions to simplify calculations and ensure consistency in measurements.
-
Logarithms: Logarithms are closely related to scientific notation, often used to simplify calculations involving extremely large or small numbers. Understanding logarithms enhances the application of scientific notation.
-
Error Propagation: When performing calculations with numbers expressed in scientific notation, understanding how uncertainties (errors) propagate through the calculations is critical for maintaining the accuracy and reliability of results.
Frequently Asked Questions (FAQ)
Q: Why is scientific notation important?
A: Scientific notation provides a concise and efficient way to represent extremely large or small numbers, simplifying calculations and improving data management across various scientific disciplines.
Q: Can I use scientific notation for numbers that aren't very large or small?
A: Yes, you can. While it's particularly useful for extreme values, it can be applied to any number to maintain consistency and clarity in scientific and engineering contexts.
Q: What if the coefficient is not between 1 and 10?
A: If your coefficient is not between 1 and 10, you need to adjust the exponent accordingly to bring it within that range.
Q: How do I perform calculations (addition, subtraction, multiplication, and division) with numbers in scientific notation?
A: Specific rules govern calculations with scientific notation. For multiplication and division, you multiply or divide the coefficients and add or subtract the exponents, respectively. For addition and subtraction, you must ensure that the numbers have the same exponent before performing the operation.
Q: Are there any limitations to using scientific notation?
A: While powerful, scientific notation might not be the most intuitive for individuals unfamiliar with the concept. Additionally, it doesn't directly convey the physical magnitude of extremely large or small quantities as effectively as visual representations or analogies.
Conclusion
5.0 x 10, seemingly a simple expression, serves as a gateway to understanding the broader implications of scientific notation. From astronomy to biology, this system is fundamental to communicating and manipulating a vast range of numerical values. Mastering scientific notation is not just about memorizing rules; it's about developing a deeper appreciation for the elegance and efficiency of this crucial tool in scientific communication and analysis. By grasping its fundamental principles and exploring its applications across different scientific fields, you gain a powerful skillset applicable to various areas of study and research. Its value lies not only in simplifying complex calculations but also in fostering a more profound understanding of the scale and scope of phenomena in our universe.
Latest Posts
Latest Posts
-
3x 1 7
Sep 18, 2025
-
Red On Orange
Sep 18, 2025
-
Protein Rib Eye
Sep 18, 2025
-
95lbs In Kg
Sep 18, 2025
-
3 0 5
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 5.0 X 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.