100 X 2
stanleys
Sep 18, 2025 · 5 min read
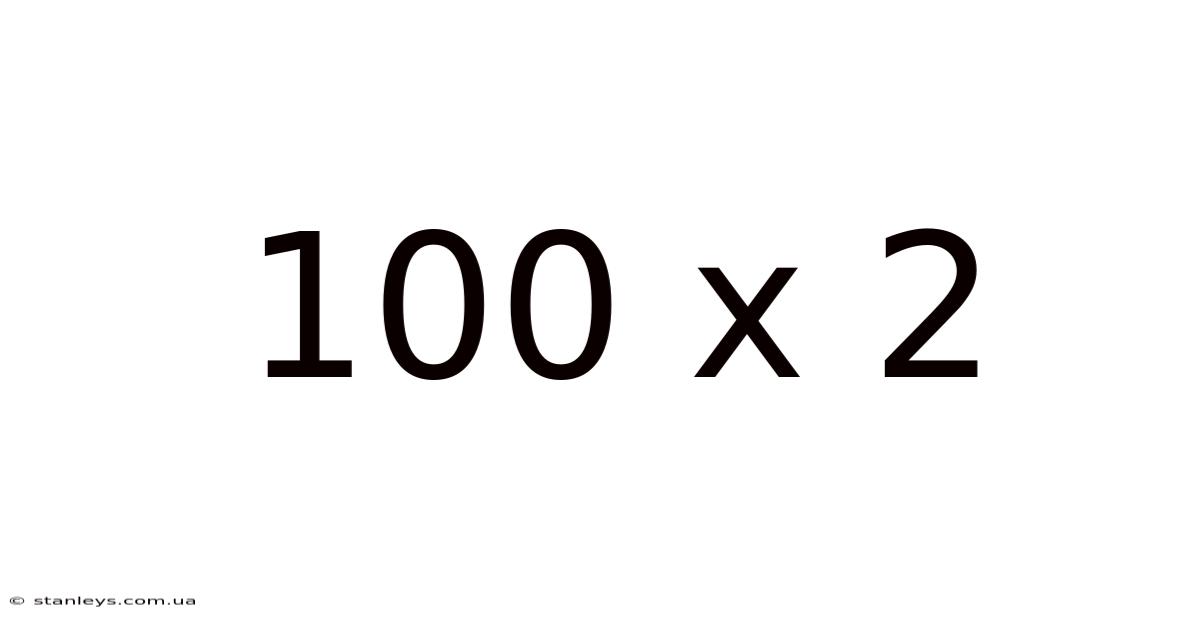
Table of Contents
Unpacking 100 x 2: A Deep Dive into Multiplication, Its Applications, and Beyond
This article explores the seemingly simple equation, 100 x 2, going far beyond the immediate answer of 200. We'll delve into the fundamental concepts of multiplication, explore its real-world applications, examine different approaches to solving the problem, and even touch upon the broader mathematical principles it represents. This will be a journey from basic arithmetic to a deeper appreciation of mathematical thinking. Understanding 100 x 2 is a stepping stone to grasping more complex mathematical concepts.
Understanding Multiplication: The Basics
At its core, multiplication is repeated addition. When we say 100 x 2, we are essentially asking: what is the sum of 100 added to itself two times? (100 + 100 = 200). This simple interpretation is crucial for understanding the underlying logic of multiplication, especially when dealing with larger numbers or more complex scenarios. The number 100 is the multiplicand (the number being multiplied), and 2 is the multiplier (the number indicating how many times the multiplicand is added to itself). The result, 200, is the product.
Different Ways to Solve 100 x 2
While the answer is straightforward, let's explore diverse methods to calculate 100 x 2, highlighting different mathematical approaches:
-
Repeated Addition: As mentioned earlier, this is the most fundamental method. Simply add 100 to itself twice: 100 + 100 = 200. This method is useful for visualizing the concept of multiplication, particularly for younger learners.
-
Using the Distributive Property: The distributive property states that a(b + c) = ab + ac. While seemingly unnecessary for 100 x 2, this property becomes invaluable when dealing with more complex calculations. We could break down 100 into smaller parts (e.g., 50 + 50) and apply the distributive property: 2(50 + 50) = 2(50) + 2(50) = 100 + 100 = 200.
-
Mental Math: With practice, many people can quickly calculate 100 x 2 mentally. This involves recognizing that multiplying by 2 is equivalent to doubling the number. Doubling 100 is easily visualized as adding a zero to 100, resulting in 200.
-
Using a Calculator: While not as conceptually enriching, a calculator provides a quick and efficient way to calculate 100 x 2, particularly for large or complex calculations where mental math may become challenging.
Real-World Applications of 100 x 2 and Multiplication in General
The seemingly simple equation 100 x 2 has numerous real-world applications. Consider these examples:
-
Shopping: If you buy two items that cost $100 each, the total cost will be 100 x 2 = $200.
-
Measurement: If a room is 100 centimeters wide and you need to double its width, the new width will be 100 x 2 = 200 centimeters.
-
Cooking: If a recipe calls for 100 grams of flour and you want to double the recipe, you'll need 100 x 2 = 200 grams of flour.
-
Finance: If you invest $100 and your investment doubles in value, you'll have 100 x 2 = $200.
These examples highlight the pervasive nature of multiplication in everyday life. It's fundamental to various fields, including:
-
Engineering: Calculating dimensions, forces, and material quantities.
-
Finance: Calculating interest, profit, and loss.
-
Computer Science: Performing calculations and processing data.
-
Physics: Solving equations related to motion, energy, and forces.
Expanding the Concept: Beyond 100 x 2
While 100 x 2 provides a concrete example, let's broaden our perspective to understand the broader implications:
-
Scaling and Proportion: Multiplication is crucial for understanding scaling and proportion. If a map has a scale of 1:100, then 2 centimeters on the map represent 2 x 100 = 200 centimeters in reality. This principle extends to various fields, including architecture, cartography, and engineering.
-
Algebraic Expressions: The concept of multiplication extends seamlessly to algebra. Instead of specific numbers, we use variables (e.g., x, y, z) which represent unknown quantities. The expression 100x represents the product of 100 and an unknown value x. This ability to generalize numerical operations is a cornerstone of algebra and higher mathematics.
-
Geometric Applications: Multiplication is integral to calculating areas and volumes. The area of a rectangle is calculated by multiplying its length and width. Similarly, the volume of a rectangular prism is found by multiplying its length, width, and height.
-
Number Theory: Multiplication plays a fundamental role in number theory, a branch of mathematics focused on the properties of integers. Concepts like prime factorization, divisibility rules, and modular arithmetic rely heavily on multiplication.
Frequently Asked Questions (FAQ)
Q: What is the quickest way to calculate 100 x 2?
A: The quickest method is likely mental math, recognizing that multiplying by 2 is the same as doubling the number. Simply doubling 100 gives you 200.
Q: Is there any other way to express 100 x 2?
A: Yes, you could express it as 2 x 100 (the commutative property of multiplication states that the order of the operands does not affect the result), or as 100 + 100 (representing repeated addition).
Q: Why is multiplication important?
A: Multiplication is crucial because it provides an efficient way to perform repeated addition, enabling us to solve problems quickly and efficiently across numerous fields, from everyday tasks to complex scientific calculations. It's a fundamental building block for many advanced mathematical concepts.
Q: How does multiplication relate to division?
A: Multiplication and division are inverse operations. Just as 100 x 2 = 200, 200 / 2 = 100 and 200 / 100 = 2. They represent opposite actions, allowing us to solve for unknown quantities in various mathematical problems.
Conclusion: The Significance of Simple Multiplication
While seemingly elementary, understanding 100 x 2 opens doors to a wealth of mathematical concepts and real-world applications. This seemingly simple equation serves as a foundation for grasping more complex calculations, algebraic expressions, geometric principles, and broader mathematical theories. The journey from understanding basic multiplication to appreciating its diverse applications underscores the importance of a strong mathematical foundation in navigating various aspects of life and advanced studies. The ability to understand and apply simple arithmetic operations like multiplication is not just a mathematical skill but a vital tool for problem-solving and critical thinking in numerous contexts.
Latest Posts
Latest Posts
-
3000g To Lbs
Sep 18, 2025
-
Low Cost Wigs
Sep 18, 2025
-
3x 1 7
Sep 18, 2025
-
Red On Orange
Sep 18, 2025
-
Protein Rib Eye
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 100 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.