23 X 8
stanleys
Sep 10, 2025 · 5 min read
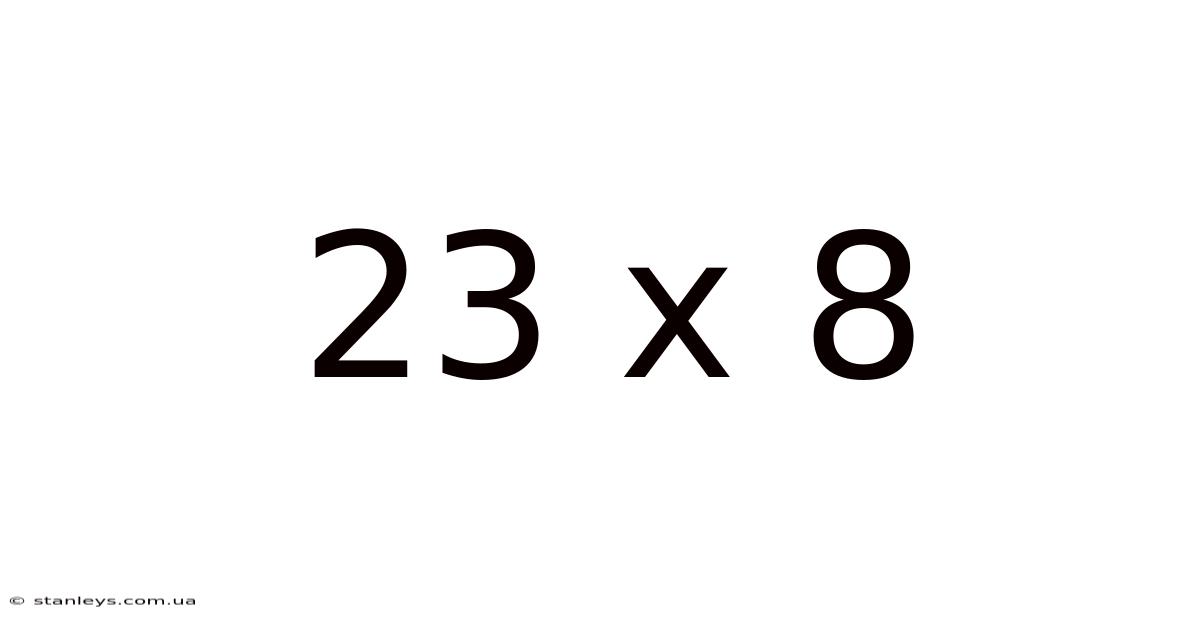
Table of Contents
Unveiling the Wonders of 23 x 8: A Deep Dive into Multiplication
This article explores the seemingly simple multiplication problem, 23 x 8, delving far beyond a mere numerical answer. We'll uncover the underlying mathematical principles, explore various methods for solving it, and even delve into its practical applications and surprising connections to other areas of mathematics. Understanding this single calculation can unlock a deeper appreciation for the elegance and power of mathematics. Let's embark on this journey of discovery!
Introduction: More Than Just a Number
At first glance, 23 multiplied by 8 appears straightforward. A quick calculation will yield the answer, but the true value lies in understanding the process and the broader mathematical concepts involved. This exploration will cater to diverse learners, from those just grasping multiplication fundamentals to those seeking a deeper mathematical understanding. We'll examine different calculation methods, discuss the properties of numbers involved, and touch upon related mathematical ideas.
Method 1: Traditional Multiplication
This is the method most commonly taught in schools. It involves breaking down the numbers and performing multiplication in stages:
- Multiply the units digit: 8 x 3 = 24. Write down '4' and carry-over '2'.
- Multiply the tens digit: 8 x 2 = 16. Add the carry-over '2': 16 + 2 = 18.
- Combine the results: The final answer is 184.
Therefore, 23 x 8 = 184. This method highlights the positional value of digits in our decimal system, a crucial concept in arithmetic.
Method 2: Distributive Property
The distributive property of multiplication over addition states that a(b + c) = ab + ac. We can use this to break down 23 into 20 + 3:
- Distribute the 8: 8 x (20 + 3) = (8 x 20) + (8 x 3)
- Multiply individually: (8 x 20) = 160 and (8 x 3) = 24
- Add the results: 160 + 24 = 184
This method provides a deeper understanding of the mathematical principles at play and is particularly useful for larger numbers. It emphasizes the relationship between addition and multiplication.
Method 3: Repeated Addition
This method, although less efficient for larger numbers, provides a strong visual representation of multiplication:
Simply add 23 eight times: 23 + 23 + 23 + 23 + 23 + 23 + 23 + 23 = 184. This method directly connects multiplication to repeated addition, strengthening the foundational understanding of the operation.
Method 4: Doubling and Halving
This method is a clever shortcut, particularly useful for mental calculation. Since 8 is 2³, we can double 23 three times:
- 23 x 2 = 46
- 46 x 2 = 92
- 92 x 2 = 184
This method demonstrates the power of recognizing patterns and utilizing mathematical properties to simplify calculations.
Exploring the Numbers: Prime Factorization
Let's analyze the numbers involved using prime factorization. Prime factorization is the process of expressing a number as a product of its prime factors (numbers divisible only by 1 and themselves).
- 23: This is a prime number itself.
- 8: This is 2 x 2 x 2 = 2³
The prime factorization of 184 (the product) can be found by combining the prime factors: 2³ x 23 = 184. This reveals the fundamental building blocks of the numbers and their relationship.
Applications and Real-World Connections
The seemingly simple calculation of 23 x 8 has numerous real-world applications:
- Counting objects: Imagine 23 rows of 8 chairs in an auditorium; the total number of chairs would be 184.
- Calculating costs: If an item costs $23 and you buy 8 of them, the total cost would be $184.
- Measurement and area: If a rectangle measures 23 units by 8 units, its area would be 184 square units.
- Data analysis: In various statistical contexts, multiplication is crucial for calculating totals, averages, and probabilities. This single calculation might represent a small part of a much larger dataset.
These examples demonstrate the practical relevance of this seemingly simple mathematical operation. It's a fundamental building block for numerous calculations in various fields.
Connections to Other Mathematical Concepts
This calculation touches upon several other mathematical concepts:
- Arithmetic: It is a core concept in arithmetic, emphasizing the fundamental operations of multiplication and addition.
- Algebra: It can be represented algebraically as 23 * 8 = x, where 'x' represents the unknown product.
- Number Theory: The prime factorization analysis connects to number theory, a branch of mathematics concerned with the properties of numbers.
- Geometry: Calculating areas of rectangles uses multiplication, directly linking this concept to geometric principles.
Frequently Asked Questions (FAQs)
-
Q: What is the easiest way to calculate 23 x 8? A: The method that feels most comfortable and intuitive will be the easiest. For many, the traditional multiplication method is straightforward. However, the distributive property or doubling method can also be quite efficient.
-
Q: Are there any tricks to quickly calculate this? A: Yes, the doubling method (explained above) is a quick mental math trick. Recognizing that 8 is 2³ allows for efficient doubling.
-
Q: Why is understanding the different methods important? A: Understanding different methods builds a more robust mathematical foundation. It improves problem-solving skills and provides flexibility in approaching similar problems. It also helps in understanding the underlying mathematical principles.
-
Q: Can this calculation be applied to more complex problems? A: Absolutely! The principles and methods used to solve 23 x 8 are fundamental to tackling much more complex multiplication problems and other mathematical challenges.
-
Q: What if I'm struggling with multiplication? A: Don't be discouraged! Practice consistently, starting with smaller numbers and gradually increasing the difficulty. Utilize different methods and seek help from teachers or educational resources when needed.
Conclusion: The Power of Understanding
While seemingly trivial, the multiplication problem 23 x 8 serves as a gateway to understanding a wealth of mathematical concepts and their practical applications. By exploring different solution methods and connecting it to other areas of mathematics, we've uncovered the deeper meaning and significance of this simple calculation. Remember, mathematical understanding is built not just on memorization, but on comprehension and the ability to connect seemingly disparate concepts. The journey of understanding 23 x 8 is a microcosm of the larger journey of mathematical exploration—a journey filled with elegance, discovery, and endless possibilities. The seemingly simple answer, 184, represents far more than just a numerical result; it represents the foundation of mathematical proficiency.
Latest Posts
Latest Posts
-
30 Of 210
Sep 11, 2025
-
40kilometers To Miles
Sep 11, 2025
-
75 Of 150
Sep 11, 2025
-
20 Of 65 00
Sep 11, 2025
-
76 1kg In Stone
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about 23 X 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.