75 Of 150
stanleys
Sep 11, 2025 · 5 min read
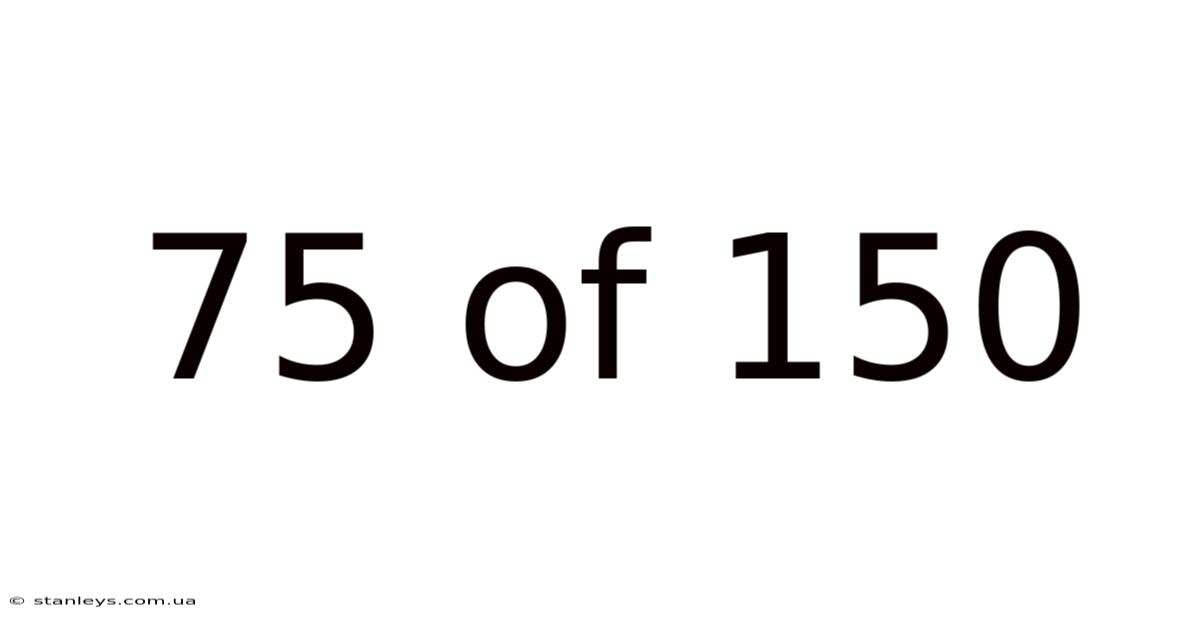
Table of Contents
Decoding the Fraction: Understanding 75 out of 150
What does it mean when someone says "75 out of 150"? This seemingly simple phrase represents a fundamental concept in mathematics: fractions, ratios, and percentages. Understanding how to interpret and manipulate these numerical relationships is crucial in various aspects of life, from academic assessments to everyday decision-making. This article will delve deep into the meaning of 75 out of 150, exploring its different representations, calculations, and real-world applications. We'll also address frequently asked questions to ensure a comprehensive understanding of this common mathematical concept.
Understanding the Basics: Fractions and Ratios
At its core, "75 out of 150" describes a fraction. A fraction represents a part of a whole. In this case, 75 represents the part, and 150 represents the whole. We can write this fraction as 75/150.
A closely related concept is a ratio. A ratio compares two quantities. The ratio of 75 to 150 can be written as 75:150, indicating that for every 75 units of one thing, there are 150 units of another. While fractions and ratios are distinct, they are often interchangeable, particularly when dealing with proportions.
Calculating the Percentage: From Fraction to Percentage
Converting a fraction to a percentage provides a more easily understood representation. Percentages express a fraction as a portion of 100. To convert 75/150 to a percentage, we follow these steps:
-
Divide the numerator by the denominator: 75 ÷ 150 = 0.5
-
Multiply the result by 100: 0.5 x 100 = 50%
Therefore, 75 out of 150 is equivalent to 50%. This means that 75 represents half (50%) of the total 150.
Simplifying Fractions: Finding the Lowest Common Denominator
The fraction 75/150 can be simplified by finding the greatest common divisor (GCD) of both the numerator and the denominator. The GCD of 75 and 150 is 75. Dividing both the numerator and denominator by 75, we get:
75 ÷ 75 = 1 150 ÷ 75 = 2
This simplifies the fraction to 1/2, which is still equivalent to 50%. Simplifying fractions makes them easier to understand and work with.
Real-World Applications: Where 75 out of 150 Matters
The concept of 75 out of 150, or 50%, has numerous real-world applications:
-
Academic Performance: If a student answers 75 questions correctly out of a total of 150, their score is 50%. This provides a clear indication of their understanding of the subject matter.
-
Sales and Marketing: If a company sets a sales target of 150 units and achieves 75, they've reached 50% of their goal. This data helps in assessing performance and making adjustments.
-
Surveys and Polls: If 75 out of 150 respondents agree with a particular statement, it represents a 50% agreement rate. This provides valuable insights into public opinion.
-
Manufacturing and Quality Control: If 75 out of 150 products pass quality inspection, the pass rate is 50%. This highlights areas for improvement in the manufacturing process.
-
Financial Analysis: A portfolio that achieves a 75% return on a 150% investment would be seen as a 50% return rate on investment. This is a key metric for evaluating investment performance.
Beyond the Basics: Exploring Proportions and Ratios Further
Understanding 75 out of 150 allows us to explore more complex proportional relationships. For instance:
-
Scaling Up: If a recipe calls for 75 grams of flour to make 150 cookies, how much flour is needed to make 300 cookies? Since 300 is double 150, we would double the flour amount: 75 grams x 2 = 150 grams.
-
Scaling Down: If a map has a scale where 75 cm represents 150 km in reality, how many kilometers does 37.5 cm represent? Since 37.5 is half of 75, the corresponding distance would be half of 150 km: 150 km ÷ 2 = 75 km.
These examples demonstrate the practical applications of understanding proportional relationships and the ability to scale quantities up or down based on a given ratio.
The Importance of Context: Why Understanding the Whole is Crucial
While the numerical calculation of 75 out of 150 is straightforward, the context is paramount. Understanding the meaning of the 150 (the total) is essential for proper interpretation. For instance:
-
75 correct answers out of 150 questions on a test indicates a 50% score. This might be considered passing or failing depending on the grading scale.
-
75 defective items out of 150 produced indicates a 50% defect rate, signifying a serious quality control problem.
-
75 sunny days out of 150 days in a season means 50% of the days were sunny. This represents a general description of the weather.
The same numerical result (50%) holds different levels of significance depending on the context.
Frequently Asked Questions (FAQ)
Q: How do I calculate the percentage of any fraction?
A: To calculate the percentage of any fraction, divide the numerator by the denominator and multiply the result by 100.
Q: What is the difference between a fraction and a ratio?
A: While similar, a fraction represents a part of a whole, whereas a ratio compares two quantities. They are often used interchangeably, especially when expressing proportions.
Q: Can 75/150 be simplified further?
A: Yes, 75/150 simplifies to 1/2.
Q: What if I have a different number of items, say 75 out of 200?
A: You would follow the same process: 75 ÷ 200 = 0.375, then multiply by 100 to get 37.5%.
Q: Is there a way to easily convert fractions to percentages mentally?
A: For simple fractions like 1/2, 1/4, and 3/4, mental conversion is straightforward. For more complex fractions, a calculator or mental arithmetic skills are helpful.
Conclusion: Mastering Fractions and Ratios
Understanding the meaning and implications of "75 out of 150" goes beyond simple arithmetic. It involves grasping the concepts of fractions, ratios, and percentages, and applying them to various real-world situations. The ability to interpret and manipulate these numerical relationships is a valuable skill applicable in diverse fields, from academic studies to business decisions. By mastering these fundamental mathematical concepts, you enhance your ability to analyze data, solve problems, and make informed decisions. The ability to convert fractions to percentages and simplify fractions provides efficiency and clarity in numerous applications. Remember that context is key; the same numerical results can have drastically different interpretations depending on the specific situation. Therefore, a thorough understanding of the underlying context is as vital as the numerical calculation itself.
Latest Posts
Latest Posts
-
47 7kg In Stone
Sep 11, 2025
-
3 Of 600
Sep 11, 2025
-
106km In Miles
Sep 11, 2025
-
20 Of 620
Sep 11, 2025
-
178 Pounds Kg
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about 75 Of 150 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.