30 Of 210
stanleys
Sep 11, 2025 · 6 min read
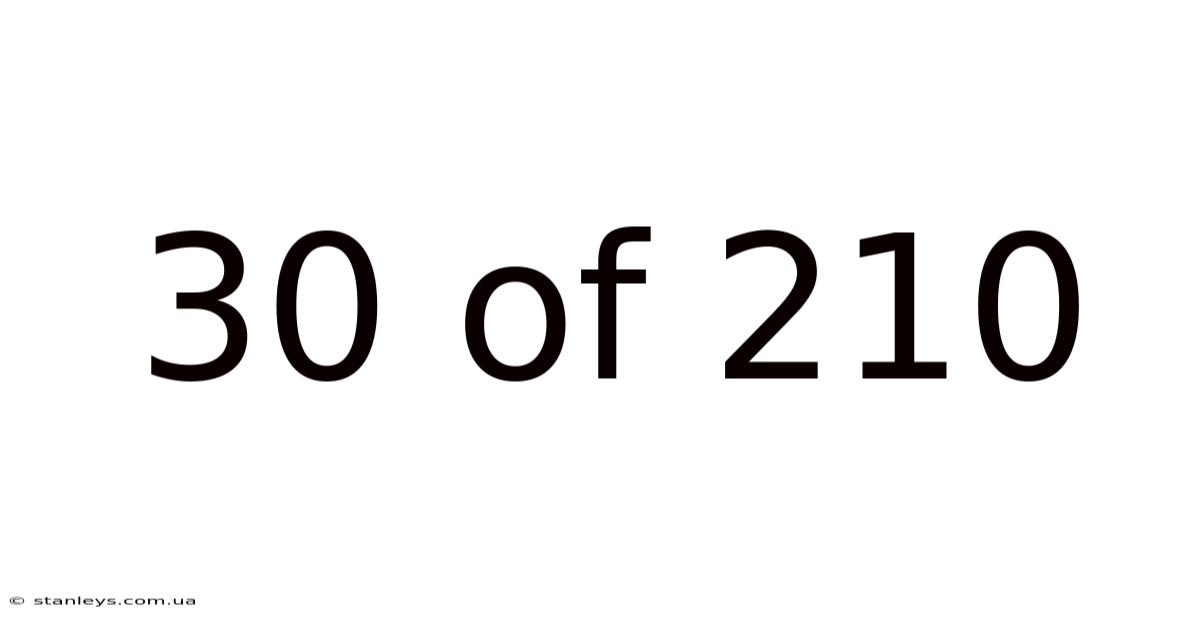
Table of Contents
Decoding the Enigma: A Deep Dive into 30/210 and its Implications
The seemingly simple fraction 30/210 might appear unremarkable at first glance. However, a closer examination reveals a wealth of mathematical concepts and practical applications, ranging from basic arithmetic to more advanced statistical analysis. This comprehensive exploration will delve into the various facets of 30/210, explaining its simplification, its representation in different mathematical contexts, and its potential uses in real-world scenarios. Understanding 30/210 provides a foundational stepping stone for grasping more complex mathematical ideas.
Introduction: Understanding Fractions
Before diving into the specifics of 30/210, let's refresh our understanding of fractions. A fraction represents a part of a whole. It is expressed as a ratio of two numbers, the numerator (the top number) and the denominator (the bottom number). The numerator indicates the number of parts we have, while the denominator indicates the total number of equal parts the whole is divided into. For instance, in the fraction 1/2, the numerator (1) signifies one part, and the denominator (2) signifies that the whole is divided into two equal parts.
Simplifying 30/210: Finding the Greatest Common Divisor (GCD)
The fraction 30/210 is not in its simplest form. To simplify a fraction, we need to find the Greatest Common Divisor (GCD) of the numerator and the denominator. The GCD is the largest number that divides both the numerator and denominator without leaving a remainder.
Several methods exist for finding the GCD. One common method is to list the factors of both numbers and identify the largest factor they share.
- Factors of 30: 1, 2, 3, 5, 6, 10, 15, 30
- Factors of 210: 1, 2, 3, 5, 6, 7, 10, 14, 15, 21, 30, 35, 42, 70, 105, 210
By comparing the lists, we see that the largest common factor is 30.
Alternatively, we can use the Euclidean algorithm, a more efficient method for larger numbers. The algorithm involves repeatedly dividing the larger number by the smaller number and replacing the larger number with the remainder until the remainder is 0. The last non-zero remainder is the GCD.
- Divide 210 by 30: 210 = 30 * 7 + 0 Since the remainder is 0, the GCD is 30.
Now, we divide both the numerator and the denominator of 30/210 by the GCD (30):
30 ÷ 30 = 1 210 ÷ 30 = 7
Therefore, the simplified form of 30/210 is 1/7.
Representing 30/210 in Different Contexts
The fraction 30/210, or its simplified form 1/7, can be represented in various ways:
- Decimal: 1/7 ≈ 0.142857... (This is a recurring decimal)
- Percentage: 1/7 ≈ 14.29%
- Ratio: 1:7
- Proportion: One out of seven.
These different representations highlight the versatility of fractions and their ability to express the same quantitative relationship in different formats, each suitable for different contexts and applications.
Real-World Applications of 30/210 (or 1/7)
The fraction 1/7, being the simplified form of 30/210, can be applied in numerous real-world situations:
- Probability: If you have a bag containing 7 equally likely marbles, and one is red, the probability of picking the red marble is 1/7.
- Ratio and Proportion: If a recipe calls for 7 parts of flour and 1 part of sugar, the ratio of sugar to flour is 1:7.
- Division: Sharing 30 items equally among 210 people would result in each person receiving 1/7 of an item.
- Data Analysis: If 30 out of 210 survey respondents answered “yes” to a question, the proportion of “yes” responses is 1/7.
These examples illustrate how understanding fractions like 30/210 translates to practical problem-solving in diverse fields.
Expanding on the Concept: Fractions and their Operations
Understanding 30/210 provides a springboard to explore various operations involving fractions:
-
Addition and Subtraction: To add or subtract fractions, they must have a common denominator. For example, adding 1/7 and 2/7 results in 3/7. If the denominators are different, find the least common multiple (LCM) and adjust the fractions accordingly.
-
Multiplication: Multiplying fractions is straightforward: multiply the numerators together and the denominators together. For example, (1/7) * (2/3) = 2/21.
-
Division: To divide fractions, invert the second fraction (reciprocal) and multiply. For example, (1/7) ÷ (2/3) = (1/7) * (3/2) = 3/14.
-
Comparing Fractions: Several methods exist to compare fractions. One is to find a common denominator and compare the numerators. Another is to convert the fractions to decimals and compare their decimal values.
Mastering these operations with simpler fractions like 1/7 forms a strong foundation for tackling more complex fractional calculations.
Further Exploration: Advanced Applications
Beyond basic arithmetic, the concept behind 30/210 and its simplified form 1/7 extends to more advanced mathematical fields:
-
Algebra: Fractions are integral to solving algebraic equations and inequalities. Understanding how to manipulate fractions is crucial for simplifying expressions and isolating variables.
-
Calculus: Derivatives and integrals frequently involve fractional expressions. A solid grasp of fraction manipulation is essential for success in calculus.
-
Statistics: Fractions and proportions are fundamental in statistical analysis, used in calculating probabilities, proportions, and relative frequencies.
-
Geometry: Fractions play a significant role in geometrical calculations, particularly when dealing with ratios, proportions, and areas of shapes.
Frequently Asked Questions (FAQ)
-
Q: Why is simplifying fractions important?
- A: Simplifying fractions makes them easier to understand, compare, and use in calculations. It presents the fraction in its most concise and efficient form.
-
Q: What if I can't find the GCD easily?
- A: Use the Euclidean algorithm; it's a systematic method to find the GCD of any two numbers.
-
Q: Are there other ways to represent 1/7?
- A: Yes, 1/7 can be represented as a decimal (approximately 0.142857), a percentage (approximately 14.29%), or a ratio (1:7).
-
Q: What are some common mistakes when working with fractions?
- A: Common mistakes include forgetting to find a common denominator before adding or subtracting, incorrectly multiplying or dividing fractions, and not simplifying the final answer.
Conclusion: The Significance of 30/210
The seemingly simple fraction 30/210, simplified to 1/7, serves as a powerful illustration of fundamental mathematical concepts. Understanding its simplification, its representation in different forms, and its real-world applications highlights the importance of grasping fractional arithmetic. This knowledge is not merely an academic pursuit; it’s a crucial skill applicable to diverse fields, from everyday problem-solving to advanced scientific and engineering calculations. Mastering the intricacies of fractions like 30/210 builds a robust foundation for more complex mathematical exploration and problem-solving in various aspects of life. The journey from 30/210 to 1/7 is a microcosm of the power of simplification and the importance of understanding the underlying mathematical principles.
Latest Posts
Latest Posts
-
47 7kg In Stone
Sep 11, 2025
-
3 Of 600
Sep 11, 2025
-
106km In Miles
Sep 11, 2025
-
20 Of 620
Sep 11, 2025
-
178 Pounds Kg
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about 30 Of 210 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.