23 X 12
stanleys
Sep 15, 2025 · 5 min read
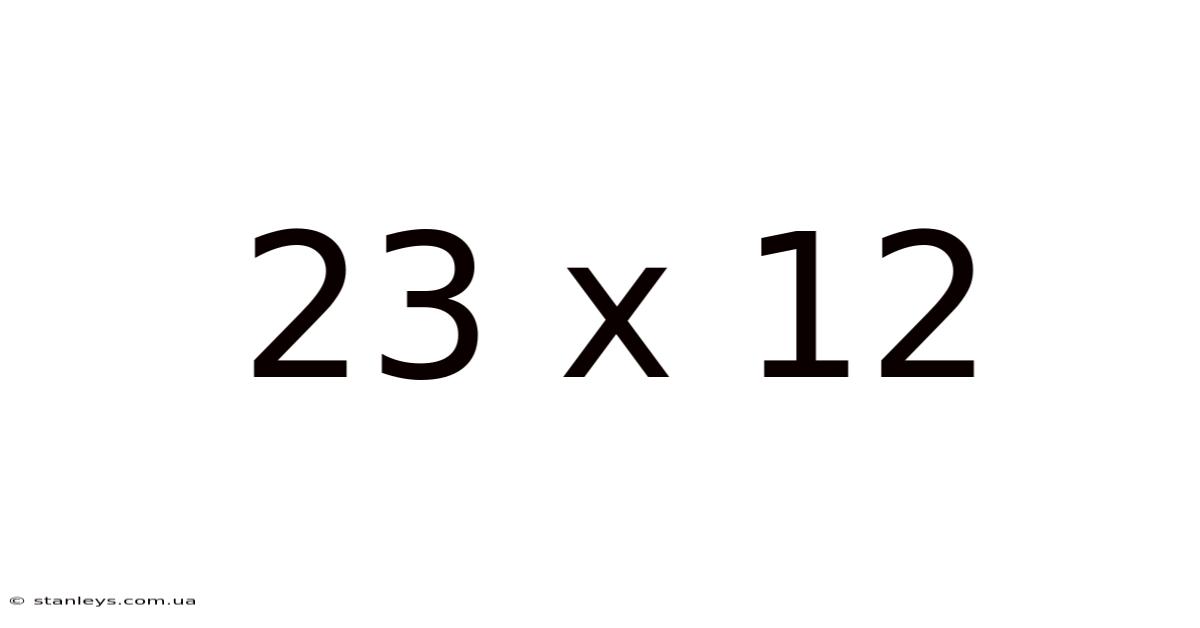
Table of Contents
Unveiling the Mysteries of 23 x 12: A Deep Dive into Multiplication
The seemingly simple equation of 23 x 12 might appear unremarkable at first glance. However, this seemingly basic multiplication problem provides a fantastic opportunity to explore various mathematical concepts, problem-solving strategies, and even delve into the historical context of multiplication itself. This article will unravel the mysteries of 23 x 12, providing multiple approaches to solving it, exploring the underlying principles, and addressing common misconceptions. Whether you're a student brushing up on your multiplication skills or a math enthusiast looking for a deeper understanding, this comprehensive guide will equip you with a wealth of knowledge.
Introduction: More Than Just a Number
The multiplication problem 23 x 12 is more than just a calculation; it's a gateway to understanding fundamental mathematical principles. It allows us to explore different methods of multiplication, from the traditional standard algorithm to more intuitive techniques like distributive property and mental math strategies. We’ll also touch upon the historical evolution of multiplication, showing how different cultures approached this vital arithmetic operation. Understanding this one problem can significantly improve your overall mathematical fluency and problem-solving abilities.
Method 1: The Standard Algorithm
The standard algorithm, taught in most schools, involves a systematic approach to multiplication. Let's break down 23 x 12 step-by-step:
-
Multiply 23 by 2 (the ones digit of 12):
- 2 x 3 = 6 (write 6)
- 2 x 2 = 4 (write 4 below the 6)
-
Multiply 23 by 10 (the tens digit of 12): Notice we add a zero as a placeholder in the ones column because we're multiplying by 10.
- 1 x 3 = 3 (write 3 under the 4)
- 1 x 2 = 2 (write 2 under the 3)
-
Add the partial products:
23 x12 ---- 46 230 ---- 276
Therefore, 23 x 12 = 276.
Method 2: The Distributive Property
The distributive property states that a(b + c) = ab + ac. We can apply this to our problem by breaking down 12 into 10 and 2:
-
Break down the problem: 23 x (10 + 2)
-
Apply the distributive property: (23 x 10) + (23 x 2)
-
Calculate the individual products: 230 + 46
-
Add the results: 230 + 46 = 276
This method demonstrates a deeper understanding of the underlying mathematical principles and can be particularly useful for mental calculations.
Method 3: Lattice Multiplication
Lattice multiplication, a visually appealing method, offers a structured approach:
-
Draw a lattice: Create a grid with two rows (for the digits of 23) and two columns (for the digits of 12).
-
Multiply and fill the squares: Multiply each digit from 23 with each digit from 12 and write the result in the corresponding cell, separating the tens and ones digits diagonally.
-
Sum the diagonals: Add the numbers along each diagonal, carrying over to the next diagonal if necessary.
2 | 3 ------ 1 | 2 | 6 | 6 1 | 4 | 3 | 0 ------ 2 | 7 | 6
The result, reading from the top left to bottom right, is 276.
Method 4: Mental Math Techniques
For those proficient in mental arithmetic, several strategies can be employed to solve 23 x 12 mentally:
-
Breaking down the numbers: This involves breaking down 23 into 20 + 3 and 12 into 10 + 2. Then, calculate (20 x 10) + (20 x 2) + (3 x 10) + (3 x 2) = 200 + 40 + 30 + 6 = 276.
-
Using doubling and halving: Double 23 to get 46, and halve 12 to get 6. Then, multiply 46 x 6 = 276.
-
Rounding and adjusting: Round 23 to 20 and 12 to 10. Calculate 20 x 10 = 200. Then, account for the difference: (3 x 12) + (2 x 20) = 36 + 40 = 76. Finally, add 200 + 76 = 276.
The effectiveness of mental math techniques depends heavily on individual mathematical skills and practice.
The Historical Context of Multiplication
Multiplication, as a concept, has evolved over millennia. Ancient civilizations used various methods for multiplication, often employing techniques based on addition, subtraction, and doubling. The Egyptians, for instance, used a system of doubling and halving, while the Babylonians developed sophisticated multiplication tables. The development of the Hindu-Arabic numeral system and the positional notation we use today significantly simplified multiplication.
The evolution of calculating tools, from the abacus to slide rules and eventually electronic calculators and computers, has further accelerated the ease and speed of performing multiplication calculations.
Addressing Common Errors and Misconceptions
Several common errors can arise when performing multiplication, particularly with larger numbers like 23 x 12. These include:
- Incorrect placement of partial products: Failing to align the digits correctly when adding the partial products can lead to incorrect results.
- Errors in carrying over: Forgetting to carry over tens or hundreds when performing addition within the multiplication process is a frequent mistake.
- Misunderstanding the distributive property: Incorrectly applying the distributive property can result in inaccurate calculations.
Careful attention to detail and a thorough understanding of the underlying principles are crucial for avoiding these errors.
Further Exploration: Beyond 23 x 12
The principles learned through solving 23 x 12 are applicable to a wide range of mathematical problems. Understanding multiplication is fundamental for more advanced mathematical concepts, including:
- Algebra: Multiplication is crucial for manipulating algebraic expressions and solving equations.
- Geometry: Calculating areas and volumes often involves multiplication.
- Calculus: Differentiation and integration utilize the principles of multiplication.
Conclusion: Mastering Multiplication, One Problem at a Time
Solving 23 x 12 is not just about arriving at the answer (276). It’s about grasping the multiple approaches to solving it, understanding the underlying mathematical principles, and appreciating the historical context of multiplication. By exploring different methods and understanding common pitfalls, you enhance your mathematical skills and develop a deeper appreciation for the elegance and power of mathematics. This seemingly simple problem serves as a microcosm of the broader world of mathematics, highlighting the beauty of diverse problem-solving strategies and the enduring importance of fundamental mathematical concepts. Remember that consistent practice and a curious mindset are key to mastering multiplication and advancing your mathematical journey.
Latest Posts
Latest Posts
-
52 4kg In Stone
Sep 15, 2025
-
30 Of 27
Sep 15, 2025
-
35 12
Sep 15, 2025
-
25oz To Grams
Sep 15, 2025
-
25 Of 230
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 23 X 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.