25 Of 230
stanleys
Sep 15, 2025 · 6 min read
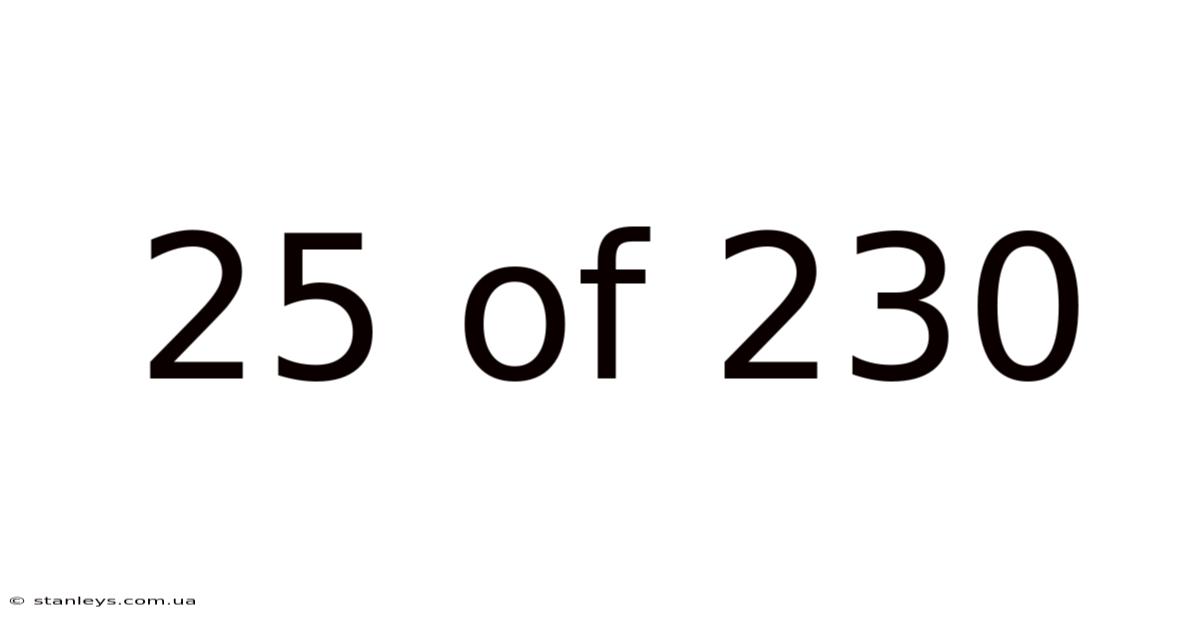
Table of Contents
Decoding the Mystery: Understanding the Fraction 25/230 and its Implications
The fraction 25/230 might seem insignificant at first glance, a small number lost in the vast ocean of mathematical possibilities. However, understanding this seemingly simple fraction opens doors to a deeper appreciation of fractions, ratios, percentages, and their applications in various fields. This article will explore 25/230 in detail, examining its simplification, decimal equivalent, percentage representation, and practical applications, providing a comprehensive understanding for students and enthusiasts alike. We'll also delve into the broader mathematical concepts surrounding fractions and their importance in everyday life.
I. Simplifying the Fraction 25/230
The first step in understanding any fraction is to simplify it to its lowest terms. This involves finding the greatest common divisor (GCD) of the numerator (25) and the denominator (230) and dividing both by that number.
The factors of 25 are 1, 5, and 25. The factors of 230 are 1, 2, 5, 10, 23, 46, 115, and 230.
The greatest common divisor of 25 and 230 is 5. Therefore, we can simplify the fraction as follows:
25 ÷ 5 = 5 230 ÷ 5 = 46
Thus, 25/230 simplifies to 5/46. This simplified fraction is equivalent to the original fraction but is easier to work with in calculations.
II. Converting to Decimal
Converting a fraction to a decimal is a fundamental skill in mathematics. To convert 5/46 to a decimal, we simply divide the numerator (5) by the denominator (46):
5 ÷ 46 ≈ 0.10869565
This decimal is an approximation because the division results in a non-terminating decimal. Rounding to a specific number of decimal places depends on the required level of accuracy. For many practical purposes, rounding to three decimal places (0.109) would be sufficient.
III. Expressing as a Percentage
Percentages are a common way to express fractions and decimals, particularly in contexts involving proportions and comparisons. To convert the simplified fraction 5/46 to a percentage, we first convert it to a decimal (as shown above) and then multiply by 100:
0.10869565 × 100 ≈ 10.87%
Again, rounding is necessary. In this case, we've rounded to two decimal places, giving us approximately 10.87%. This indicates that 5/46 represents approximately 10.87% of a whole.
IV. Real-World Applications of Fractions like 25/230
Fractions are ubiquitous in daily life, appearing in various contexts, from cooking and shopping to finance and engineering. Understanding fractions is crucial for problem-solving in these areas. Let's consider some examples related to the fraction 25/230 (or its simplified form, 5/46):
-
Proportion and Ratio: Imagine a classroom with 230 students. If 25 students are absent, the fraction 25/230 represents the proportion of absent students. The simplified fraction, 5/46, makes it easier to see that approximately one-tenth of the students are absent.
-
Probability: If you have a bag containing 230 marbles, with 25 of them being red, the probability of picking a red marble at random is 25/230, or 5/46. This simplified fraction helps to visualize the chance of this event occurring.
-
Measurement and Scaling: In construction or engineering, fractions are used for precise measurements. For example, 25/230 of a meter could represent a specific length in a design.
-
Finance and Budgeting: Fractions can be used to represent parts of a budget or investment. For instance, 25/230 of a total budget could be allocated to a specific project.
-
Data Analysis: In statistical analysis, fractions are essential for representing proportions and calculating various metrics. The ability to easily manipulate and understand fractions is critical for data interpretation.
V. Expanding on Fraction Concepts: Numerator, Denominator, and Equivalent Fractions
Before moving further, let's solidify our understanding of fundamental fraction concepts. A fraction consists of two parts: the numerator (the top number) and the denominator (the bottom number). The numerator represents the number of parts we have, while the denominator represents the total number of equal parts the whole is divided into.
Equivalent fractions represent the same value even though they have different numerators and denominators. For example, 25/230, 5/46, 10/92, and so on are all equivalent fractions. They all represent the same proportion of a whole.
VI. Advanced Concepts: Rational Numbers and Operations with Fractions
Fractions are a subset of rational numbers, which are numbers that can be expressed as the ratio of two integers (where the denominator is not zero). Understanding rational numbers is crucial for comprehending more complex mathematical operations.
Operations with fractions, including addition, subtraction, multiplication, and division, are essential mathematical skills. These operations are fundamental for solving various real-world problems. For instance, adding fractions might be necessary when combining portions of ingredients in a recipe, while multiplying fractions is used in calculating discounts or area.
VII. The Importance of Understanding Fractions
Proficiency in working with fractions is crucial for success in many aspects of life. It's not merely a mathematical concept; it's a practical skill with far-reaching applications. The ability to understand and manipulate fractions helps in:
-
Problem Solving: Fractions are essential tools for solving a wide range of problems in diverse fields.
-
Critical Thinking: Working with fractions enhances analytical and critical thinking skills.
-
Decision Making: Understanding proportions and ratios aids in making informed decisions in various situations.
-
Financial Literacy: Fractions are crucial for managing finances effectively.
-
Everyday Life: From cooking and baking to understanding sales and discounts, fractions are integral to daily activities.
VIII. Frequently Asked Questions (FAQ)
Q1: Why is it important to simplify fractions?
A1: Simplifying fractions makes them easier to work with in calculations, comparisons, and visualizations. It provides a clearer representation of the underlying proportion.
Q2: How do I find the greatest common divisor (GCD)?
A2: Several methods exist for finding the GCD, including listing factors, using prime factorization, and employing the Euclidean algorithm. The method chosen depends on the complexity of the numbers involved.
Q3: Can a fraction have a denominator of zero?
A3: No, a fraction cannot have a denominator of zero. Division by zero is undefined in mathematics.
Q4: What are some common errors to avoid when working with fractions?
A4: Common errors include incorrect simplification, improper addition/subtraction without finding a common denominator, and mistakes in multiplying/dividing fractions. Careful attention to detail and understanding of the rules are crucial.
Q5: How can I improve my understanding of fractions?
A5: Practice is key. Work through various examples, solve problems, and use visual aids to reinforce your understanding. There are many online resources and educational materials available to help.
IX. Conclusion
The seemingly simple fraction 25/230, when explored in depth, reveals a rich tapestry of mathematical concepts and practical applications. From simplifying fractions to converting them to decimals and percentages, and understanding their use in diverse real-world scenarios, this article aims to provide a comprehensive overview. The ability to manipulate and understand fractions is a fundamental skill that extends far beyond the classroom, impacting various aspects of our lives. Mastering fractions empowers us to solve problems, make informed decisions, and navigate the world with increased confidence and precision. Continuous practice and exploration of related concepts will solidify this vital mathematical understanding.
Latest Posts
Latest Posts
-
19 20 To Decimal
Sep 15, 2025
-
Author Sarah Knight
Sep 15, 2025
-
4 Of 80
Sep 15, 2025
-
Pg To Ng
Sep 15, 2025
-
99f In C
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 25 Of 230 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.