35 - 12
stanleys
Sep 15, 2025 · 6 min read
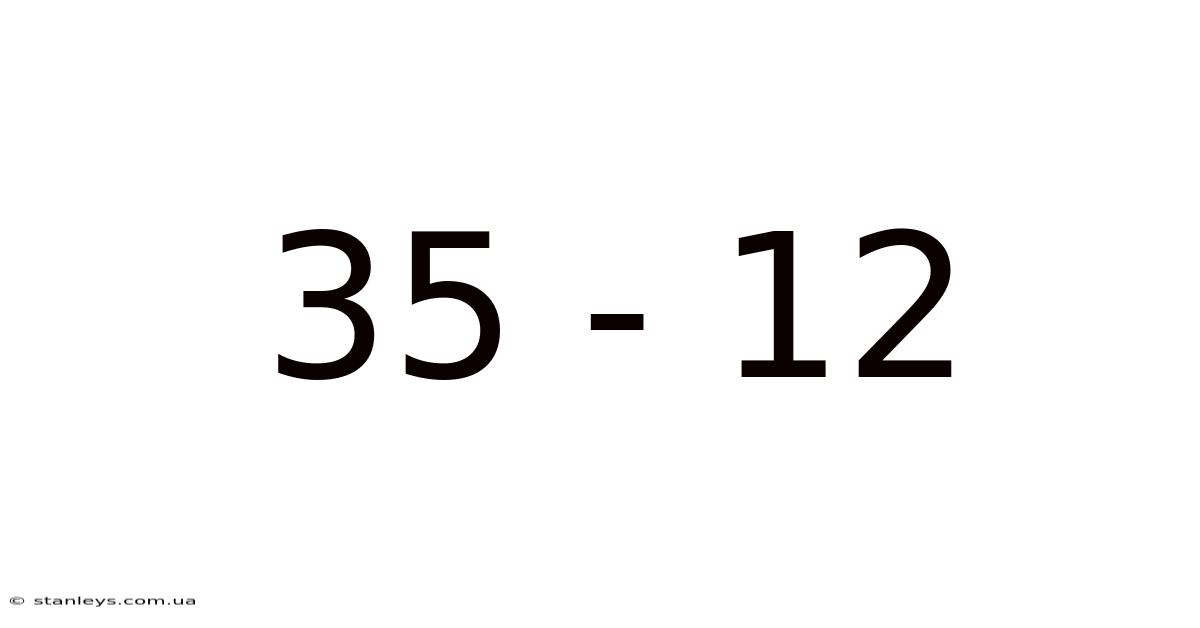
Table of Contents
Understanding Subtraction: A Deep Dive into 35 - 12
This article explores the seemingly simple subtraction problem, 35 - 12, delving beyond the basic answer to understand the underlying mathematical concepts and different methods for solving it. We'll cover various approaches, from the standard algorithm to more intuitive methods, making this explanation accessible for learners of all ages and backgrounds. Understanding subtraction is fundamental to mathematical literacy, and this comprehensive guide will equip you with a solid grasp of this essential operation.
Introduction: The Basics of Subtraction
Subtraction is one of the four basic arithmetic operations, alongside addition, multiplication, and division. It represents the process of removing a quantity from another quantity. In the problem 35 - 12, we are removing 12 units from a total of 35 units. The result, or difference, tells us how many units are left. While seemingly straightforward for many, understanding the mechanics behind subtraction is key to tackling more complex problems later on. This article aims to solidify that understanding.
Method 1: The Standard Algorithm (Borrowing/Regrouping)
This is the most commonly taught method in schools. It involves working with the numbers digit by digit, starting from the rightmost column (the ones column).
Steps:
-
Ones Column: We start by subtracting the ones digits: 5 - 2 = 3.
-
Tens Column: Now, we move to the tens column. We need to subtract 1 (from 12) from 3 (from 35). This is a simple subtraction: 3 - 1 = 2.
-
Result: Combining the results from the ones and tens columns, we get 23. Therefore, 35 - 12 = 23.
This method, while effective, relies on the concept of regrouping or borrowing, which can sometimes be challenging for beginners to grasp. Let's examine this concept more closely.
Understanding Regrouping:
Imagine you have 3 tens and 5 ones (representing 35). To subtract 12 (1 ten and 2 ones), we first try to subtract 2 ones from 5 ones. This works easily. But when we move to the tens column, we face a problem: we can't directly subtract 1 ten from 3 tens because that would leave us with a negative value in the tens column. To overcome this, we "borrow" one ten from the tens column and convert it into 10 ones. Now we have 2 tens and 15 ones (still representing 35). Subtracting 2 ones leaves 13 ones, and subtracting 1 ten leaves 2 tens, giving us the answer 23.
Method 2: Number Line Subtraction
A visual approach can enhance understanding, especially for visual learners. Using a number line, we can represent the subtraction as a movement backwards along the number line.
Steps:
-
Start at 35: Locate 35 on the number line.
-
Move 12 units to the left: This represents subtracting 12. Moving 10 units left takes us to 25. Moving another 2 units left brings us to 23.
-
Result: The final position on the number line (23) is the answer to the subtraction.
This method visually demonstrates the concept of reducing a quantity by showing the movement along the number line. It's a great way to introduce subtraction conceptually before diving into the standard algorithm.
Method 3: Decomposition Method
This method involves breaking down the numbers into smaller, easier-to-manage parts.
Steps:
-
Decompose 35: We can decompose 35 as 30 + 5.
-
Decompose 12: We can decompose 12 as 10 + 2.
-
Subtract the tens: 30 - 10 = 20.
-
Subtract the ones: 5 - 2 = 3.
-
Combine the results: 20 + 3 = 23. Thus, 35 - 12 = 23.
This approach emphasizes the place value of digits and simplifies the subtraction process by breaking it down into smaller, less daunting steps. This is especially useful for younger learners still developing their understanding of place value.
Method 4: Using Addition (Inverse Operation)
Subtraction and addition are inverse operations; one undoes the other. We can use this relationship to solve subtraction problems.
Steps:
-
Think: What number added to 12 equals 35? This is essentially asking the inverse of the subtraction problem.
-
Solve using addition: We can mentally or using written addition, find the number that, when added to 12, results in 35.
-
Result: The answer is 23 (12 + 23 = 35).
This method requires a strong understanding of addition facts and can be a powerful mental math technique.
The Importance of Place Value in Subtraction
The concept of place value is crucial for understanding and accurately performing subtraction, especially with larger numbers. The value of a digit depends on its position within the number. In 35, the 3 represents 3 tens (30), and the 5 represents 5 ones (5). Understanding this allows for the accurate application of regrouping and decomposition methods.
Subtraction in Different Contexts: Real-World Applications
Subtraction is not just an abstract mathematical concept; it's used extensively in everyday life:
- Shopping: Calculating change after a purchase involves subtraction.
- Cooking: Adjusting recipes often requires subtracting ingredients.
- Finance: Tracking expenses and managing budgets heavily relies on subtraction.
- Measurement: Determining differences in length, weight, or volume necessitates subtraction.
- Time: Calculating elapsed time involves subtraction.
Frequently Asked Questions (FAQ)
Q: What if I try to subtract a larger number from a smaller number?
A: This results in a negative number. For example, 12 - 35 = -23. Negative numbers represent values less than zero.
Q: Are there other methods to subtract besides the ones mentioned?
A: Yes, there are various other methods and techniques, including using visual aids like counters or blocks, using mental math strategies, and applying different algorithms depending on the complexity of the numbers involved.
Q: Why is it important to learn different methods for subtraction?
A: Learning multiple methods allows for flexibility and choosing the most efficient approach based on the specific problem and individual preference. It also fosters a deeper understanding of the underlying mathematical principles.
Conclusion: Mastering Subtraction – A Building Block for Mathematical Success
Mastering subtraction is a fundamental stepping stone in mathematical learning. It's not merely about obtaining the correct answer (23 in this case) but understanding why that answer is correct and the various paths to achieving it. Through different methods—the standard algorithm, number lines, decomposition, and using addition—we've explored multiple ways to approach 35 - 12, highlighting the importance of place value and the interconnectedness of mathematical operations. By grasping these concepts, learners build a solid foundation for more advanced mathematical concepts and problem-solving skills. The seemingly simple subtraction problem 35 - 12, therefore, serves as a gateway to a deeper appreciation of the elegance and power of mathematics. Remember, consistent practice and a conceptual understanding are key to mastering this crucial skill.
Latest Posts
Latest Posts
-
2 X 6x
Sep 15, 2025
-
70 Of 180
Sep 15, 2025
-
19 20 To Decimal
Sep 15, 2025
-
Author Sarah Knight
Sep 15, 2025
-
4 Of 80
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 35 - 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.