200 / 15
stanleys
Sep 13, 2025 · 6 min read
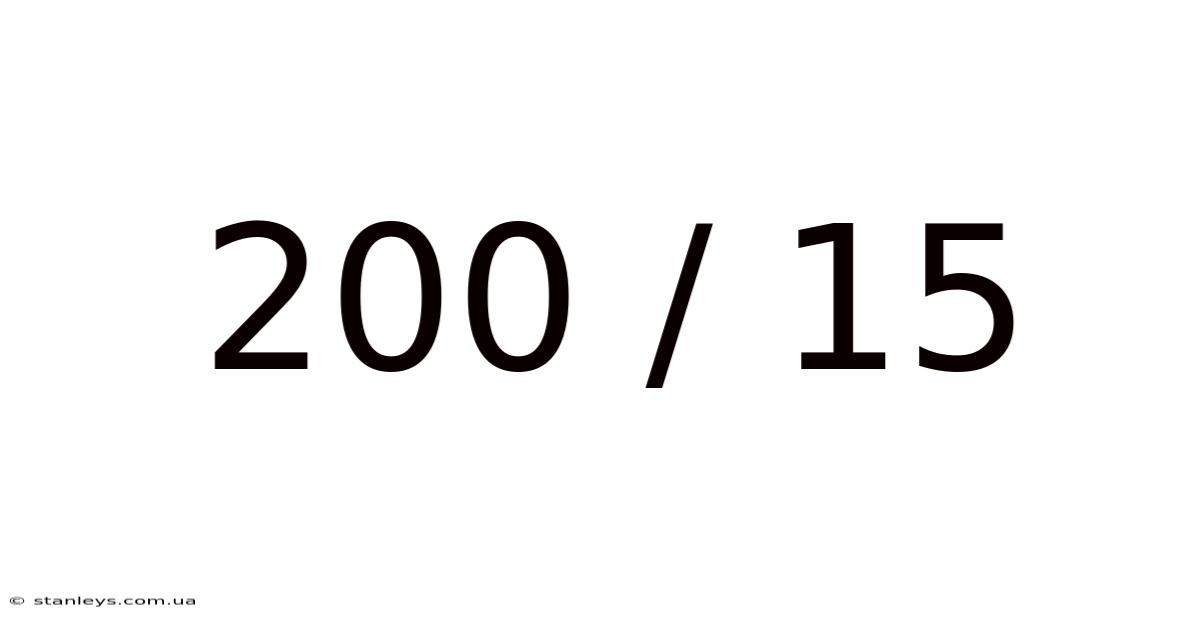
Table of Contents
Decoding 200/15: Understanding Ratios, Fractions, and Their Applications
This article delves into the seemingly simple ratio 200/15, exploring its mathematical foundations, various interpretations, simplification techniques, and practical applications across diverse fields. We'll go beyond a simple calculation, uncovering the underlying principles and showcasing the versatility of this ratio in real-world scenarios. Understanding ratios like 200/15 is fundamental to various disciplines, from cooking and construction to finance and data analysis. This guide aims to demystify this seemingly basic concept and build a solid understanding of its implications.
Understanding Ratios and Fractions
At its core, 200/15 represents a ratio. A ratio is a comparison of two or more quantities. It shows the relative sizes of the quantities. In this case, we're comparing 200 to 15. This ratio can also be expressed as a fraction, where 200 is the numerator (the top number) and 15 is the denominator (the bottom number). Understanding this interchangeability is crucial. Fractions and ratios provide a concise way to represent relationships between quantities.
Simplifying the Ratio 200/15
Before exploring applications, let's simplify the ratio. Simplification involves finding the greatest common divisor (GCD) of the numerator and the denominator and dividing both by it. The GCD of 200 and 15 is 5.
- Dividing both the numerator and the denominator by 5, we get: 200/5 = 40 and 15/5 = 3.
Therefore, the simplified ratio is 40/3. This simplified form is equivalent to the original ratio, but it's easier to work with and understand. This process of simplification is essential for clearer interpretation and easier calculations.
Different Interpretations of 40/3
The simplified ratio 40/3 can be interpreted in several ways:
-
As an improper fraction: 40/3 means 40 divided by 3. This results in a mixed number.
-
As a mixed number: Performing the division, we find that 40 divided by 3 is 13 with a remainder of 1. This can be expressed as 13 1/3. This representation is often more intuitive in practical applications.
-
As a decimal: Converting the fraction 40/3 to a decimal yields approximately 13.333... This recurring decimal represents the precise value of the ratio.
Practical Applications of the Ratio 40/3
The ratio 40/3, derived from 200/15, has a wide range of practical applications:
1. Cooking and Baking:
Imagine a recipe that calls for 200 grams of flour and 15 grams of baking powder. The ratio of flour to baking powder is 200/15, or 40/3. If you want to scale the recipe down, you can use this simplified ratio. For example, to make a smaller batch, you might use 40 grams of flour and 3 grams of baking powder, maintaining the same proportion.
2. Construction and Engineering:
In construction, ratios are used extensively. For instance, the ratio of cement to sand in a concrete mix might be expressed as a ratio. A ratio like 40/3 might represent the relative proportions of two different materials needed for a specific structural element. Understanding these ratios ensures the structural integrity and durability of the construction.
3. Finance and Investment:
Ratios are fundamental in financial analysis. For example, the price-to-earnings ratio (P/E ratio) is a common metric used to evaluate the relative value of a company's stock. While not directly related to 40/3, this exemplifies the widespread use of ratios in assessing financial health and investment potential. Understanding ratios allows for informed financial decisions.
4. Data Analysis and Statistics:
Ratios are used extensively in statistics to compare different data sets or to represent proportions within a data set. For instance, the ratio of men to women in a particular population could be expressed as a ratio. Analyzing ratios helps reveal trends and patterns within the data. In data analysis, understanding ratios contributes to drawing meaningful conclusions.
Mathematical Operations with Ratios
Working with ratios involves several mathematical operations:
-
Addition and Subtraction: Adding or subtracting ratios requires a common denominator. For example, adding 40/3 and another ratio would require converting both ratios to have the same denominator.
-
Multiplication: Multiplying ratios involves multiplying the numerators and multiplying the denominators separately.
-
Division: Dividing ratios involves inverting the second ratio and then multiplying. This is crucial for understanding proportional relationships.
Proportions and Ratios
A proportion is a statement that two ratios are equal. For example, 200/15 = 40/3 is a proportion. Proportions are useful for solving problems involving scaling, such as adjusting recipes or determining unknown quantities in a proportional relationship. Understanding proportions allows us to solve real-world problems involving ratios.
Advanced Applications: Scale and Proportionality
The concept extends beyond simple calculations. Understanding the ratio 40/3 allows us to scale quantities proportionally. If we know one part of a proportion, we can use the ratio to find the other. For instance, if we know we need 120 grams of one ingredient (related to the 40 in the 40/3 ratio), we can use proportionality to determine the required amount of the other ingredient (related to the 3).
Further Exploration: Percentage Representation
The ratio 40/3 can also be expressed as a percentage. To do this, we divide the numerator by the denominator and multiply by 100:
(40/3) * 100 ≈ 1333.33%
This percentage representation shows that the first quantity is approximately 1333.33% of the second quantity. This alternate representation provides another perspective on the ratio's meaning.
Frequently Asked Questions (FAQ)
Q: What is the simplest form of the ratio 200/15?
A: The simplest form of 200/15 is 40/3.
Q: How do I convert 40/3 to a decimal?
A: To convert 40/3 to a decimal, divide 40 by 3. This yields approximately 13.333...
Q: What are some real-world examples of using ratios?
A: Ratios are used in cooking, construction, finance, data analysis, and many other fields.
Q: How do I solve problems using proportions?
A: Solving problems using proportions involves setting up an equation with two equal ratios and solving for the unknown variable.
Conclusion
The ratio 200/15, simplified to 40/3, is more than just a simple fraction. It represents a fundamental mathematical concept with wide-ranging practical applications. Understanding how to simplify ratios, interpret them in different forms (fraction, mixed number, decimal, percentage), and apply them to real-world problems is crucial for success in various fields. This article has provided a comprehensive overview, equipping you with the knowledge and tools to confidently tackle ratios in any context. Remember, the seemingly simple ratio holds a significant power in understanding and representing the relationships between quantities. Mastering the concepts discussed here will empower you to tackle more complex mathematical and real-world challenges with greater confidence.
Latest Posts
Latest Posts
-
80 Of 150
Sep 13, 2025
-
Rpm In Rad Sec
Sep 13, 2025
-
450ml In Ounces
Sep 13, 2025
-
Factor For 42
Sep 13, 2025
-
Antonyms For Respite
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 200 / 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.