15 Divided 2
stanleys
Sep 17, 2025 · 6 min read
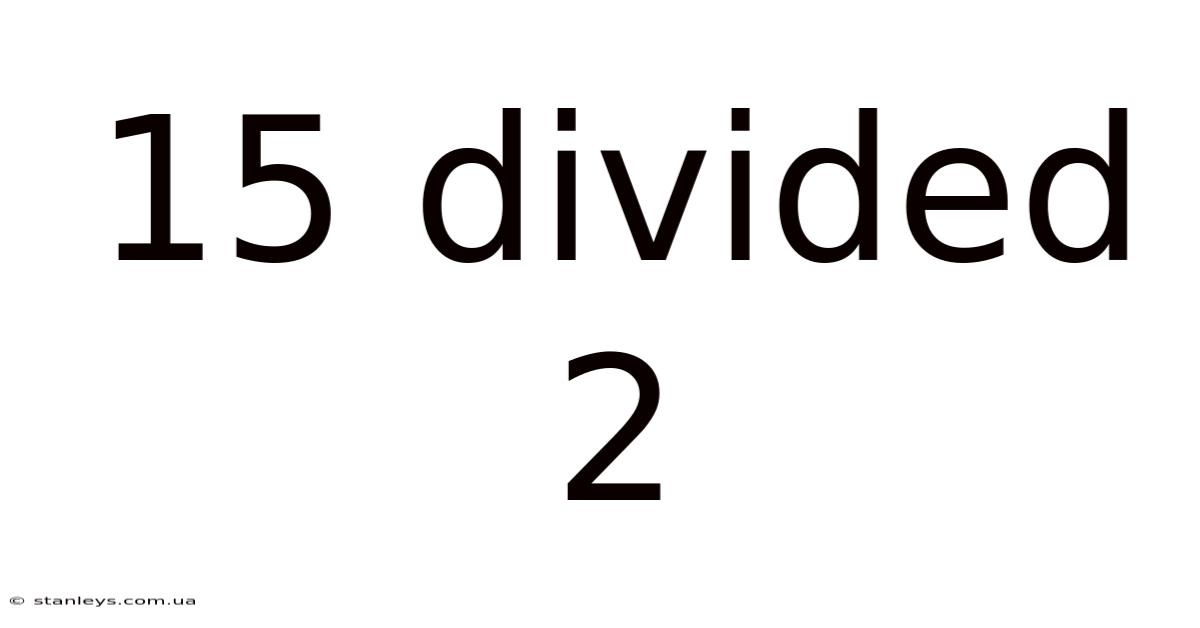
Table of Contents
15 Divided by 2: A Deep Dive into Division and its Applications
Understanding division is fundamental to mathematics, forming the bedrock for more complex calculations and problem-solving. This article explores the seemingly simple problem of 15 divided by 2, delving deep into the process, its various interpretations, and its significance across numerous fields. We'll move beyond the basic answer and uncover the nuances that make this concept so crucial in our understanding of the world around us.
Introduction: Beyond the Obvious Answer
At its most basic level, 15 divided by 2 (15 ÷ 2) equals 7.5 or 7 ½. This is easily obtained using a calculator or through long division. However, this simple answer hides a wealth of mathematical richness and practical applications. This article will unpack this seemingly straightforward calculation, examining its different interpretations, exploring the underlying concepts, and highlighting its relevance in various real-world scenarios. We will cover different methods of calculating the division, discuss the concepts of quotients, remainders, and decimals, and illustrate the applications of this basic division in areas like geometry, statistics, and everyday life.
Methods for Calculating 15 Divided by 2
Several methods can be used to calculate 15 divided by 2, each offering a different perspective on the problem:
-
Long Division: This classic method involves systematically dividing the dividend (15) by the divisor (2). We begin by seeing how many times 2 goes into 1 (zero), then move to 15. 2 goes into 15 seven times (2 x 7 = 14), leaving a remainder of 1. This remainder can be expressed as a fraction (1/2) or a decimal (0.5), resulting in the answer 7.5 or 7 ½.
-
Fraction Representation: Expressing the division as a fraction (15/2) immediately highlights the concept of a ratio. This fraction can then be simplified or converted to a decimal by dividing the numerator (15) by the denominator (2), yielding 7.5.
-
Repeated Subtraction: This method involves repeatedly subtracting the divisor (2) from the dividend (15) until the remainder is less than the divisor. Subtracting 2 seven times from 15 leaves a remainder of 1. This method reinforces the idea of division as repeated subtraction.
-
Calculator: The simplest approach is to use a calculator, which directly provides the answer 7.5. While convenient, understanding the underlying mathematical principles is crucial for problem-solving beyond simple calculations.
Understanding Quotients and Remainders
When we divide 15 by 2 using long division, we obtain a quotient of 7 and a remainder of 1. The quotient represents the number of times the divisor (2) goes completely into the dividend (15), while the remainder is the amount left over after the complete divisions. The remainder is crucial, as it indicates that the division is not exact; 15 cannot be perfectly divided into equal groups of 2.
The remainder can be expressed in different ways:
-
As a fraction: The remainder (1) becomes the numerator, and the divisor (2) becomes the denominator, resulting in the fraction 1/2. This gives us the mixed number 7 1/2.
-
As a decimal: The remainder can be converted into a decimal by dividing the remainder by the divisor (1 ÷ 2 = 0.5). This yields the decimal representation 7.5.
Applications of 15 Divided by 2 in Real-World Scenarios
The simple division of 15 by 2 has far-reaching applications across numerous fields:
-
Sharing Resources: If you have 15 cookies to share equally among 2 friends, each friend gets 7 cookies, and you have 1 cookie left over.
-
Geometry: Calculating the area or perimeter of shapes might involve division. For example, finding the average side length of a polygon with a total perimeter of 15 units and 2 sides.
-
Statistics: Averaging data often involves division. If you have two measurements totaling 15 units, the average is 7.5 units.
-
Finance: Dividing expenses or profits equally between partners or shareholders uses the principles of division.
-
Cooking & Baking: Scaling recipes up or down involves adjusting ingredient amounts proportionally, often requiring division. If a recipe calls for 15 grams of flour and you need to halve the recipe, you'd need 7.5 grams of flour.
-
Construction & Engineering: Calculating material quantities, dividing workloads among teams, and even determining the precise measurements for building projects all require using division.
-
Everyday Life: The principles of division are fundamental in almost every aspect of our day to day lives. From splitting bills equally amongst friends to determining how many bus rides it takes to reach your destination when the total distance is 15 km and each trip is 2km.
Decimal Representation and its Significance
The decimal representation, 7.5, introduces the concept of decimal numbers, representing parts of a whole. Understanding decimals is essential for many calculations and measurements, particularly in scientific and engineering applications where precision is paramount. The decimal point separates the whole number (7) from the fractional part (0.5). This allows for more precise representation of quantities that cannot be expressed as whole numbers.
Beyond the Basics: Exploring Further Mathematical Concepts
The seemingly simple problem of 15 divided by 2 opens the door to a wider understanding of several crucial mathematical concepts:
-
Rational Numbers: The result, 7.5, is a rational number – a number that can be expressed as a fraction (15/2). Understanding rational numbers is fundamental to algebra and calculus.
-
Real Numbers: 7.5 also belongs to the set of real numbers, encompassing both rational and irrational numbers. This broader classification is essential in advanced mathematical studies.
-
Modulo Operator: In computer science and programming, the modulo operator (%) provides the remainder of a division. 15 % 2 = 1, giving only the remainder. This operation is vital in many algorithms and computations.
Frequently Asked Questions (FAQ)
-
What is the remainder when 15 is divided by 2? The remainder is 1.
-
Can 15 be perfectly divided by 2? No, 15 cannot be perfectly divided by 2, resulting in a remainder.
-
What are the different ways to represent the answer? The answer can be represented as 7.5, 7 1/2, or as a fraction 15/2.
-
What is the significance of the decimal point in the answer 7.5? The decimal point separates the whole number (7) from the fractional part (0.5), representing a quantity that is not a whole number.
-
How is the concept of 15 divided by 2 applied in real life? It's applied in countless situations, from sharing items equally to scaling recipes, averaging data, and much more, as detailed in the Applications section above.
Conclusion: A Foundation for Further Learning
The seemingly simple calculation of 15 divided by 2 reveals a surprising depth and breadth of mathematical concepts and practical applications. From understanding quotients and remainders to grasping decimal representations and rational numbers, this basic division serves as a fundamental building block for more advanced mathematical explorations. By understanding the different methods of calculation and the various interpretations of the result, we can appreciate the importance of division in problem-solving across diverse fields. This deep dive demonstrates that even the simplest mathematical concepts can hold immense significance and serve as a gateway to a richer understanding of the world around us. It highlights the interconnectedness of mathematical concepts and emphasizes the importance of foundational knowledge in achieving mathematical fluency and problem-solving skills. The ability to dissect a problem like 15 divided by 2 and understand its various facets will empower you to tackle increasingly complex challenges in the future.
Latest Posts
Latest Posts
-
2 5 2
Sep 17, 2025
-
80 Of 35
Sep 17, 2025
-
1 72m In Feet
Sep 17, 2025
-
3 5 Of 240
Sep 17, 2025
-
Magnesium Sulphide Formula
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 15 Divided 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.