80 Of 35
stanleys
Sep 17, 2025 · 5 min read
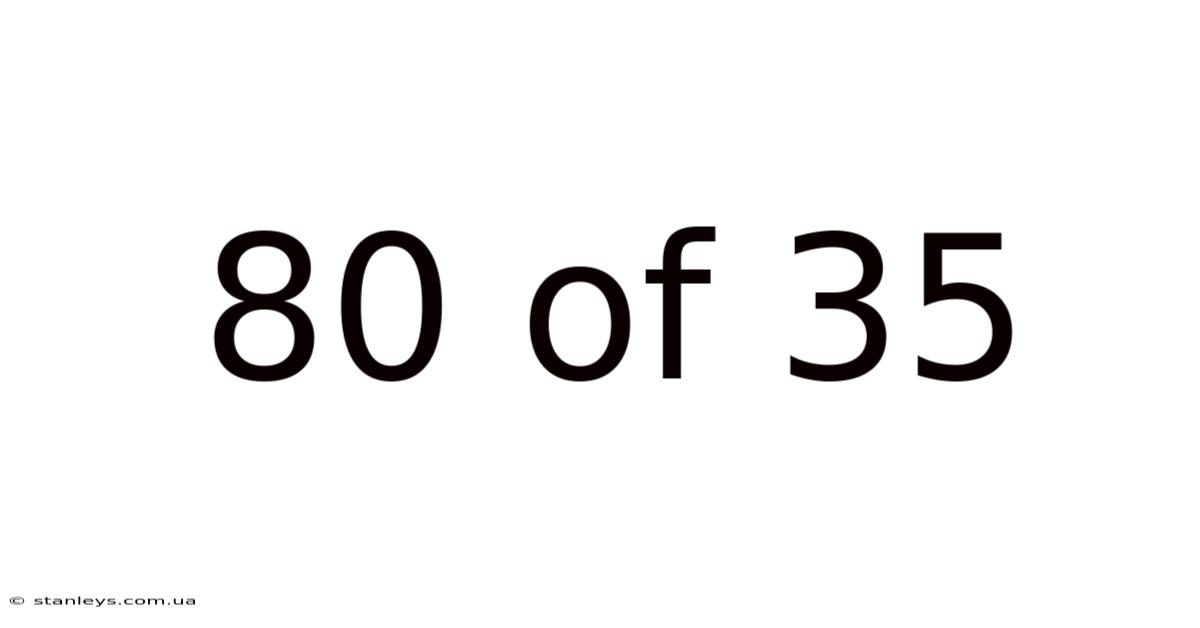
Table of Contents
Decoding 80 out of 35: Understanding Ratios and Proportions in a Real-World Context
Understanding ratios and proportions is fundamental to many aspects of life, from cooking and construction to finance and science. This article will delve deep into the seemingly unusual ratio of "80 out of 35," explaining what it means, how to interpret it, and its applications in various scenarios. We'll explore the mathematical concepts involved, discuss real-world examples, and address frequently asked questions to provide a comprehensive understanding. This exploration will go beyond simple calculation and illuminate the underlying principles of proportional reasoning.
Understanding the Basics: Ratios and Proportions
Before diving into the specifics of "80 out of 35," let's refresh our understanding of ratios and proportions. A ratio is a comparison of two or more quantities. It shows the relative size of one quantity to another. We often express ratios using a colon (:) or as a fraction. For instance, a ratio of 2:3 or 2/3 indicates that for every two units of one quantity, there are three units of another.
A proportion is a statement that two ratios are equal. It's a statement of equality between two ratios. Proportions are incredibly useful for solving problems involving scaling, comparing, and finding unknown quantities. For example, if the ratio of boys to girls in a class is 2:3, and there are 10 boys, we can set up a proportion to find the number of girls.
Interpreting "80 out of 35"
The phrase "80 out of 35" presents a ratio where the first number (80) represents a part or quantity, and the second number (35) represents the total. This ratio is improper, meaning the numerator (80) is larger than the denominator (35). This immediately suggests a few possible interpretations:
-
Beyond the Whole: This ratio likely represents a situation where the "part" (80) exceeds the "whole" (35). This isn't mathematically impossible; it simply indicates a context where the measured quantity surpasses the expected or initial total. This could arise from several scenarios, such as:
- Overachievement: Perhaps a target of 35 units was set, but 80 units were actually achieved, exceeding expectations.
- Growth or Increase: The initial quantity might have been 35, but subsequent growth resulted in a total of 80.
- Measurement Error: There might be an error in the initial measurement or reporting of the "total" quantity.
-
Multiple Sets: Another possibility is that this refers to multiple sets. For example, if we have multiple groups of 35, and in total, there are 80 items of interest across all the groups, this ratio would accurately reflect that situation.
Mathematical Representations and Calculations
We can represent "80 out of 35" in several ways:
- Fraction: 80/35
- Decimal: 80 ÷ 35 ≈ 2.29 (approximately)
- Percentage: (80/35) * 100% ≈ 228.57% (approximately)
The decimal and percentage representations offer different perspectives:
- Decimal (2.29): This shows that for every one unit of the initial quantity (35), there are approximately 2.29 units of the resulting quantity (80).
- Percentage (228.57%): This indicates that the final quantity (80) is approximately 228.57% of the initial quantity (35). This signifies a significant increase.
Real-World Examples
Let's explore how "80 out of 35" might appear in different contexts:
-
Production: A factory aimed to produce 35 units of a product per day, but due to increased efficiency, it actually produced 80 units. The ratio 80/35 reflects this overachievement.
-
Investment: An initial investment of $35,000 yielded a return of $80,000. The ratio 80/35 demonstrates a significant return on investment.
-
Growth: A population of 35 animals increased to 80 animals after a period of time. 80/35 shows the rate of population growth.
-
Surveys: A survey targeted 35 individuals, but 80 people responded. This ratio indicates a high response rate, exceeding the expected number of participants.
Simplifying the Ratio and Proportional Reasoning
While the ratio 80/35 stands as is in its given context, it can be simplified mathematically. Both 80 and 35 are divisible by 5, simplifying the ratio to 16/7. This simplified ratio maintains the proportional relationship; it still represents the same relative comparison between the two quantities. This simplified fraction (16/7) can be more easily interpreted in some contexts.
Applications of Proportional Reasoning
Understanding proportions allows us to solve various problems. For instance, if we know the ratio of ingredients in a recipe (e.g., 16 parts flour to 7 parts sugar), and we want to scale the recipe up or down, we can use this simplified ratio (16/7) and proportional reasoning to calculate the correct quantities of flour and sugar needed.
Frequently Asked Questions (FAQs)
-
Q: Is "80 out of 35" a valid ratio?
- A: Yes, while it's an improper fraction (numerator > denominator), it's a perfectly valid ratio representing a situation where the part exceeds the whole or involves multiple sets.
-
Q: How can I use this ratio in practical applications?
- A: The applications depend on the context. It can be used to calculate growth rates, compare achievements to targets, analyze survey results, or scale up/down recipes or production processes. The key is to understand the meaning of the numbers (part and total).
-
Q: What if the context makes the ratio illogical?
- A: If the context suggests the ratio shouldn't make sense (e.g., 80 apples from 35 apple trees, where one tree couldn't yield more than 1 apple) it likely indicates an error in the data collection or reporting. Carefully review the data source to identify any potential errors.
-
Q: How can I determine the best way to represent this ratio (fraction, decimal, percentage)?
- A: The best representation depends on the context. Percentages are good for communicating relative increases or decreases, while decimals are useful for calculations and precise comparisons. Fractions offer a clear representation of the parts-to-whole relationship.
Conclusion
The ratio "80 out of 35" is more than just a numerical expression; it represents a concept of proportional relationship where the part exceeds the initial whole. Understanding its mathematical implications and possible interpretations requires a grasp of ratios, proportions, and the ability to interpret them in real-world scenarios. This ratio emphasizes the importance of context in mathematical problem-solving. The ability to accurately interpret ratios like "80 out of 35" is a valuable skill applicable across diverse fields, improving problem-solving and decision-making capabilities. Remember to carefully analyze the context to understand the full implications of such ratios and choose the most appropriate method for representation and further calculations.
Latest Posts
Latest Posts
-
Pearl River Erskine
Sep 17, 2025
-
5 6 24
Sep 17, 2025
-
60 Of 32
Sep 17, 2025
-
127km In Miles
Sep 17, 2025
-
Patterns And Numbers
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 80 Of 35 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.