3/5 Of 240
stanleys
Sep 17, 2025 · 6 min read
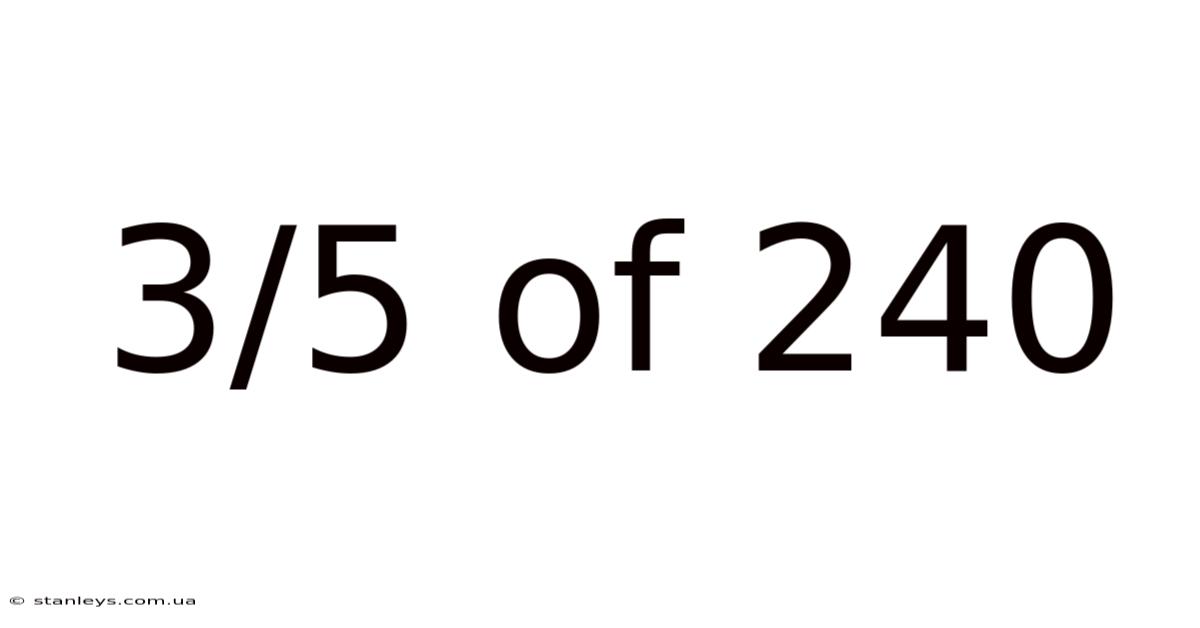
Table of Contents
Decoding 3/5 of 240: A Comprehensive Guide to Fractions and Proportions
Finding 3/5 of 240 might seem like a simple arithmetic problem, but it opens the door to a deeper understanding of fractions, proportions, and their applications in everyday life. This comprehensive guide will not only show you how to solve this specific problem but also equip you with the knowledge to tackle similar calculations with confidence. We'll explore different approaches, delve into the underlying mathematical concepts, and even touch upon real-world examples where this type of calculation is crucial.
Understanding Fractions: The Building Blocks
Before diving into the problem, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's written as a/b, where 'a' is the numerator (the part we're interested in) and 'b' is the denominator (the total number of parts). In our case, 3/5 represents three parts out of a total of five equal parts.
Different Methods to Calculate 3/5 of 240
There are several ways to calculate 3/5 of 240. Let's explore three common methods:
Method 1: Direct Multiplication
The most straightforward method is to multiply the fraction by the whole number. This involves converting the whole number into a fraction by placing it over 1:
(3/5) * (240/1) = (3 * 240) / (5 * 1) = 720 / 5 = 144
Therefore, 3/5 of 240 is 144.
Method 2: Finding One-Fifth and Multiplying
This method involves finding the value of one-fifth of 240 first, then multiplying that value by 3.
1/5 of 240 = 240 / 5 = 48
Since we need 3/5, we multiply 48 by 3:
48 * 3 = 144
Again, we arrive at the answer: 3/5 of 240 is 144. This method is particularly helpful when dealing with larger numbers or more complex fractions. It breaks down the problem into smaller, more manageable steps.
Method 3: Simplifying the Fraction First (If Possible)
Sometimes, you can simplify the fraction before performing the calculation. This makes the multiplication easier. However, in this case, 3/5 is already in its simplest form (the numerator and denominator share no common factors other than 1). This method is particularly useful when dealing with fractions that can be simplified, leading to smaller numbers and easier calculations.
Expanding the Concept: Proportions and Ratios
The calculation of 3/5 of 240 is fundamentally about proportions. A proportion is a statement that two ratios are equal. A ratio compares two quantities. In this case, we are comparing the part (3/5) to the whole (1). We can set up a proportion like this:
3/5 = x/240
To solve for x (which represents 3/5 of 240), we cross-multiply:
5x = 3 * 240 5x = 720 x = 720 / 5 x = 144
This method reinforces the concept of proportions and demonstrates how to solve for an unknown value in a proportional relationship. This is a crucial skill in various fields, including engineering, cooking, and even financial planning.
Real-World Applications: Where Fractions Matter
Understanding fractions and proportions is vital in numerous real-world scenarios:
-
Cooking and Baking: Recipes often use fractions (e.g., 1/2 cup of sugar, 2/3 cup of flour). Knowing how to calculate fractions is essential for accurate measurements and successful cooking. Imagine scaling up a recipe – understanding how to find a proportion of ingredients is crucial.
-
Construction and Engineering: Calculations in construction and engineering often rely heavily on fractions and ratios to ensure precise measurements and structural integrity. Think about calculating the amount of materials needed for a project based on blueprints that use fractional dimensions.
-
Finance and Budgeting: Percentages, which are simply fractions expressed out of 100, are fundamental in finance. Calculating interest, taxes, discounts, and investment returns all involve working with fractions. For example, calculating a 15% discount on an item involves finding 15/100 of the original price.
-
Data Analysis and Statistics: Fractions are essential for interpreting data and understanding statistical concepts like proportions and percentages. For instance, determining the percentage of respondents who prefer a particular product requires calculating a fraction based on the survey results.
-
Everyday Shopping: Determining the best value when comparing products with different sizes and prices often involves understanding and comparing unit prices, which essentially involve calculations with fractions.
Beyond the Basics: Further Exploration of Fractions
Let's delve a bit deeper into the world of fractions:
-
Equivalent Fractions: Different fractions can represent the same value. For instance, 3/5, 6/10, and 9/15 are all equivalent fractions. Simplifying fractions involves finding the equivalent fraction with the smallest possible numerator and denominator.
-
Improper Fractions and Mixed Numbers: An improper fraction has a numerator larger than or equal to the denominator (e.g., 7/5). A mixed number combines a whole number and a fraction (e.g., 1 2/5). Understanding how to convert between these forms is crucial for performing calculations.
-
Adding, Subtracting, Multiplying, and Dividing Fractions: Mastering these operations is fundamental to working with fractions confidently. Remember that adding and subtracting fractions require a common denominator, while multiplying fractions involves multiplying numerators and denominators separately, and dividing fractions involves inverting the second fraction and multiplying.
-
Decimal Representation of Fractions: Fractions can be expressed as decimals by dividing the numerator by the denominator. For example, 3/5 is equal to 0.6.
Frequently Asked Questions (FAQ)
Q: What if the fraction was something more complex, like 7/12 of 240?
A: You would follow the same principles. You can either use direct multiplication [(7/12) * (240/1)], find one-twelfth of 240 and multiply by 7, or simplify the fraction before calculating (if possible). In this case, 240 is divisible by 12, which simplifies the calculation.
Q: How can I improve my understanding of fractions?
A: Practice is key! Solve various problems involving fractions, starting with simpler ones and gradually increasing the complexity. Use visual aids like diagrams or pie charts to represent fractions, and utilize online resources or textbooks for extra support.
Q: Are there any online tools to help with fraction calculations?
A: Yes, many online calculators and websites are available to assist with fraction calculations, including those that explain the steps involved.
Q: What's the difference between a fraction and a decimal?
A: Both fractions and decimals represent parts of a whole. A fraction expresses a part as a ratio (numerator/denominator), while a decimal uses a base-ten system (e.g., 0.5 is equivalent to 1/2).
Conclusion: Mastering Fractions for a Brighter Future
Understanding how to calculate 3/5 of 240, and more broadly, mastering fractions and proportions, is not just about solving math problems; it's about developing crucial problem-solving skills applicable to various aspects of life. From everyday tasks to complex professional challenges, the ability to work with fractions confidently empowers you to make accurate calculations, solve problems efficiently, and make informed decisions. Remember that consistent practice and a willingness to explore different approaches are key to building a solid understanding of this fundamental mathematical concept. So, embrace the challenge, practice regularly, and unlock the power of fractions!
Latest Posts
Latest Posts
-
60 Of 32
Sep 17, 2025
-
127km In Miles
Sep 17, 2025
-
Patterns And Numbers
Sep 17, 2025
-
360g In Oz
Sep 17, 2025
-
Fire Extinguisher Symbol
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 3/5 Of 240 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.