132 Of 96
stanleys
Sep 10, 2025 · 5 min read
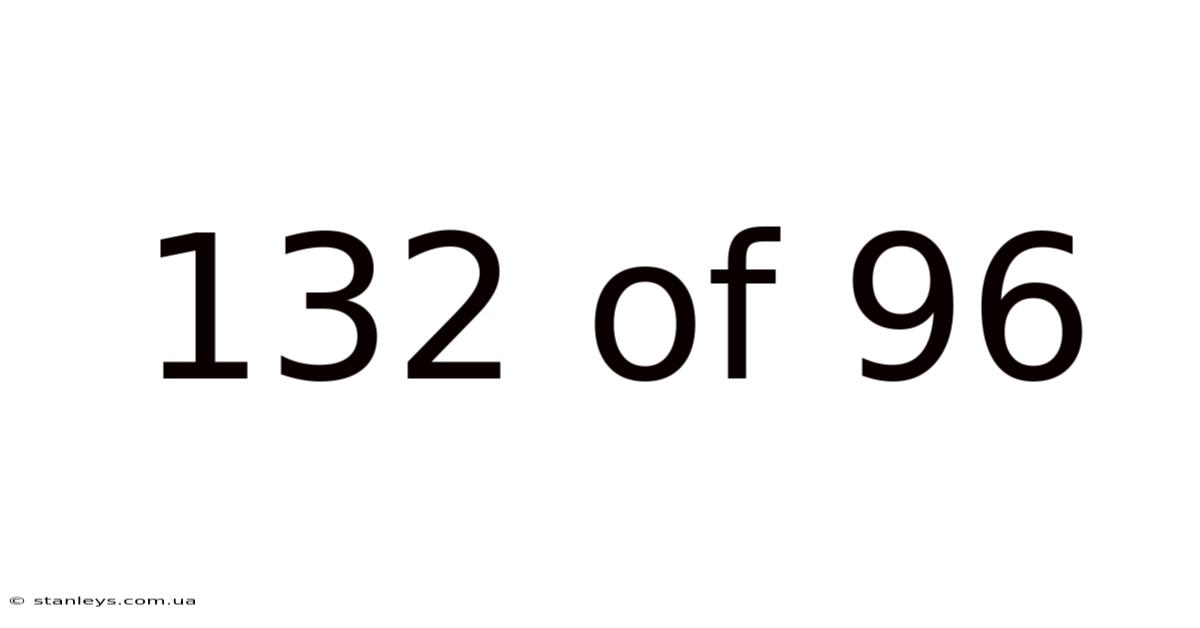
Table of Contents
Decoding the Mystery: Understanding 132 of 96 in the Context of Fractions, Ratios, and Percentages
This article delves into the seemingly simple yet multifaceted concept of "132 of 96." At first glance, it might appear illogical – how can you have 132 of something when you only started with 96? This seemingly paradoxical expression opens doors to explore fundamental mathematical concepts such as fractions, ratios, and percentages, revealing a deeper understanding of their application and interpretation. We’ll unpack this mystery, exploring various interpretations and demonstrating how context is crucial in determining its true meaning.
Understanding the Initial Paradox
The expression "132 of 96" immediately presents a challenge. It violates our basic understanding of whole numbers. You cannot have more than the total amount you started with. This initial apparent contradiction underscores the importance of considering the context within which such expressions are used. The numbers aren't necessarily representing whole, discrete units but might refer to parts of a whole, changes over time, or even represent different units entirely.
Interpretation 1: Percentage Increase or Decrease
One plausible interpretation is that "132 of 96" describes a percentage change. Perhaps 96 represents an initial value, and 132 represents a final value after an increase or, less likely, a negative value indicating a decrease (though that would be represented differently usually). To understand this, we need to calculate the percentage change:
- Percentage Change = [(Final Value - Initial Value) / Initial Value] x 100%
In this case:
- Percentage Change = [(132 - 96) / 96] x 100% = (36 / 96) x 100% = 0.375 x 100% = 37.5%
This interpretation suggests that the final value (132) is 37.5% greater than the initial value (96). This scenario is common in various contexts, such as:
- Financial Growth: A business might see a 37.5% increase in revenue from 96 units to 132 units.
- Population Increase: A town's population might grow by 37.5% from an initial population of 96 to a new population of 132.
- Data Analysis: An experiment might show a 37.5% increase in a particular measured variable.
Interpretation 2: Ratio or Proportion
Another interpretation views "132 of 96" as representing a ratio or proportion. The ratio 132:96 can be simplified by finding the greatest common divisor (GCD) of 132 and 96, which is 12. Simplifying the ratio, we get:
- 132:96 = (132/12) : (96/12) = 11:8
This ratio indicates that for every 8 units of one quantity, there are 11 units of another. This interpretation can apply to various situations, including:
- Recipe Ratios: A recipe might require a ratio of 11 parts of ingredient A to 8 parts of ingredient B.
- Mixing Solutions: A chemical solution might be created by combining 11 units of one substance with 8 units of another.
- Scale Models: A scale model might have a ratio of 11:8 in its dimensions.
Interpretation 3: Improper Fraction
"132 of 96" can also be interpreted as an improper fraction, representing 132/96. This fraction can be simplified by dividing both numerator and denominator by their GCD (12):
- 132/96 = (132/12) / (96/12) = 11/8
This improper fraction is equivalent to 1 and 3/8. This interpretation could arise in situations involving:
- Dividing Quantities: If 132 units are divided among 96 individuals, each individual would receive 11/8 units, or 1 and 3/8 units.
- Parts of a Whole: The fraction represents 132 parts of a whole that consists of 96 units. This is not typical usage, however.
Interpretation 4: Contextual Understanding as Crucial
The ambiguity of "132 of 96" highlights the vital role of context in interpreting mathematical expressions. Without knowing the specific situation, it's impossible to definitively determine the correct interpretation. The phrasing itself lacks the precision needed for unambiguous mathematical communication. Better phrasing would include units or a clear indication of the relationship between the numbers (e.g., "132 out of 96," "132 is what percent of 96?", "the ratio of 132 to 96").
Expanding the Understanding: Related Concepts
Understanding "132 of 96" requires a deeper comprehension of several interconnected mathematical concepts:
-
Fractions: The core element is the fractional representation 132/96, which can be simplified and converted to a mixed number or decimal. Understanding fraction simplification and their equivalence is essential.
-
Ratios: The ratio 132:96 represents a comparison of two quantities. Knowing how to simplify ratios and understand their implications in proportional relationships is crucial.
-
Percentages: The percentage change calculation involves converting a ratio to a percentage, which is a common method to express relative changes. Mastering percentage calculations is essential for interpreting data and understanding relative growth or decline.
-
Proportions: The concept of proportions underpins the ratio and percentage interpretations. Solving proportions is a vital skill in various mathematical applications.
-
Greatest Common Divisor (GCD): Finding the GCD is crucial for simplifying fractions and ratios. Understanding the methods for calculating the GCD is essential for mathematical fluency.
Frequently Asked Questions (FAQ)
-
Q: Can "132 of 96" be negative? A: Strictly speaking, no. A negative value would usually be expressed differently (e.g., a decrease of x%). However, within a specific context (like a net loss), it could represent a negative result.
-
Q: What is the most likely interpretation of "132 of 96"? A: There's no single most likely interpretation. The context is paramount. However, an increase/decrease percentage is a plausible interpretation if we consider the numbers to represent a change over time or an increase in some quantity.
-
Q: How can I improve the clarity of my mathematical expressions? A: Use precise language. Avoid ambiguity by clearly stating the units, the relationship between the numbers (using words like "of," "to," "out of," "percent of"), and the specific situation or context.
Conclusion: The Importance of Precision in Mathematics
The seemingly simple expression "132 of 96" serves as a powerful illustration of the importance of precise language and contextual understanding in mathematics. While the expression itself is ambiguous, analyzing it reveals fundamental concepts such as fractions, ratios, percentages, and proportions. This ambiguity underscores the need for clear communication in mathematics to avoid misinterpretations and ensure accurate calculations and conclusions. By understanding the various interpretations and their underlying principles, we can better appreciate the richness and complexity inherent in even the simplest mathematical expressions. The ability to analyze such ambiguities strengthens critical thinking and problem-solving skills vital in various fields, from finance and science to engineering and everyday life.
Latest Posts
Latest Posts
-
30 Of 210
Sep 11, 2025
-
40kilometers To Miles
Sep 11, 2025
-
75 Of 150
Sep 11, 2025
-
20 Of 65 00
Sep 11, 2025
-
76 1kg In Stone
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about 132 Of 96 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.