1000 / 25
stanleys
Sep 10, 2025 · 6 min read
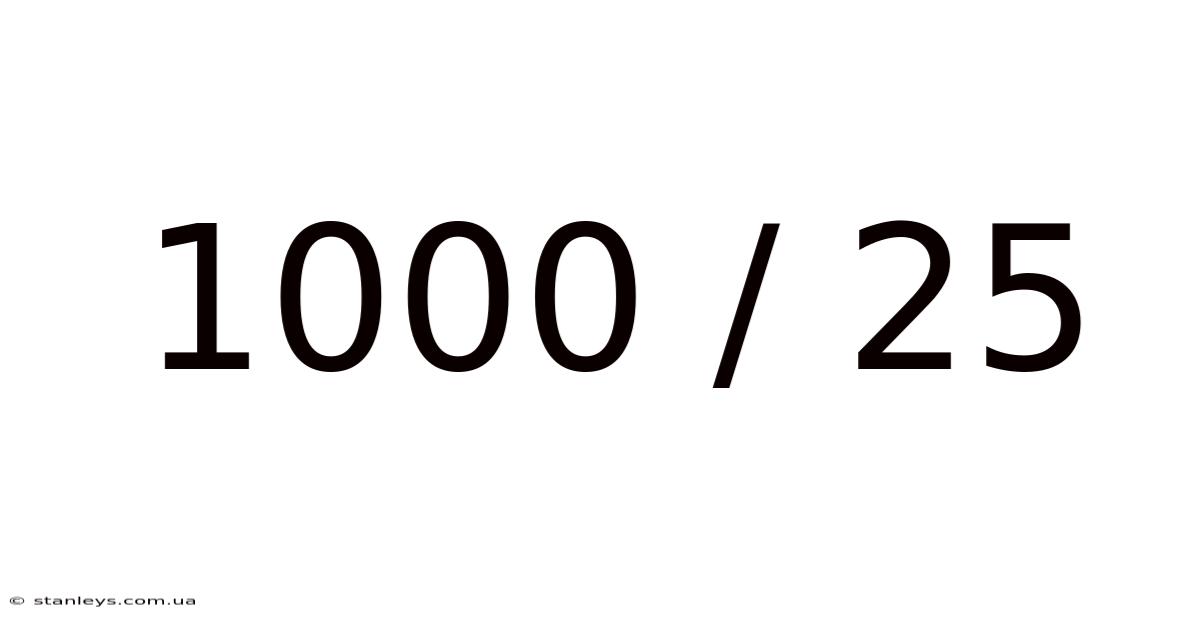
Table of Contents
Decoding 1000 / 25: A Deep Dive into Division and its Applications
This article explores the seemingly simple calculation of 1000 divided by 25, delving beyond the immediate answer to uncover the underlying mathematical principles and practical applications of division. We'll examine various methods for solving this problem, discuss the significance of division in different fields, and explore its role in everyday life. Understanding division, even a basic problem like 1000/25, opens doors to a wider comprehension of mathematics and its real-world relevance.
Introduction: The Fundamentals of Division
Division is one of the four basic arithmetic operations, alongside addition, subtraction, and multiplication. It represents the process of splitting a quantity into equal parts or determining how many times one number is contained within another. In the expression 1000 / 25, we're asking: "How many times does 25 fit into 1000?" The answer, as we'll see in multiple ways below, is 40. But understanding how to arrive at this answer is crucial.
Method 1: Long Division – A Classic Approach
Long division is a traditional method for performing division, particularly useful for larger numbers. It breaks down the division process into a series of steps, making it easier to manage. Here's how to solve 1000 / 25 using long division:
-
Set up the problem: Write 1000 as the dividend (the number being divided) and 25 as the divisor (the number dividing the dividend).
-
Divide the first digit(s): 25 doesn't go into 1, so we consider the first two digits, 10. 25 doesn't go into 10 either. We move to the first three digits, 100.
-
Estimate and subtract: 25 goes into 100 four times (4 x 25 = 100). Write the 4 above the 0 in 1000. Subtract 100 from 100, leaving 0.
-
Bring down the next digit: Bring down the next digit from the dividend (the last 0).
-
Repeat the process: We now have 00. 25 goes into 0 zero times. Write 0 above the last 0 in 1000. Subtract 0 from 0, leaving 0.
-
The quotient: The number at the top (40) is the quotient, representing the number of times 25 goes into 1000.
Therefore, 1000 / 25 = 40.
Method 2: Utilizing Multiplication – A Reverse Approach
Instead of long division, we can use our knowledge of multiplication tables to find the answer. We need to find a number that, when multiplied by 25, equals 1000. Thinking about multiples of 25, we know:
- 25 x 10 = 250
- 25 x 20 = 500
- 25 x 30 = 750
- 25 x 40 = 1000
Therefore, 1000 / 25 = 40. This method highlights the inverse relationship between multiplication and division.
Method 3: Simplifying Fractions – An Algebraic Perspective
We can express 1000 / 25 as a fraction: 1000/25. Fractions represent division. We can simplify this fraction by finding common factors between the numerator (1000) and the denominator (25). Both numbers are divisible by 25:
1000 ÷ 25 = 40 25 ÷ 25 = 1
So, 1000/25 simplifies to 40/1, which equals 40. This method showcases the equivalence between division and fraction simplification.
Method 4: Mental Math Techniques – Quick Calculations
For smaller numbers, mental math techniques can be highly efficient. Recognizing that 1000 is a multiple of 100, and 25 is a quarter of 100, we can use this relationship:
- 1000 is 10 times 100.
- 25 is 1/4 of 100.
- Therefore, 1000 / 25 is 10 x 4 = 40.
This demonstrates the power of recognizing patterns and utilizing mathematical relationships to perform quick calculations.
The Significance of Division in Various Fields
Division's application extends far beyond basic arithmetic. It's a fundamental concept in numerous fields:
-
Engineering and Physics: Division is crucial for calculations involving ratios, proportions, and rates. For example, calculating speed (distance/time), density (mass/volume), or force (pressure/area) all rely on division.
-
Finance and Economics: Dividing profit by investment helps determine the return on investment (ROI). Calculating average costs, interest rates, and shares all necessitate division.
-
Computer Science: Division plays a pivotal role in algorithms and programming. Data structures, hashing, and many other aspects depend on division operations.
-
Statistics: Calculating averages, medians, and standard deviations frequently involves division. Analyzing data and drawing conclusions often requires dividing datasets into groups or subgroups.
-
Everyday Life: Dividing a pizza among friends, splitting a bill, or calculating unit prices are common examples where division is used in daily life. Fair distribution and resource allocation inherently involve this fundamental mathematical operation.
Real-World Applications of 1000/25
The seemingly simple problem of 1000/25 has numerous real-world applications:
-
Inventory Management: If a warehouse has 1000 units of a product and each shipment contains 25 units, dividing 1000 by 25 tells us there are 40 shipments.
-
Resource Allocation: If a project requires 1000 man-hours and each worker contributes 25 man-hours, dividing 1000 by 25 indicates that 40 workers are needed.
-
Payment Calculations: If a total cost of $1000 is to be divided equally among 25 people, each person pays $40.
These scenarios highlight how understanding even a basic division problem like 1000/25 is directly applicable in solving practical problems across various contexts.
Frequently Asked Questions (FAQ)
-
Q: What if the dividend isn't a multiple of the divisor?
A: If the dividend isn't perfectly divisible by the divisor, you'll have a remainder. For instance, 1005 / 25 would result in a quotient of 40 with a remainder of 5. This remainder can be expressed as a fraction (5/25) or a decimal (0.2).
-
Q: Are there other ways to solve 1000 / 25?
A: Yes, various advanced mathematical techniques exist, such as using logarithms or computational tools. However, for this specific problem, the methods outlined above are the most efficient and accessible.
-
Q: Why is understanding division important?
A: Division is a cornerstone of mathematics, with applications across numerous disciplines. Understanding division builds a strong foundation for more advanced mathematical concepts and problem-solving skills.
-
Q: How can I improve my division skills?
A: Practice is key! Start with simpler problems and gradually increase the complexity. Use different methods to solve the same problem, and focus on understanding the underlying concepts.
Conclusion: The Enduring Power of Division
The seemingly simple calculation of 1000 / 25 reveals a wealth of mathematical concepts and practical applications. By exploring various methods and examining its significance in different fields, we gain a deeper appreciation for the fundamental role division plays in our understanding and interaction with the world around us. Mastering division isn't just about getting the right answer; it's about developing crucial problem-solving skills and expanding mathematical intuition. The ability to efficiently and accurately perform division – from simple problems like 1000/25 to more complex calculations – is a valuable asset in both academic pursuits and real-world scenarios. Through practice and understanding, the power of division becomes readily apparent.
Latest Posts
Latest Posts
-
0 85 To Fraction
Sep 11, 2025
-
30 Of 210
Sep 11, 2025
-
40kilometers To Miles
Sep 11, 2025
-
75 Of 150
Sep 11, 2025
-
20 Of 65 00
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about 1000 / 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.