X3 X 3
stanleys
Sep 14, 2025 · 5 min read
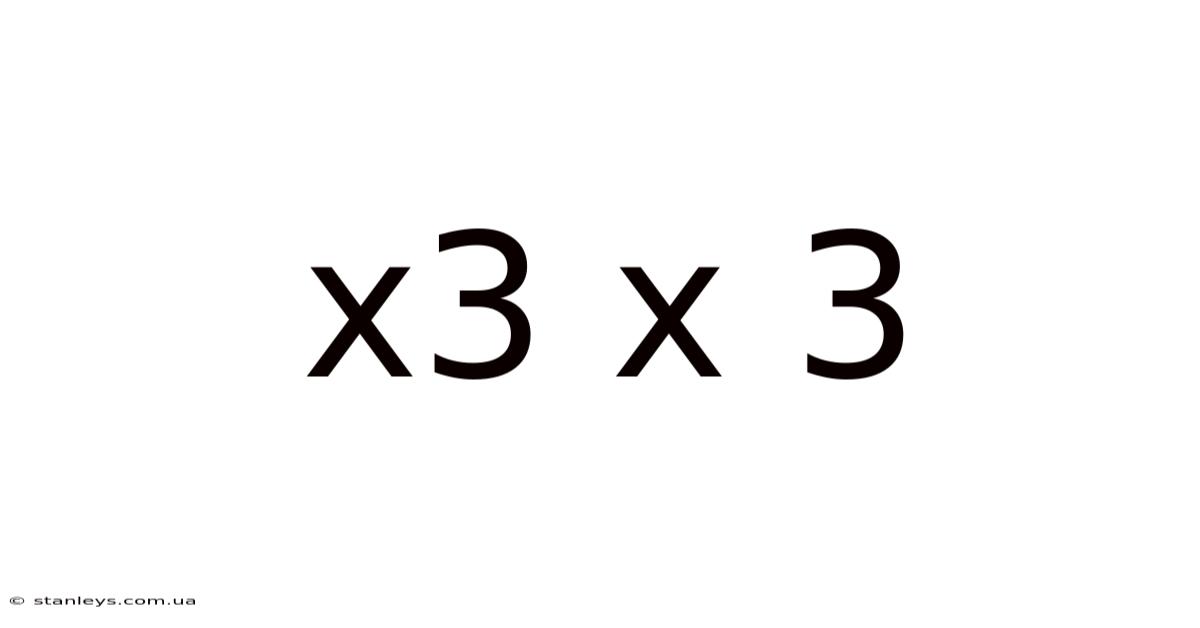
Table of Contents
Decoding the Mystery of X³ x 3: Exploring Cubic Equations and Beyond
This article delves into the mathematical expression "x³ x 3," exploring its meaning, applications, and the broader mathematical concepts it embodies. We'll unpack the fundamentals of cubic equations, their solutions, and the significance of this specific expression in various mathematical contexts. Understanding this seemingly simple expression opens doors to a deeper appreciation of algebra and its powerful applications in diverse fields.
Introduction: Understanding the Basics
At first glance, "x³ x 3" appears straightforward. It represents the product of a cubic term (x cubed, or x raised to the power of 3) and the constant 3. Mathematically, it's written as 3x³. However, this simple expression acts as a gateway to a wealth of mathematical concepts, including:
-
Cubic Equations: Understanding 3x³ involves grasping the nature of cubic equations, which are polynomial equations of degree three. These equations have the general form ax³ + bx² + cx + d = 0, where a, b, c, and d are constants, and a ≠ 0. Our expression, 3x³, forms a part of such equations.
-
Polynomials: The expression is a monomial, a single term within a polynomial. Polynomials are sums of monomials, and mastering polynomials is fundamental to algebra and calculus.
-
Functions: The expression 3x³ can be viewed as a function, f(x) = 3x³, where the input x is cubed and then multiplied by 3, producing the output f(x). This function has its own graph, properties, and applications.
-
Derivatives and Integrals (Calculus): In calculus, this expression's derivative (the instantaneous rate of change) and integral (the area under the curve) are easily calculated, revealing further mathematical properties and applications.
Solving Cubic Equations: Methods and Techniques
While our specific expression 3x³ doesn't constitute a complete cubic equation (it lacks the x², x, and constant terms), understanding how to solve cubic equations is crucial to comprehending its place within a larger mathematical context. Several methods exist for solving cubic equations, including:
-
Factoring: If a cubic equation can be factored, finding its roots becomes significantly simpler. This usually involves identifying common factors or using techniques like the rational root theorem to find potential rational roots.
-
The Cubic Formula: Similar to the quadratic formula for solving quadratic equations, a more complex cubic formula exists to find the roots of a cubic equation. This formula, however, is considerably more intricate and less practical for hand calculations.
-
Numerical Methods: For cubic equations that are difficult or impossible to solve analytically (using formulas), numerical methods like the Newton-Raphson method provide approximate solutions. These methods involve iterative processes to refine estimates of the roots.
-
Graphical Methods: Plotting the cubic function graphically can help visually identify the roots (x-intercepts) of the equation. This method offers a visual understanding of the equation's behavior and its solutions.
The Significance of 3x³ in Various Contexts
The expression 3x³ appears in various mathematical contexts, impacting different areas of study:
-
Volume Calculations: In geometry, 3x³ could represent the volume of a cube with side length x, multiplied by a constant factor of 3. This could model scenarios involving multiple cubes or a scaled-up version of a single cube.
-
Physics and Engineering: Cubic relationships often appear in physics and engineering, describing phenomena such as the volume of a fluid, the displacement of a spring, or the power output of a device. 3x³ could be a simplified model of such relationships, incorporating a scaling factor.
-
Economics and Finance: Cubic functions can model complex economic phenomena, such as production functions or cost-benefit analyses. The expression 3x³ could be a component of such models, representing a specific contribution to the overall function.
-
Computer Science and Data Structures: The time complexity of certain algorithms can be expressed using cubic functions. The expression 3x³ could indicate the algorithm's efficiency, showing how processing time scales with input size (x).
Expanding the Understanding: Related Concepts
To fully grasp the implications of 3x³, let's explore related mathematical concepts:
-
Higher-Order Polynomials: Cubic equations are a subset of higher-order polynomial equations (quartic, quintic, etc.). Understanding cubic equations provides a foundational understanding for tackling these more complex polynomial expressions.
-
Partial Fractions: In calculus and algebra, complex rational functions can be simplified using partial fraction decomposition. This process often involves working with cubic expressions in the denominator.
-
Taylor and Maclaurin Series: These powerful series approximations represent functions as infinite sums of simpler terms. Cubic expressions often form part of these series, providing accurate approximations of more complicated functions.
-
Differential Equations: Cubic expressions frequently appear in differential equations, which model dynamic systems in physics, engineering, and other fields. Solving these equations often requires understanding cubic functions and their properties.
Frequently Asked Questions (FAQ)
-
Q: What is the derivative of 3x³?
- A: The derivative of 3x³ with respect to x is 9x².
-
Q: What is the integral of 3x³?
- A: The indefinite integral of 3x³ with respect to x is (3/4)x⁴ + C, where C is the constant of integration.
-
Q: How do I solve the equation 3x³ = 27?
- A: Divide both sides by 3 to get x³ = 9. Then take the cube root of both sides to find x = ∛9 (approximately 2.08).
-
Q: Can 3x³ ever be negative?
- A: Yes, if x is a negative number, then 3x³ will be negative. For example, if x = -2, then 3x³ = 3(-8) = -24.
-
Q: What is the significance of the coefficient 3 in 3x³?
- A: The coefficient 3 acts as a scaling factor. It stretches or compresses the graph of the function x³ vertically.
Conclusion: The Broader Implications of a Simple Expression
The expression "x³ x 3," or 3x³, while seemingly simple, unlocks a deeper understanding of cubic equations, polynomials, functions, and their applications in diverse fields. By exploring its mathematical properties, solving related equations, and examining its context within broader mathematical frameworks, we gain a much richer appreciation for the power and elegance of algebraic concepts. From geometry to calculus, from physics to economics, the significance of this seemingly straightforward expression extends far beyond its initial appearance, demonstrating the interconnectedness and far-reaching impact of fundamental mathematical principles. Continuing to explore these concepts will further refine your mathematical understanding and equip you with valuable tools for problem-solving and critical thinking in various academic and professional pursuits.
Latest Posts
Latest Posts
-
Pink To Yellow
Sep 14, 2025
-
Disadvantages Of Ssd
Sep 14, 2025
-
49 4kg In Stone
Sep 14, 2025
-
107cm In Ft
Sep 14, 2025
-
70 Of 400
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about X3 X 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.