X 3x 2
stanleys
Sep 16, 2025 · 6 min read
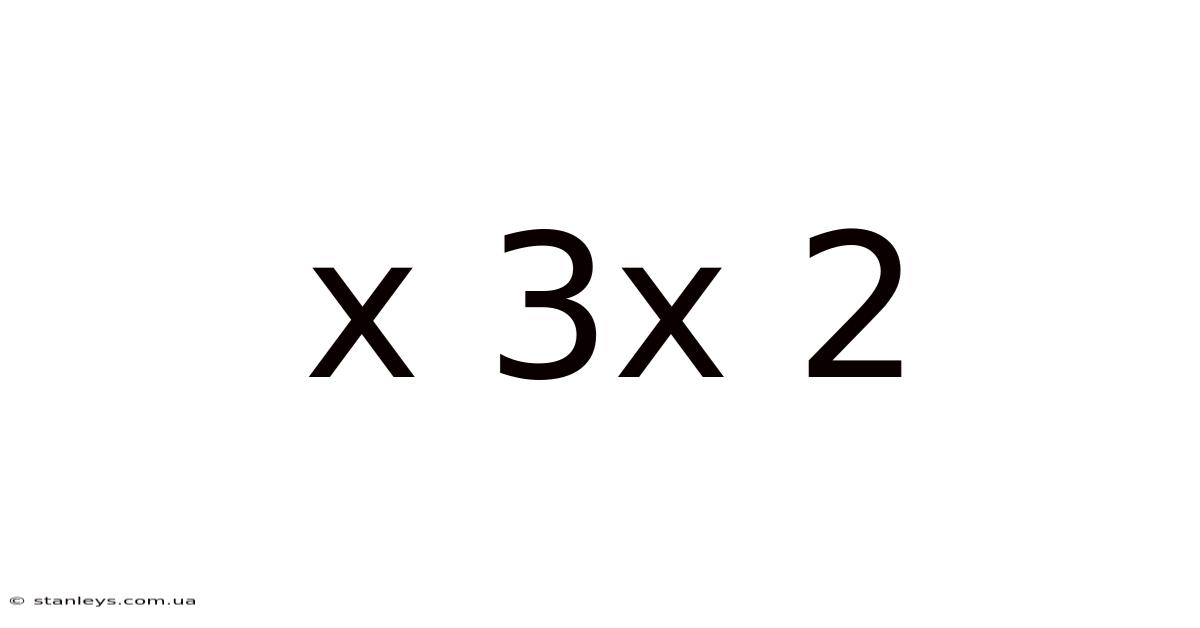
Table of Contents
Decoding the Mystery: Exploring the Mathematical Relationship of x, 3x, and 2
This article delves into the mathematical relationship between the variables x, 3x, and the constant 2. We'll explore various scenarios where these elements appear, demonstrating how understanding their interplay can unlock solutions in algebra, geometry, and even real-world problem-solving. Whether you're a student grappling with algebraic equations or simply curious about the elegance of mathematical relationships, this comprehensive guide will equip you with a deeper understanding of this seemingly simple yet versatile concept.
Introduction: Understanding the Fundamentals
At first glance, the expressions x, 3x, and 2 might seem unrelated. However, understanding their connections forms a crucial foundation for numerous mathematical concepts. The key lies in recognizing that x represents an unknown value, while 3x signifies a multiple of that unknown value, and 2 is a constant. The relationship between them hinges on the operations performed and the context in which they appear.
1. Solving Equations Involving x, 3x, and 2
One common application involves solving algebraic equations. Let's explore a few examples:
- Example 1: x + 3x = 2
This equation is a simple linear equation. To solve for x, we first combine like terms:
4x = 2
Then, we divide both sides by 4:
x = 2/4 = 1/2 or 0.5
Therefore, the solution to the equation x + 3x = 2 is x = 0.5.
- Example 2: 3x - 2 = x
This equation requires a slightly different approach. We start by isolating the 'x' terms on one side of the equation and the constant terms on the other:
3x - x = 2
2x = 2
x = 1
The solution to the equation 3x - 2 = x is x = 1.
- Example 3: x² + 3x - 2 = 0
This equation introduces a quadratic term (x²). Solving quadratic equations often requires using the quadratic formula:
x = (-b ± √(b² - 4ac)) / 2a
Where a, b, and c are coefficients of the quadratic equation ax² + bx + c = 0. In this case, a = 1, b = 3, and c = -2. Plugging these values into the quadratic formula will yield two solutions for x.
x = (-3 ± √(3² - 4 * 1 * -2)) / (2 * 1) x = (-3 ± √(17)) / 2
This results in two approximate solutions: x ≈ 0.56 and x ≈ -3.56
2. Geometric Interpretations
The relationship between x, 3x, and 2 can also be visualized geometrically. Imagine scenarios involving lengths, areas, or volumes:
- Scenario 1: Lengths of Sides
Consider a rectangle where one side has length x and the other side has length 3x. The perimeter of this rectangle would be 2(x + 3x) = 8x. If the perimeter is known to be 2 units (2 = 8x), then we can solve for x (x = 2/8 = 1/4). This shows how the relationship between x and 3x directly impacts the geometric properties of the shape.
- Scenario 2: Area of a Triangle
Suppose the base of a triangle is 3x and its height is 2. The area of the triangle (1/2 * base * height) would be (1/2) * 3x * 2 = 3x. If the area is known, we can solve for x. For example, if the area is 6 square units, then 3x = 6, leading to x = 2.
3. Real-world Applications
The expressions x, 3x, and 2 are not confined to abstract mathematical exercises. They frequently appear in real-world problem-solving scenarios:
- Example 1: Cost and Profit
Imagine a business where the cost of producing one item is x dollars. The cost of producing three items would be 3x dollars. If the profit from selling three items is $2, the equation could be represented as 3x + 2 = total revenue. This enables calculating the cost per item (x) based on total revenue.
- Example 2: Distance, Speed, and Time
Consider a scenario involving travel. If a car travels at a speed of x km/h for 3 hours, the total distance covered would be 3x km. If this distance is 2 km less than the planned distance, we can form an equation to find the speed (x).
- Example 3: Mixture Problems
In chemistry or cooking, mixture problems often involve ratios. Imagine mixing a solution where the concentration of one component is x%, and another component is 3x%. If the total volume of the mixture is 2 liters, we can use this information to find the volume and concentration of each component.
4. Expanding the Concept: Inequalities
The relationship between x, 3x, and 2 can also be explored using inequalities. For example:
-
x + 3x > 2 This inequality implies that the sum of x and 3x is greater than 2. Solving this inequality yields x > 1/2.
-
3x - 2 < x This inequality states that 3x minus 2 is less than x. Solving it reveals x < 1.
Understanding inequalities is crucial for analyzing ranges of possible values for x within a given context.
5. Advanced Applications: Calculus and Beyond
The simple relationship between x, 3x, and 2 forms a foundation for more advanced mathematical concepts. In calculus, for instance, the derivative of 3x is simply 3, a constant rate of change. This constant rate highlights the linear relationship between x and 3x. In more complex scenarios involving functions, derivatives, and integrals, understanding this fundamental relationship allows for more efficient problem-solving.
Frequently Asked Questions (FAQ)
-
Q: What if 2 is replaced by another constant? A: The same principles apply. The solution will simply adjust according to the new constant value. The methodology for solving the equation remains consistent.
-
Q: Can x be a negative number? A: Yes, x can be negative. The solution to the equations involving x, 3x, and 2 can result in a negative value for x, depending on the specific equation.
-
Q: What if there are more variables involved? A: If more variables are introduced, the complexity increases, requiring more sophisticated techniques such as simultaneous equations or matrix operations to solve for all the unknown variables.
-
Q: Are there limitations to this approach? A: While versatile, this approach primarily deals with linear and quadratic equations. For higher-order polynomial equations or transcendental equations, more advanced techniques are necessary.
Conclusion: The Power of Simplicity
The seemingly simple relationship between x, 3x, and 2 possesses far-reaching implications. Understanding their interplay unlocks problem-solving capabilities across various mathematical domains and real-world applications. By mastering the fundamentals of solving equations, interpreting geometric representations, and applying this knowledge to real-world scenarios, you gain a powerful tool for tackling complex challenges and deepening your mathematical understanding. From elementary algebra to advanced calculus, the foundation laid by grasping this fundamental relationship is crucial for continued mathematical growth. Remember, mathematics is not just about numbers; it's about understanding the relationships and connections between them, and this exploration provides a perfect illustration of that principle.
Latest Posts
Related Post
Thank you for visiting our website which covers about X 3x 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.